顶点覆盖问题的近似算法

问题描述：无向图G=(V,E)的顶点覆盖是它的顶点集V的一个子集V’包含于V，使得若(u,v)是G的一条边，则v∈V’或u∈V’。顶点覆盖V’的大小是它所包含的顶点个数|V’|。

下面的近似算法以无向图G为输入，并计算出G的近似最优顶点覆盖，可以保证计算出的近似最优顶点覆盖大小不会超过最小顶点覆盖大小的2倍。

VertexSet approxVertexCover ( Graph g )

{ cset=空集；

e1=g.e；

while (e1 != 空集) {

从e1中任取一条边(u,v)；

cset=cset∪{u,v}；

从e1中删去与u和v相关联的所有边；

}

return c

}

Cset用来存储顶点覆盖中的各顶点。初始为空，不断从边集e1中选取一边(u,v)，将边的端点加入cset中，并将e1中已被u和v覆盖的边删去，直至cset已覆盖所有边。即e1为空。

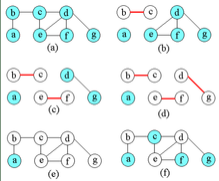
图(a)～(e)说明了算法的运行过程及结果。(e)表示算法产生的近似最优顶点覆盖cset，它由顶点b,c,d,e,f,g所组成。(f)是图G的一个最小顶点覆盖，它只含有3个顶点：b,d和e。

下面考察近似算法的性能。若用A记为算法循环中选取出的边的集合，则A中任何两条边没有公共顶点。算法终止时有|cset|=2|A|.

另一方面，图G的任一顶点覆盖，一定包含A中各边的至少一个端顶点，G的最小顶点覆盖也不例外。因此，若最小顶点覆盖为cset*,则｜cset*|>=A.由此可得，｜cset|<=2|cset*|.即算法的性能比为2.

以下参考北大屈老师课件：

 

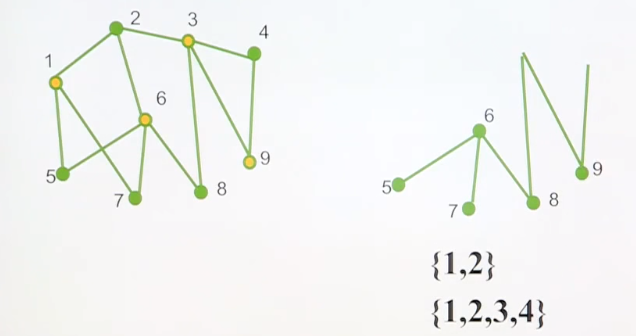
 对于上图，我们来运行下近似算法。比如我们任意选择一条边，比如说1和2关联的边。

 选了之后，覆盖集含有1和2两个顶点，然后删除与1和2顶点关联的边

 再次选择3，4顶点，然后3，4顶点进入覆盖集。

 删除与3，4顶点关联的边。

 重复上述步骤，此时选择5，6顶点。

 

 近似算法输出1，2，3，4，5，6.但最优解是1，3，6，9.故近似算法有误差。

 

 

 

 参考：王晓东《算法设计与分析》第二版

           北大《算法设计与分析第二版》

           https://baike.so.com/doc/5688800-5901497.html