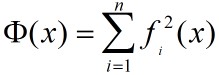数值概率算法
1、用随机投点法计算pi值
设有一半径为r的圆及其外切四边形。向该正方形随机地投掷n个点。设落入圆内的点数为k。由于所投入的点在正方形上均匀分布,因而所投入的点落入圆内的概率为(PI * pow(r,2)) / (4 * pow(r,2)) = PI / 4 。所以当n足够大时,k与n之比就逼近这一概率。从而,PI 约等于 (4*k)/n.如下图:

实现:

#include <iostream> #include <cstdlib> #include <limits> using namespace std; // 获得0-1之间的随机数 double get_random_num () { return (double)rand () / RAND_MAX ; } // 用随机投点法计算 PI double darts (int n) { int k = 0 ; for (int i = 0; i < n; ++ i) { double x = get_random_num() ; double y = get_random_num() ; if ((x * x + y * y) <= 1.0) { ++ k ; } } return (4 * k) / (double)n ; } int main() { cout << darts (200000000) << endl ; }
实现结果:
2.计算定积分
设f(x)是[0,1]上的连续函数,且0 <= f(x) <= 1。
需要计算的积分为![]() ,积分I等于图中的面积G。
,积分I等于图中的面积G。

在图所示单位正方形内均匀地作投点试验,则随机点落在曲线下面的概率为
![]()
假设向单位正方形内随机地投入n个点(xi,yi)。如果有m个点落入
G内,则随机点落入G内的概率![]()
假定 f(x) = x * x (0 <= x <= 1)计算定积分
实现:

#include <iostream> #include <cstdlib> using namespace std; // 获得0-1之间的随机数 double get_random_num () { return (double)rand () / RAND_MAX ; } // 用随机投点法计算 y = pow(x,2)定积分 double darts (int n) { int k = 0 ; for (int i = 0; i < n; ++ i) { double x = get_random_num() ; double y = get_random_num() ; if (y <= x * x) { ++ k ; } } return k / (double)n ; } int main() { cout << darts (10000000) << endl ; return 0; }
运行结果:
3.解非线性方程组
求解下面的非线性方程组
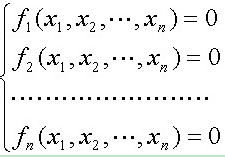
其中,x1,x2,…,xn是实变量,fi是未知量x1,x2,…,xn的非线性实函数。要求确定上述方程组在指定求根范围内的一组解
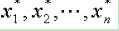
问题分析
解决这类问题有多种数值方法,如:牛顿法、拟牛顿法、粒子群算法等。最常用的有线性化方法和求函数极小值方法。为了求解所给的非线性方程组,构造一目标函数
式中,x=(x1,x2,……xn)。易知,函数取得零点即是所求非线性方程组的一组解。
求解思路
在指定求根区域D内,选定一个随机点x0作为随机搜索的出发点。在算法的搜索过程中,假设第j步随机搜索得到的随机搜索点为xj。在第j+1步,计算出下一步的随机搜索增量dxj。从当前点xj依dxj得到第j+1步的随机搜索点。当x<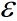
实现:

//随机化算法 解线性方程组 #include "stdafx.h" #include "RandomNumber.h" #include <iostream> using namespace std; bool NonLinear(double *x0,double *dx0,double *x,double a0, double epsilon,double k,int n,int Steps,int M); double f(double *x,int n); int main() { double *x0, //根初值 *x, //根 *dx0, //增量初值 a0 = 0.0001, //步长 epsilon = 0.01, //精度 k = 1.1; //步长变参 int n = 2, //方程个数 Steps = 10000, //执行次数 M = 1000; //失败次数 x0 = new double[n+1]; dx0 = new double[n+1]; x = new double[n+1]; //根初值 x0[1] = 0.0; x0[2] = 0.0; //增量初值 dx0[1] = 0.01; dx0[2] = 0.01; cout<<"原方程组为:"<<endl; cout<<"x1-x2=1"<<endl; cout<<"x1+x2=3"<<endl; cout<<"此方程租的根为:"<<endl; bool flag = NonLinear(x0,dx0,x,a0,epsilon,k,n,Steps,M); while(!flag) { flag = NonLinear(x0,dx0,x,a0,epsilon,k,n,Steps,M); } for(int i=1; i<=n; i++) { cout<<"x"<<i<<"="<<x[i]<<" "; } cout<<endl; return 0; } //解非线性方程组的随机化算法 bool NonLinear(double *x0,double *dx0,double *x,double a0, double epsilon,double k,int n,int Steps,int M) { static RandomNumber rnd; bool success; //搜索成功标志 double *dx,*r; dx = new double[n+1]; //步进增量向量 r = new double[n+1]; //搜索方向向量 int mm = 0; //当前搜索失败次数 int j = 0; //迭代次数 double a = a0; //步长因子 for(int i=1; i<=n; i++) { x[i] = x0[i]; dx[i] = dx0[i]; } double fx = f(x,n); //计算目标函数值 double min = fx; //当前最优值 while(j<Steps) { //(1)计算随机搜索步长 if(fx<min)//搜索成功 { min = fx; a *= k; success = true; } else//搜索失败 { mm++; if(mm>M) { a /= k; } success = false; } if(min<epsilon) { break; } //(2)计算随机搜索方向和增量 for(int i=1; i<=n; i++) { r[i] = 2.0 * rnd.fRandom()-1; } if(success) { for(int i=1; i<=n; i++) { dx[i] = a * r[i]; } } else { for(int i=1; i<=n; i++) { dx[i] = a * r[i] - dx[i]; } } //(3)计算随机搜索点 for(int i=1; i<=n; i++) { x[i] += dx[i]; } //(4)计算目标函数值 fx = f(x,n); j++; } if(fx<=epsilon) { return true; } else { return false; } } double f(double *x,int n) { return (x[1]-x[2]-1)*(x[1]-x[2]-1) +(x[1]+x[2]-3)*(x[1]+x[2]-3); }
运行结果:
参考:王晓东《算法设计与分析》第二版
https://www.cnblogs.com/chinazhangjie/archive/2010/11/11/1874924.html