回溯法之圆排列问题
问题描述
给定n个大小不等的圆c1,c2,…,cn,现要将这n个圆排进一个矩形框中,且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如,当n=3,且所给的3个圆的半径分别为1,1,2时,这3个圆的最小长度的圆排列如图所示。其最小长度为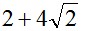
问题分析
圆排列问题的解空间是一棵排列树。按照回溯法搜索排列树的算法框架,设开始时a=[r1,r2,……rn]是所给的n个元的半径,则相应的排列树由a[1:n]的所有排列构成。
解圆排列问题的回溯算法中,CirclePerm(n,a)返回找到的最小的圆排列长度。初始时,数组a是输入的n个圆的半径,计算结束后返回相应于最优解的圆排列。center计算圆在当前圆排列中的横坐标,由x^2 = sqrt((r1+r2)^2-(r1-r2)^2)推导出x = 2*sqrt(r1*r2)。Compoute计算当前圆排列的长度。变量min记录当前最小圆排列长度。数组r表示当前圆排列。数组x则记录当前圆排列中各圆的圆心横坐标。
在递归算法Backtrack中,当i>n时,算法搜索至叶节点,得到新的圆排列方案。此时算法调用Compute计算当前圆排列的长度,适时更新当前最优值。
当i<n时,当前扩展节点位于排列树的i-1层。此时算法选择下一个要排列的圆,并计算相应的下界函数。
算法具体代码如下:

//圆排列问题 回溯法求解 #include "stdafx.h" #include <iostream> #include <cmath> using namespace std; float CirclePerm(int n,float *a); template <class Type> inline void Swap(Type &a, Type &b); int main() { float *a = new float[4]; a[1] = 1,a[2] = 1,a[3] = 2; cout<<"圆排列中各圆的半径分别为:"<<endl; for(int i=1; i<4; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"最小圆排列长度为:"; cout<<CirclePerm(3,a)<<endl; return 0; } class Circle { friend float CirclePerm(int,float *); private: float Center(int t);//计算当前所选择的圆在当前圆排列中圆心的横坐标 void Compute();//计算当前圆排列的长度 void Backtrack(int t); float min, //当前最优值 *x, //当前圆排列圆心横坐标 *r; //当前圆排列 int n; //圆排列中圆的个数 }; // 计算当前所选择圆的圆心横坐标 float Circle::Center(int t) { float temp=0; for (int j=1;j<t;j++) { //由x^2 = sqrt((r1+r2)^2-(r1-r2)^2)推导而来 float valuex=x[j]+2.0*sqrt(r[t]*r[j]); if (valuex>temp) { temp=valuex; } } return temp; } // 计算当前圆排列的长度 void Circle::Compute(void) { float low=0,high=0; for (int i=1;i<=n;i++) { if (x[i]-r[i]<low) { low=x[i]-r[i]; } if (x[i]+r[i]>high) { high=x[i]+r[i]; } } if (high-low<min) { min=high-low; } } void Circle::Backtrack(int t) { if (t>n) { Compute(); } else { for (int j = t; j <= n; j++) { Swap(r[t], r[j]); float centerx=Center(t); if (centerx+r[t]+r[1]<min)//下界约束 { x[t]=centerx; Backtrack(t+1); } Swap(r[t], r[j]); } } } float CirclePerm(int n,float *a) { Circle X; X.n = n; X.r = a; X.min = 100000; float *x = new float[n+1]; X.x = x; X.Backtrack(1); delete []x; return X.min; } template <class Type> inline void Swap(Type &a, Type &b) { Type temp=a; a=b; b=temp; }
运行结果
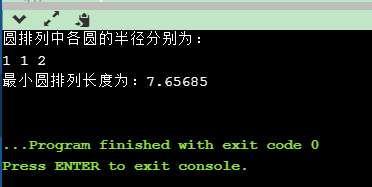
算法效率
如果不考虑计算当前圆排列中各圆的圆心横坐标和计算当前圆排列长度所需的计算时间按,则 Backtrack需要O(n!)计算时间。由于算法Backtrack在最坏情况下需要计算O(n!)次圆排列长度,每次计算需要O(n)计算时间,从而整个算法的计算时间复杂性为O((n+1)!)
上述算法尚有许多改进的余地。例如,像1,2,…,n-1,n和n,n-1, …,2,1这种互为镜像的排列具有相同的圆排列长度,只计算一个就够了,可减少约一半的计算量。另一方面,如果所给的n个圆中有k个圆有相同的半径,则这k个圆产生的k!个完全相同的圆排列,只计算一个就够了。
参考文献:王晓东《算法设计与分析》
https://blog.csdn.net/liufeng_king/article/details/8890603