回溯法之装载问题

问题描述：

    一共有n个货物要装上两艘重量分别为c1和c2的轮船上，其中货物i的重量为Wi，且：

                        

    要求确定是否有一个合理的装载方案可将货物装上这两艘轮船。

采取策略：      
 (1)首先将第一艘轮船尽可能装满；
 (2)将剩余的集装箱装上第二艘轮船。将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，
     使该子集中集装箱重量之和最接近。由此可知，装载问题等价于以下特殊的0-1背包问题：

                              

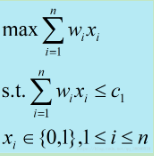
算法设计：

　　先考虑装载一艘轮船的情况，依次讨论每个集装箱的装载情况，共分为两种，要么装(1)，要么不装(0)，因此很明显其解空间树可以用子集树来表示。

　　在算法Maxloading中，返回不超过c的最大子集和，但是并没有给出到达这个最大子集和的相应子集，稍后完善。

　　在算法Maxloading中，调用递归函数Backtrack(1)实现回溯搜索。Backtrack(i)搜索子集树中的第i层子树。

　　在算法Backtrack中，当i>n时，算法搜索到叶结点，其相应的载重量为cw，如果cw>bestw，则表示当前解优于当前的最优解，此时应该更新bestw。

　　算法Backtrack动态地生成问题的解空间树。在每个结点处算法花费O(1)时间。子集树中结点个数为O(2^n)，故Backtrack所需的时间为O(2^n)。另外Backtrack还需要额外的O(n)的递归栈空间。

代码实现：

#include <iostream>
using namespace std;
 
typedef int* pINT;
template<class Type>
class Loading{
public:
    friend Type MaxLoading(Type* w,int num ,Type C1,int* bestx );
    friend void SolveLoading(int C2,bool* x,int* w,int num);
 
    void Backtrack(int i);
 
    int num;/* 集装箱数目 */
    int * x;/* 当前解 */
    int * bestx;/* 当前最优解 */
 
    Type* w;/* 集装箱重量数组 */
    Type  C1;/* 第一艘船的容量 */
    Type cw;
    Type bestw;
    Type r;/* 剩余集装箱重量 */
};
 
template<class Type>
void Loading<Type>::Backtrack( int i )
{
    if( i > num){
        if ( cw > bestw ) {
            for (int i = 1; i <= num ; i++ ) {
                bestx[i] = x[i];
                bestw = cw;                
            }
        }
        return ;
    }
    r -= w[i];
    if ( cw+w[i] <= C1 ) {
        x[i] = 1;
        cw += w[i];
        Backtrack(i+1);
        cw -= w[i];
    }
 
    if ( cw+r > bestw ) {
        x[i] = 0;
        Backtrack(i+1);
    }
 
    r += w[i];
 
}
template<class Type>
 Type   MaxLoading( Type* w,int num ,Type C1,int* bestx )
{
    Loading<Type> X;
    X.x = new int[num+1];
    X.w = w;
    X.C1= C1;
    X.num = num;
    X.bestx = bestx;
    X.bestw = 0;
    X.cw = 0;
    X.r = 0;
    for (int i = 1; i <= num ; i++ ) {
        X.r += w[i];
    }
    X.Backtrack(1);
    delete[] X.x;
    return X.bestw;
 
}
template<class Type>
 void    SolveLoading( int C2,int* x,Type* w,int num )
 {
     int totalW = 0;
     int c1W = 0;/* 第一艘船总载重 */
     for (int i = 1; i <= num ; i++ ) {
         if ( x[i] == 1 ) {
             c1W += w[i];
         } 
         totalW += w[i];
     }
     if ( totalW-c1W > C2 ) {
         printf("没有合理的装载方案! :( ");
         return;
     }
 
     printf(" 装载方案如下:\n ");
     printf(" 第一艘船装 ");
     for (int i = 1; i <= num ; i++ ) {
         if ( x[i] == 1 ) {
             printf("%d ",i);
         } 
     }
     printf("\n总载重 %d \n",c1W);
 
 
     printf(" 第二艘船装 ");
     for (int i = 1; i <= num ; i++ ) {
         if ( ! x[i] ) {
             printf("%d ",i);
         } 
     }
     printf("\n总载重 %d \n",totalW-c1W);
 
}
 
int main(int argc,char* argv[]){
 
    int C1 = 0;
    int C2 = 0;
    int num = 0;
    int* x = NULL;
    int** m = NULL;
    int* w = NULL;
 
    printf("输入第一艘船最大载重量:");
    scanf("%d",&C1);
 
    printf("输入第二艘船最大载重量:");
    scanf("%d",&C2);
 
 
    printf("输入货物个数");
    scanf("%d",&num);
 
    x = new int[num+1];
    w = new int[num+1];
    m = new pINT[num+1];
    for (int i = 0; i < num+1 ; i++ ) {
        m[i] = new int[num+1];
    }
 
 
    printf("分别输入货物重量（回车结束）：\n");
 
    for (int i = 1; i <= num ; i++ ) {
        scanf("%d",w+i);
    }
 
 
 
    MaxLoading(  w, num, C1, x );
 
    SolveLoading(C2, x, w, num);
 
    delete[] x;
    delete[] w;
    delete[] m;
    
    return 0;
}
 

实现结果:

参考：王晓东《算法设计与分析》第二版

          https://www.cnblogs.com/xymqx/p/3724356.html