贪心法之最优装载问题

概念：

当一个问题具有最优子结构性质时，可用动态规划算法，有时会有更简单有效的算法，那就是贪心算法，贪心算法是通过一系列的选择来得到问题的解，贪心算法并不从整体最优上加以考虑，所做的选择只是在某种意义上的局部最优解。但对范围相当广的许多问题能产生整体最优解。在一些情况下，即使贪心算法不能得到整体最优解，但其最终结果却是最优解的很好的近似解。

贪心算法的基本要素：

贪心选择性质：所求解的问题的整体最优解可以通过一系列局部最优的选择来，即贪心选择达到。贪心选择所依赖的是以前所做过的选择，而对以后所做的选择没有关系。

最优子结构性质：一个问题的最优解包含其子问题的最优解。

贪心算法与动态规划的区别：

动态规划是通过自底向上的方式解决子问题，贪心算法是通过自顶向下的迭代方式做出贪心选择，求解问题的最优解。两共同点是都具有最优子结构性质。

---

最优装载问题：某艘船的载重量为C，每件物品的重量为wi,要将尽量多的物品装入到船上。

分析：贪心策略：每次都选择最轻的，然后再从剩下的n-1件物品中选择最轻的。

算法策略：把n件物品 从小到大排序，然后根据贪心策略尽可能多的选出前i个物品，直到不能装为止。

这个问题比部分背包问题还简单，先拿轻的再拿重的可以保证最后物品装的最多。代码如下：

#include<iostream>
#include<algorithm>
#define MAXN 10000
using namespace std;
int main(){
    int c,n;    //c:船的最高载重量 n:古董数量
    int sum=0,weight=0; //sum:装入的古董数量 weight:装入的古董重量
    int w[MAXN];    //单个古董对应的重量
    cout<<"请输入最高载重量和需载的古董数目："<<endl;
    cin>>c>>n;
    cout<<"请分别输入这些古董的重量:"<<endl;
    for(int i=1;i<=n;++i)
        cin>>w[i];
    sort(w+1,w+1+n);
    for(int i = 1 ; i<=n ; i++){
        weight += w[i]; //先将重量加进去
        if(weight >= c){
            if(weight == c)   //恰好装满时
                sum = i;
            else
                sum = i-1;  //超重了，需要减去一个
            break;
        }
    }
    cout<<"最多可以装"<<sum<<"个"<<endl;
    for(int i=1;i<=sum;++i)
        cout<<w[i]<<" ";
    return 0;
}

程序运行结果：

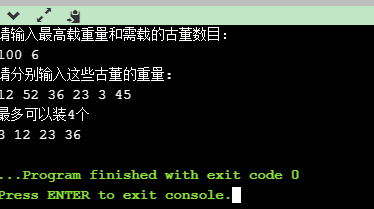
 参考：王晓东《算法设计与分析》

            https://blog.csdn.net/qq648483997/article/details/93309028