动态规划(DP)之多边形游戏问题
问题描述:
多边形游戏是一个单人玩的游戏,开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值,每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。
游戏第1步,将一条边删除。
随后n-1步按以下方式操作:
(1)选择一条边E以及由E连接着的2个顶点V1和V2;
(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。
最后,所有边都被删除,游戏结束。游戏的得分就是所剩顶点上的整数值。
问题:对于给定的多边形,计算最高得分。
如下图:
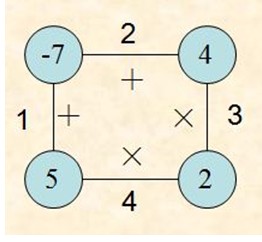
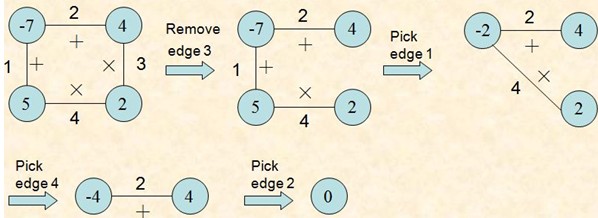
数据输入:
第一行是一个整数N
第二行按照
边 顶点 边 顶点 …. 边 顶点
的顺序以此存放了N个顶点和N条边的标注信息。
问题求解:
当把一条边去除除后,再把它拉直,那么这个问题就可以变成一条链。那么就和以前写的矩阵连乘有几分的相似,其实我们最后要求的是这个链的表达式算式结果的最大值。于是我们就可以想到可以用数组p[i][j]来表示从点i开始,链长为j的算术表达式的最大值,用v[i]存储操作数,op[i]存储操作符。如果这条链的最后一次合并运算在op[i+s]处发生(1≤s≤j-1),则可在op[i+s]处将链分割为2个子链p[i][s]和p[i+s][j-s]。似乎这样再按照以前解决动态规划题目时的思路,就可以解决问题了。 但是,我们再来考虑一下,由于有两种运算符+和x,并且操作数可能存在负数,那么我们也必须考虑两个负数相乘的结果可能比两个正数要打,所以我们同时还需要记录每个链的最大和最小值,然后判断,如果操作符为+的话,只需要两个链的最大值相加即可,如果操作符是x的话,那么必须把各种情况考虑进来,然后再求出最大值。分析如下:
(1)当op[i+s]='+'时,显然有a+c≤m≤b+d
(2)当op[i+s]='*'时,由于v[i]可取负整数,子链的最大值相乘未必能得到主链的最大值,但是注意到最大值一定在边界点取到,有min{ac,ad,bc,bd}≤m≤max{ac,ad,bc,bd}
换句话说,主链的最大值和最小值可由子链的最大值和最小值得到。例如,当m=ac时,最大主链由它的两条最小子链组成;同理当m=bd时,最大主链由它的两条最大子链组成
问题分析:
解决该问题可用动态规划中的最优子结构性质来解。
设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中,op[i]表示第i条边所对应的运算符,v[i]表示第i个顶点上的数值,i=1~n。
在所给的多边形中,从顶点i(1<=i<=n)开始,长度为j(链中有j个顶点)的顺时针链p(i,j)可表示为v[i],op[i+1],…,v[i+j-1],如果这条链的最后一次合并运算在op[i+s]处发生(1<=s<=j-1),则可在op[i+s]处将链分割为两个子链p(i,s)和p(i+s,j-s)。
设m[i,j,0]是链p(i,j)合并的最小值,而m[i,j,1]是最大值。若最优合并在op[i+s]处将p(i,j)分为两个长度小于j的子链的最大值和最小值均已计算出。即:
a=m[i,i+s,0] b=m[i,i+s,1] c=m[i+s,j-s,0] d=m[i+s,j-s,1]
(1) 当op[i+s]=’+’时
m[i,j,0]=a+c ;m[i,j,1]=b+d
(2) 当op[i+s]=’*’时
m[i,j,0]=min{ac,ad,bc,bd} ; m[i,j,1]=max{ac,ad,bc,bd}
综合(1)和(2),将p(i,j)在op[i+s]处断开的最大值记为maxf(i,j,s)最小值记为minf(i,j,s),则
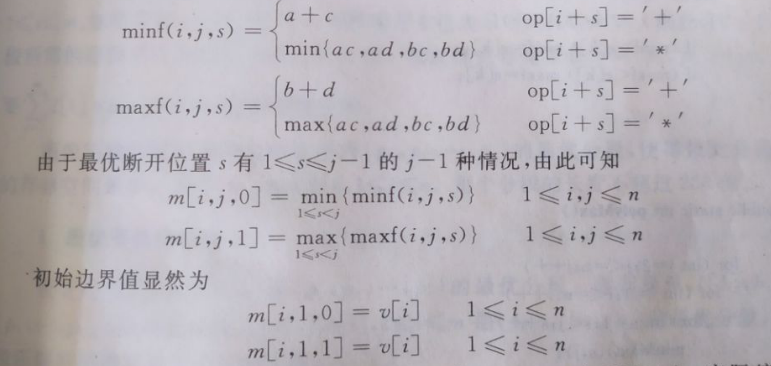
由于最优断开位置s有1<=s<=j-1的j-1中情况。 初始边界值为 m[i,1,0]=v[i] 1<=i<=n m[i,1,1]=v[i] 1<=i<=n
因为多变形式封闭的,在上面的计算中,当i+s>n时,顶点i+s实际编号为(i+s)modn。按上述递推式计算出的m[i,n,1]记为游戏首次删除第i条边后得到的最大得分。
代码实现:
#include<string.h> #include<stdio.h> int v[101]; int n; char op[101]; int minf,maxf; int m[101][101][2]; void minMax(int i,int s,int j) { int e[5]; int a=m[i][s][0], b=m[i][s][1], r=(i+s-1)%n+1, c=m[r][j-s][0], d=m[r][j-s][1]; if(op[r]=='t') { minf=a+c; maxf=b+d; } else { e[1]=a*c; e[2]=a*d; e[3]=b*c; e[4]=b*d; minf=e[1]; maxf=e[1]; for(int k=2; k<5; k++) { if(minf>e[k]) minf=e[k]; if(maxf<e[k]) maxf=e[k]; } } } int main() { memset(m,0,sizeof(m)); scanf("%d",&n); getchar(); for(int i=1; i<=n; i++) { scanf("%c",&op[i]); scanf("%d",&v[i]); m[i][1][0]=v[i]; m[i][1][1]=v[i]; getchar(); } for(int j=2; j<=n; j++)//链的长度 for(int i=1; i<=n; i++)//删掉第i条边 for(int s=1; s<j; s++)//断开的位置 { minMax(i,s,j); if(m[i][j][0]>minf) m[i][j][0]=minf; if(m[i][j][1]<maxf) m[i][j][1]=maxf; } int temp=m[1][n][1]; for(int i=2; i<=n; i++) { if(temp<m[i][n][1]) temp=m[i][n][1]; } printf("%d\n",temp); return 0; }
结果输出:
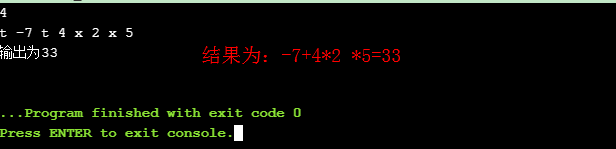
(由程序输出可见初始时删除的边为序号1)
参考文献:王晓东《算法设计与分析》



