Sigmoid和Softmax和Softplus
1、什么是 softmax
机器学习总归是要接触到 softmax 的，那么这个东东倒底是怎么来的呢？对于熟悉机器学习或神经网络的读者来说，sigmoid与softmax两个激活函数并不陌生，但这两个激活函数在逻辑回归中应用，也是面试和笔试会问到的一些内容，掌握好这两个激活函数及其衍生的能力是很基础且重要的，下面为大家介绍下这两类激活函数。当然激活函数不仅仅是以上两种，还有线性函数，tanh函数，hard tanh函数，修正线性函数（Leaky ReLU,softpus(ReLU的平滑版本)）----更多见Deep Learning：A Practitioner's Approach中文版
1.1. softmax function
这函数定义比较符合 softmax 这个名字：
可见 softmax function 是从一个输入序列里算出一个值。
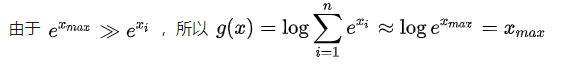
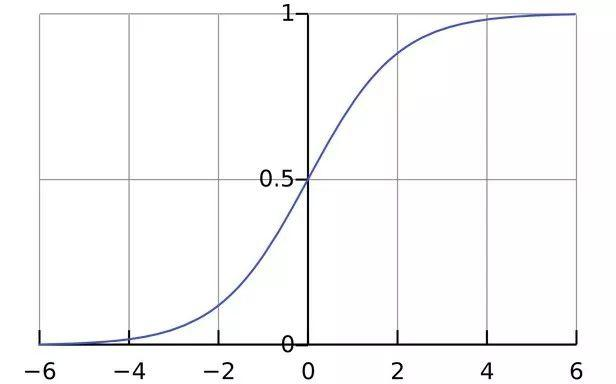
可见 softmax 确实会返回输入序列中最大的那个值的近似值。softmax 是对真 max 函数的近似，softmax 的函数曲线是光滑的（处处可微分），而 max(0,x) 之类的函数则会有折点。
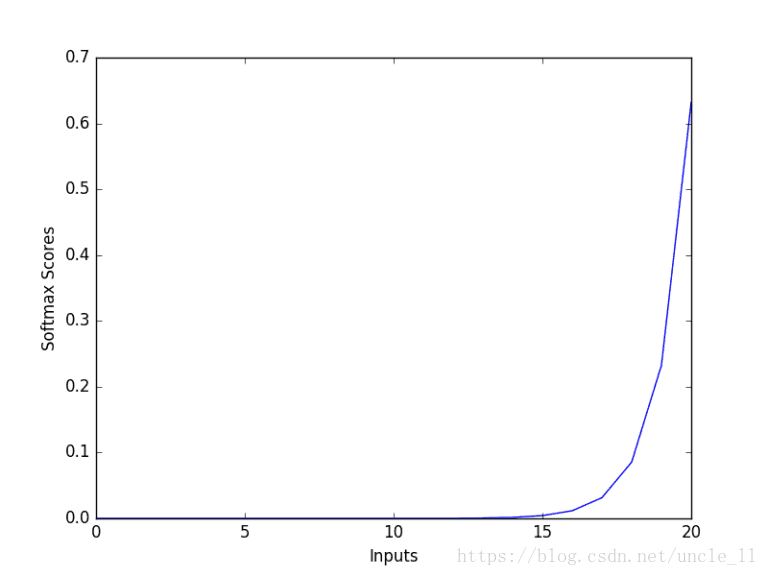
上图（图片来源网络）显示了softmax函数的基本属性，输入值越大，其概率越高。
在机器学习领域，多分类算法需要从一组可能的结果中找出概率最高的那个，正需要使用 max 函数。而为了能进行优化，用于描述问题的函数必须是可微分的，这样 softmax 就是一个非常合适的选择了。
1.2. softmax activation function
这是机器学习领域广为使用的一个函数，也叫 归一化指数函数，它的定义是：
可见 softmax activation function 返回的是一个序列，这个函数的分母部分跟 softmax function 有一部分是相同的，并且在效果上也有一点儿相似：通过运算会扩大最大项的优势并抑制序列中其余的项。
能在互联网上查到的记录显示，1989 年 John S. Bridle 在论文“Probabilistic Interpretation of Feedforward Classification Network Outputs, with relationships to statistical pattern recognition” 中首次引入了 softmax activation function 。这位 2013 年加入苹果至今，在搞 Siri 。
这个函数能够将输入序列的每一个值挤压到[0,1]范围内，并且所有项的和为1。因为这个特性，概率论用它的输出结果表达类别分布。
*-*：softmax函数的本质就是将一个K维的任意实数向量压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0，1）之间。
在机器学习领域也用它来整理分类算法的结果，multinomial logistic regression (多元逻辑回归)、Linear discriminant analysis(线性判别分析)、naive Bayes classifiers(朴素贝叶斯分类器)、人工神经网络都可以用。
2、Sigmoid和Softmax用于分类
设计模型执行分类任务（如对胸部X光检查到的疾病或手写数字进行分类）时，有时需要同时选择多个答案（如同时选择肺炎和脓肿），有时只能选择一个答案（如数字“8”）。下面将讨论如何应用Sigmoid函数或Softmax函数处理分类器的原始输出值。
2.1神经网络分类器
分类算法有很多种，但本文讨论的内容只限于神经网络分类器。分类问题可通过不同神经网络进行解决，如前馈神经网络和卷积神经网络。
2.2应用Sigmoid函数或Softmax函数
神经网络分类器最终结果为某一向量，即“原始输出值”，如[-0.5, 1.2, -0.1, 2.4]，这四个输出值分别对应胸部X光检查后发现的肺炎、心脏肥大、瘤和脓肿。但这些原始输出值是什么意思？
将输出值转换为概率可能更容易理解。比起看似随意的“2.4”，患有糖尿病的可能性为91％，这种说法更便于患者理解。
Sigmoid函数或Softmax函数可以将分类器的原始输出值映射为概率。(一般根据神经网络设置最终输出是实值输出则为回归，输出一组概率则为分类)
下图显示了将前馈神经网络的原始输出值（蓝色）通过Sigmoid函数映射为概率（红色）的过程：
然后采用Softmax函数重复上述过程：
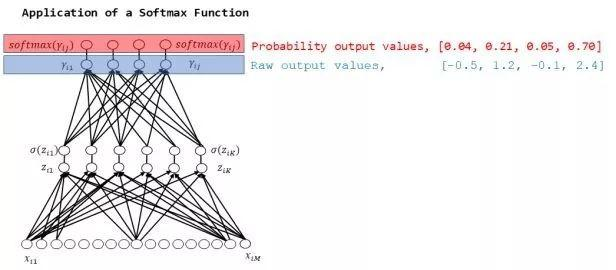
如图所示，Sigmoid函数和Softmax函数得出不同结果。
原因在于，Sigmoid函数会分别处理各个原始输出值，因此其结果相互独立，概率总和不一定为1，如图0.37 + 0.77 + 0.48 + 0.91 = 2.53。
相反，Softmax函数的输出值相互关联，其概率的总和始终为1，如图0.04 + 0.21 + 0.05 + 0.70 = 1.00。因此，在Softmax函数中，为增大某一类别的概率，其他类别的概率必须相应减少。
3、Sigmoid函数应用：
3.1以胸部X光检查和入院为例
胸部X光片：一张胸部X光片能够同时显示多种疾病，因此胸部X射线分类器也需要同时显示多种病征。下图为一张显示肺炎和脓肿的胸部X光片，在右侧的标签栏中有两个“1”：
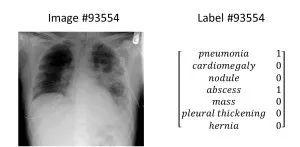
入院：目标是根据患者的健康档案，判断该患者将来入院的可能性。因此，分类问题可设计为：根据诊断可能导致患者未来入院的病症（如果有的话），对该患者现有的健康档案进行分类。导致患者入院的疾病可能有多种，因此答案可能有多个。
图表：下面两个前馈神经网络分别对应上述问题。在最后计算中，由Sigmoid函数处理原始输出值，得出相应概率，允许多种可能性并存——因胸部X射线可能反映出多种异常状态，则患者入院的病因可能不止一种。
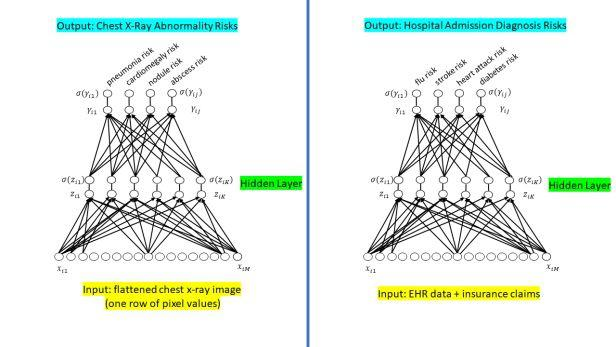
4.Softmax函数应用：
4.1以手写数字和Iris（鸢尾花）为例
手写数字：在区别手写数字时，分类器应采用Softmax函数，明确数字为哪一类。毕竟，数字8只能是数字8，不能同时是数字7。
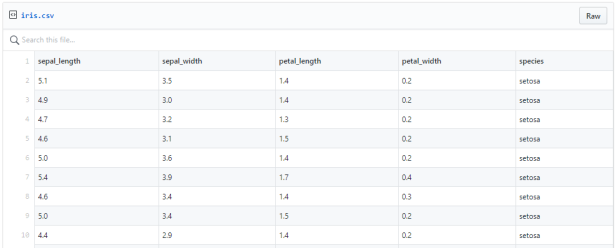
Iris：Iris数据集于1936年引入，一共包含150个数据集，分为山鸢尾、杂色鸢尾、维吉尼亚鸢尾3类，每类各有50个数据集，每个数据包含花萼长度、花萼宽度、花瓣长度、花瓣宽度4个属性。
以下9个示例摘自Iris数据集：
数据集中没有任何图像，但下图的杂色鸢尾，可供你欣赏：
Iris数据集的神经网络分类器，要采用Softmax函数处理原始输出值，因为一朵鸢尾花只能是某一个特定品种——将其分为几个品种毫无意义。
4.2关于“e”的注解
要理解Sigmoid和Softmax函数，应先引入 “e”。在本文中，只需了解e是约等于2.71828的数学常数。
下面是关于e的其他信息：
e的十进制表示永远存在，数字出现完全随机——类似于pi。
e常用于复利、赌博和某些概率分布的研究中。
下面是e的一个公式：
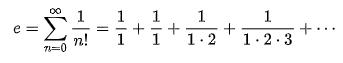
但e的公式不止一个。其计算方法有多种。
2004年，谷歌公司首次公开募股达2,718,281,828美元，即“e百万美元”。
维基百科中人类历史上著名的十进制数字e的演变，从1690年的一位数字开始，持续到1978年的116,000位数字：
5.Sigmoid函数和Softmax函数
5.1Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）
构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值。
Sigmoid函数如下所示（注意e）：
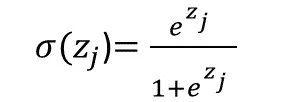
在该公式中，σ表示Sigmoid函数，σ（zj）表示将Sigmoid函数应用于数字Zj。 “Zj”表示单个原始输出值，如-0.5。 j表示当前运算的输出值。如果有四个原始输出值，则j = 1,2,3或4。在前面的例子中，原始输出值为[-0.5,1.2，-0.1,2.4]，则Z1 = -0.5，Z2 = 1.2，Z3 = -0.1，Z4 = 2.4。
所以，
Z2，Z3、Z4 的计算过程同上。
由于Sigmoid函数分别应用于每个原始输出值，因此可能出现的输出情况包括：所有类别概率都很低（如“此胸部X光检查没有异常”），一种类别的概率很高但是其他类别的概率很低（如“胸部X光检查仅发现肺炎”），多个或所有类别的概率都很高（如“胸部X光检查发现肺炎和脓肿”）。
下图为Sigmoid函数曲线：
5.2Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）
构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。
Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。
Softmax函数表述如下：
除分母外，为综合所有因素，将原始输出值中的e ^ thing相加，Softmax函数与Sigmoid函数差别不大。换言之，用Softmax函数计算单个原始输出值（例如Z1）时，不能只计算Z1，分母中的Z1，Z2，Z3和Z4也应加以计算，如下所示：
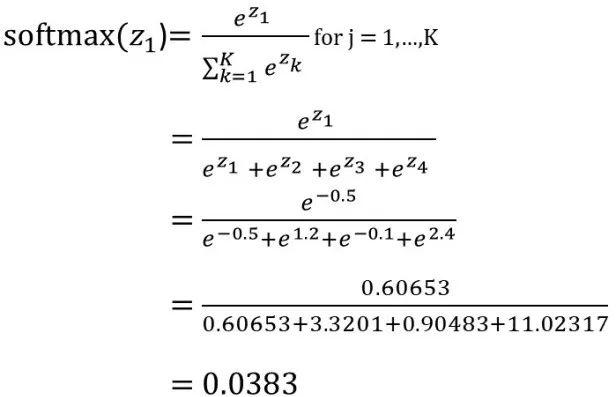
Softmax函数的优势在于所有输出概率的总和为1：
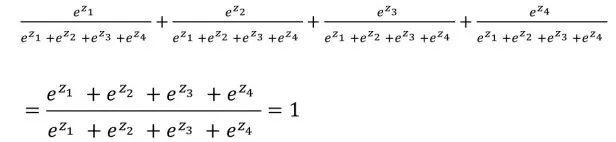
区分手写数字时，用Softmax函数处理原始输出值，如要增加某一示例被分为“8”的概率，就要降低该示例被分到其他数字（0,1,2,3,4,5,6,7和/或9）的概率。
5.3 Sigmoid和Softmax的其他示例
6、Softmax VS k个二元分类器
如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？
这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）
如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？
在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。
7、ReLu函数和softplus函数
ReLu函数的全称为Rectified Linear Units，函数表达式为y=max(0,x)，softplus函数的数学表达式为y=log(1+ex)，它们的函数表达式如下：
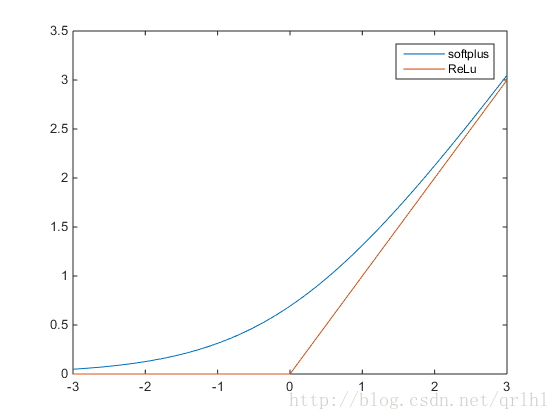
可以看到，softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。
了解更多请参考：http://www.cnblogs.com/neopenx/p/4453161.html
8、总结
如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。
如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。
再学一招：对于那些有一大组标签的情况，要使用softmax激活函数的变体，它被称为分级softmax激活函数，该变体将标签分解为树型结构，并在树的每个节点训练softmax分类器来指导分支进行分类。
参考文献：Deep Learning：A Practitioner's Approach
https://blog.csdn.net/uncle_ll/article/details/82778750
https://blog.csdn.net/u014422406/article/details/52805924
