知识表示之一阶谓词逻辑表示
首先引入知识概念:知识(Knowledge)是人们在改造客观世界的实践中形成的对客观事物(包括自然的和人造的)及其规律的认识,包括对事物的现象、本质、状态、关系、联系和运动等的认识。
知识是把有关的信息关联在一起,形成的关于客观世界某种规律性认识的动态信息结构。
知识=事实+规则+概念:
事实就是指人类对客观世界、客观事物的状态、属性、特征的描述,以及对事物之间关系的描述;
规则是指能表达在前提和结论之间的因果关系的一种形式;
概念主要指事实的含义、规则、语义、说明等。
所谓知识表示(Knowledge Representation),就是把知识用计算机可接受的符号并以某种形式描述出来。
常见的知识表示方式有一阶谓词逻辑,产生式表示,状态空间图表示,与或图表示,语义网络,框架结构表示,还有问题归纳法,面向对象法等。

1. 命题与命题逻辑
命题:是具有真假意义的语句。命题代表人们进行思维时的一种判断,或者是肯定,或者是否定。

命题逻辑:“命题逻辑”是“谓词逻辑”的基础。在现实世界中,有些陈述语句在特定情况下都具有“真”或“假”的含义,在逻辑上称这些语句为“命题”。如:A. 天在下雨 B. 天晴 C. 日照的天气很宜人 D. 我们在辛苦于远程研修中。表达单一意义的命题称为“原子命题”。

命题逻辑就是研究命题和命题之间关系的符号逻辑系统。命题逻辑的联结词:原子命题可通过“联结词”构成“复合命题”,联结词有5种,定义为:
- ﹁表示否定,复合命题“﹁Q”即“﹁Q”
- ∧表示合取,复合命题“P∧Q”表示“P与Q”
- ∨表示析取,复合命题“P∨Q”表示“P或Q”
- →表示条件(蕴含),复合命题“P→Q”表示“如果P,那么Q”
- ↔表示双条件(等价),复合命题“P↔Q”即表示“P当且仅当Q”
2. 谓词与谓词逻辑


谓词逻辑是命题逻辑的扩充和发展,它将一个原子命题分解成个体和谓词两个组成部分。在谓词公式 P(x) 中,P 称为谓词,x 称为个体变元,若 x 是一元的,称为一元谓词, P(x,y) 称为二元谓词。
在谓词中,个体可以为常量,变量,函数。若谓词中的个体都为常量,变量或函数,则称它为一阶谓词,如果个体本身是谓词,称为二阶谓词,依次类推。
谓词公式也有原子谓词公式、复合谓词公式等概念,利用命题逻辑的联结词将原子逻辑化式组合为复合谓词公式。
谓词逻辑的量词(Quantifiers):量词表示了个体与个体域之间的包含关系,谓词逻辑中有两个量词:全称量词(Universal Quantifiers),表示了该量词作用的辖域为个体域中“所有的个体 x ”或“每一个个体都”要遵从所约定的谓词关系;存在量词(Existential Quantifier),表示了该量词要求“存在于个体域中的某些个体 x ”或“某个个体 x ”要服从所约定的谓词关系。

3. 谓词公式
由下述规则得到的谓词公式称为合式公式:
- 单个谓词和单个谓词的否定称为原子谓词公式,原子谓词公式是合式公式
- 若A是合式公式,则﹁A也是合式公式
- 若A、B都是合式公式,则A∨B、A∧B、A→B也都是合式公式
- 若A是合式公式, x 是任一个体变元,则(x )A和(x )A也都是合式公式
在合式公式中,连词的优先级别依序为:﹁,∧,∨,→

谓词公式的解释:在命题逻辑中,对命题公式中各个命题的一次真值指派称为命题公式的一个解释。一个谓词公式的解释可能有很多个。对于每一个解释,谓词公式都可求出一个真值( T 或 F )。
用谓词公式表示知识的步骤如下:
- 定义用谓词及个体,确定每个谓词及个体的确切含义;
- 根据所要表达的事物或概念,为每个谓词中的变元赋以特定的值;
- 根据所要表达的知识的语义,用适当的连接符号将各个谓词连接起来,形成谓词公式。
原子谓词公式:若t1,t2,…,tn是项,P是谓词,则称P(t1,t2,…,tn)为原子谓词公式。
谓词公式的性质:


相关规则:
- 原子公式是谓词公式。
- 若A是谓词公式,其否定也是。
- 若A,B是谓词公式,其进行的合取与析取运算也是。
- 若A是谓词公式,x是项,对x的约束量词表达式产生的也是谓词公式。
量词的辖域
量词的约束范围,即指位于量词后面的单个谓词或者用括弧括起来的合式公式。例:

约束变元:受到量词约束的变元,即辖域内与量词中同名的变元称为约束变元
自由变元:不受约束的变元称为自由变元
例·:

变元的换名:谓词公式中的变元可以换名。要保持变量的论域不变。
约束条件:(存在量词约束的变量换名也一样)
- 对约束变元,必须把同名的约束变元都统一换成另外一个相同的名字,且不能与辖域内的自由变元同名。

- 对辖域内的自由变元,不能改成与约束变元相同的名字。
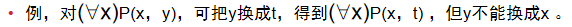
谓词公式真值表:取出公式中所有单个谓词,按所有可能的取值组合,再按连接词和量词的定义给出合适公式的真值。例: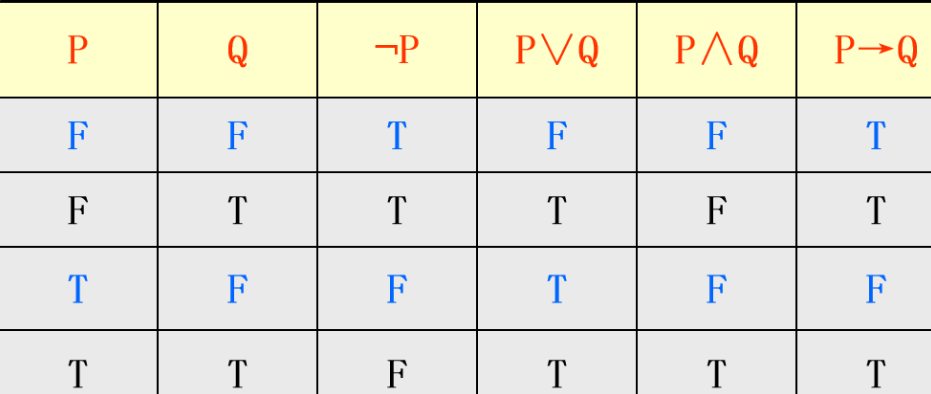
等价公式:



这里的量词转换中,对任意往往使用析取来代替描述,对存在则使用合取来描述。

谓词逻辑表示步骤:先根据要表示的知识定义谓词,再用连词、量词把这些谓词连接起来。
11.一阶谓词逻辑表示法的特点
(1)优点
1.严密性:可以保证其演绎推理结果的正确性,可以比较精确的表达知识
2.自然性:它的表达方式和人类自然语言非常接近
3.通用性:拥有通用的逻辑演算方法和推理规则
4.知识易于表达:对逻辑的某些外延进行扩展后,可以把大部分精确性的知识表达成一阶谓词逻辑的形式
5.易于实现:用它表示的知识易于模块化,便于知识的增删及修改,便于在计算机上实现
(2)缺点
1.效率低:推理过程太冗长,降低了系统效率。谓词表示越细,表达越清楚,推理越慢,效率越低
2.灵活性差:不便于表达和加入启发性知识和元知识,不便于表达不确定性的指示。
3.组合爆炸:在其推理过程中,随着事实数目的增大及盲目地使用推理规则,有可能产生组合爆炸。
参考:https//blog.csdn.net/diamonjoy_zone/article/details/66476374


 浙公网安备 33010602011771号
浙公网安备 33010602011771号