支持向量机（SVM）必备概念(凸集和凸函数，凸优化问题，软间隔，核函数，拉格朗日乘子法，对偶问题，slater条件、KKT条件）

SVM目前被认为是最好的现成的分类器，SVM整个原理的推导过程也很是复杂啊，其中涉及到很多概念，如：凸集和凸函数，凸优化问题，软间隔，核函数，拉格朗日乘子法，对偶问题，slater条件、KKT条件还有复杂的SMO算法！

相信有很多研究过SVM的小伙伴们为了弄懂它们也是查阅了各种资料，着实费了不少功夫！本文便针对SVM涉及到的这些复杂概念进行总结，希望为大家更好地理解SVM奠定基础（图片来自网络）。

一、凸集和凸函数

在讲解凸优化问题之前我们先来了解一下凸集和凸函数的概念

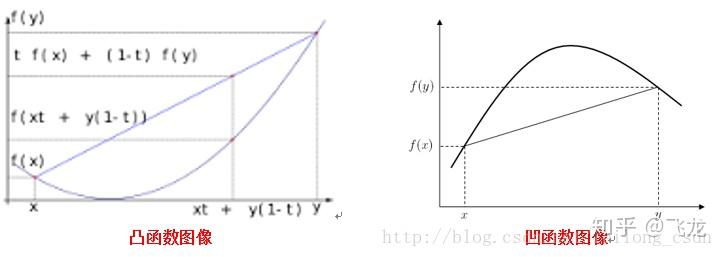
凸集：在点集拓扑学与欧几里得空间中，凸集是一个点集，其中每两点之间的直线上的点都落在该点集中。千言万语不如一张图来的明白，请看下图：

凸函数：一个定义在向量空间的凸子集C(区间)上的实值函数f，如果在其定义域C上的任意两点x，y以及t∈[0,1]有：

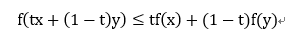
则该函数为凸函数！凸函数另一个判别方式是：如果一个凸函数是一个二阶可微函数，则它的二阶导数是非负的。上图：

下面引自维基百科：

注意：中国大陆数学界某些机构关于函数凹凸性定义和国外的定义是相反的。Convex Function在某些中国大陆的数学书中指凹函数。Concave Function指凸函数。但在中国大陆涉及经济学的很多书中，凹凸性的提法和其他国家的提法是一致的，也就是和数学教材是反的。举个例子，同济大学高等数学教材对函数的凹凸性定义与本条目相反，本条目的凹凸性是指其上方图是凹集或凸集，而同济大学高等数学教材则是指其下方图是凹集或凸集，两者定义正好相反。另外，也有些教材会把凸定义为上凸，凹定义为下凸。碰到的时候应该以教材中的那些定义为准。

在机器学习领域大多数是采用上文中所描述的凸函数和凹函数的定义，下文中凸函数的定义也采用上文描述的那种！

二、凸优化问题

凸优化：凸优化是指一种比较特殊的优化，是指求取最小值的目标函数为凸函数的一类优化问题。其中，目标函数为凸函数且定义域为凸集的优化问题称为无约束凸优化问题。而目标函数和不等式约束函数均为凸函数，等式约束函数为仿射函数，并且定义域为凸集的优化问题为约束优化问题。

上面是来自百度百科定义，下面我们对其总结，将其公式化！

凸优化性质：
1、目的是求取目标函数的最小值；
2、目标函数和不等式约束函数都是凸函数，定义域是凸集；
3、若存在等式约束函数，则等式约束函数为仿射函数；
4、对于凸优化问题具有良好的性质，局部最优解便是全局最优解。

一个凸优化问题用公式描述为：

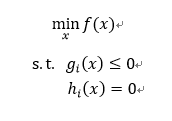
所以其目标函数f(x)以及不等式约束条件g(x)便是凸函数，而等式约束条件h(x)是仿射函数。

大家可能要问：何为仿射函数！！！

仿射函数：即是deg(h(x))=1的函数，常数项为0的仿射函数称为线性函数。

其中符号 deg() 表示多项式h(x)的次数<将函数看成多项式而已>

三.软间隔

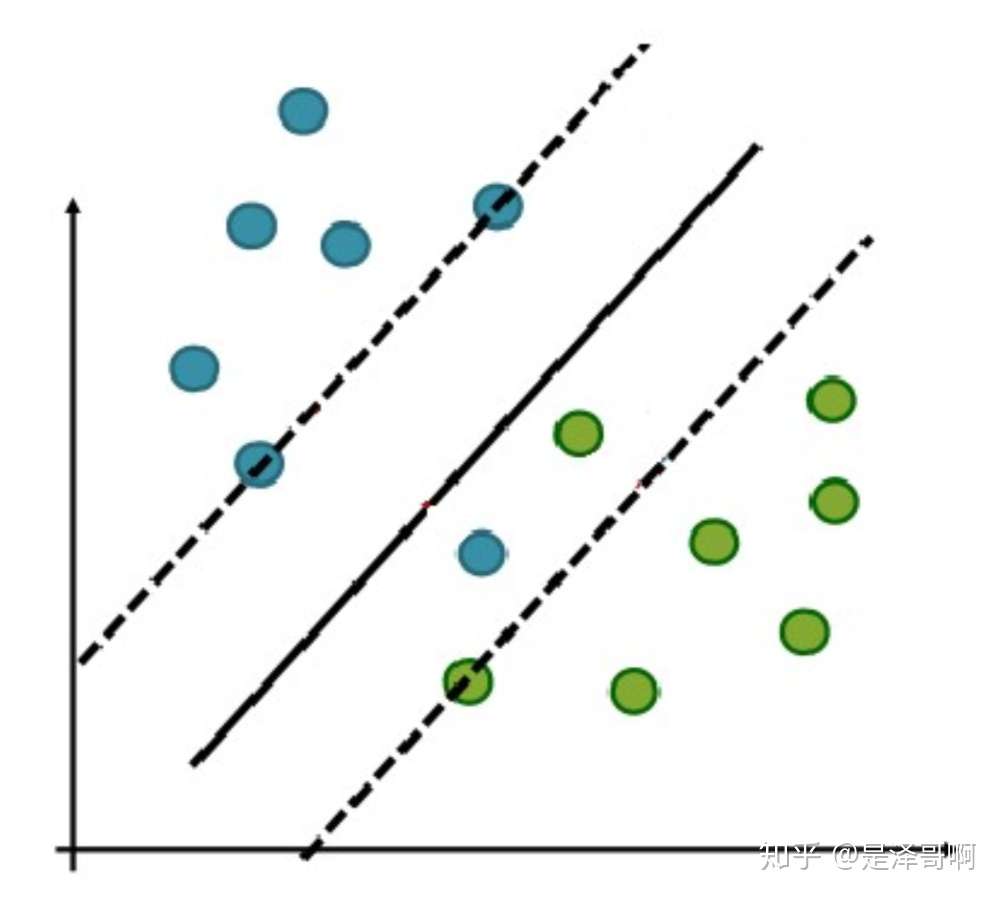
在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，我们应该怎么办？比如下面这个：

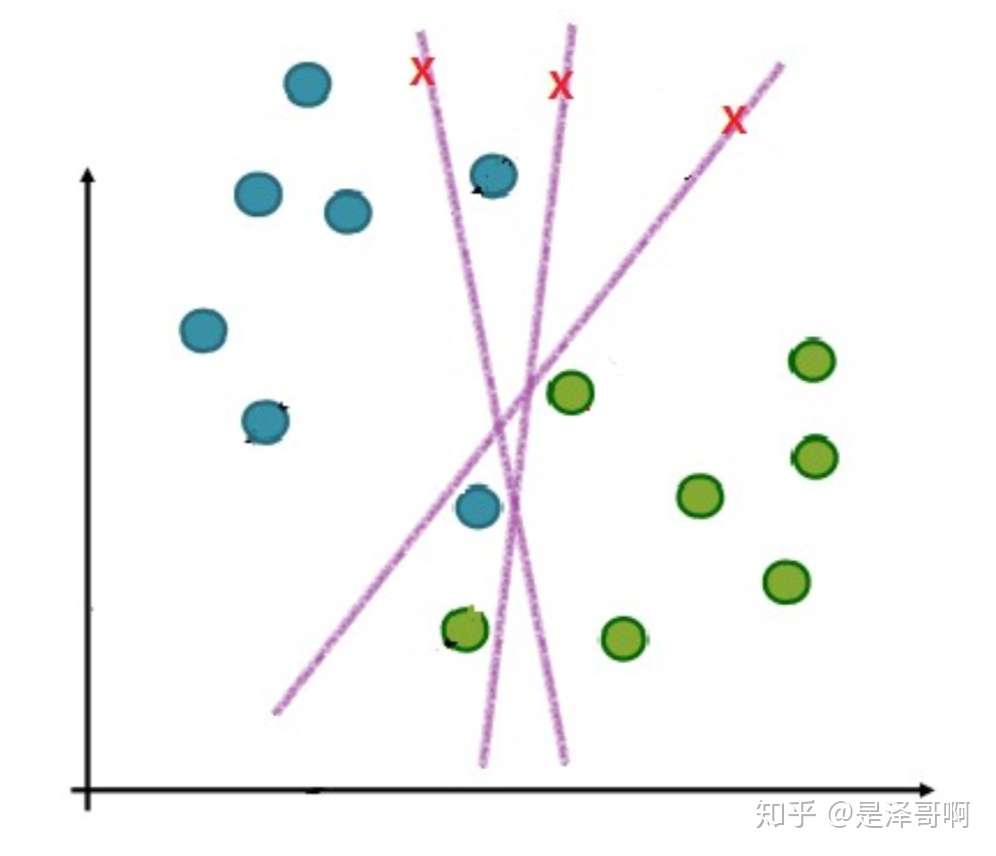
于是我们就有了软间隔，相比于硬间隔的苛刻条件，我们允许个别样本点出现在间隔带里面，比如：

图片来自网络

我们允许部分样本点不满足约束条件：

$1-y_i(w^Tx_i + b) \leq 0 \\$

为了度量这个间隔软到何种程度，我们为每个样本引入一个松弛变量 $\xi_{i}$ ，令 $\xi_{i} \geq 0$ ，且 $1 - y_i(w^Tx_i + b)-\xi_i \leq 0$ 。对应如下图所示：

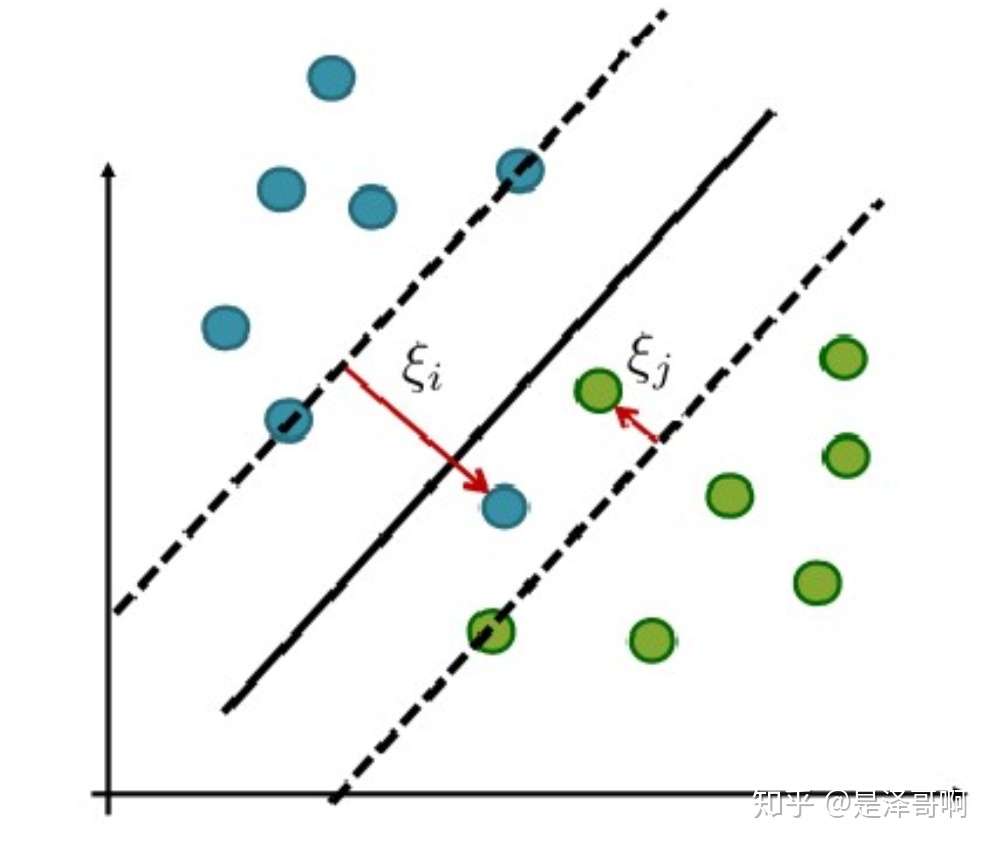
优化目标及求解

增加软间隔后我们的优化目标变成了：

$\min\limits_{w} \frac{1}{2} ||w||^2 + C\sum_{i=1}^{m}\xi_i \\ s.t.\quad g_i(w,b) = 1 - y_i(w^Tx_i+b) - \xi_i\leq 0, \quad \xi_i \geq 0, \quad i=1,2,...,n \\$

其中 C 是一个大于 0 的常数，可以理解为错误样本的惩罚程度，若 C 为无穷大， $\xi_{i}$ 必然无穷小，如此一来线性 SVM 就又变成了线性可分 SVM；当 C 为有限值的时候，才会允许部分样本不遵循约束条件。

接下来我们将针对新的优化目标求解最优化问题：

步骤 1：

构造拉格朗日函数：

$\min\limits_{w,b,\xi}\max\limits_{\lambda, \mu} L(w,b,\xi,\lambda,\mu)= \frac{1}{2}{||w||}^2 + C\sum_{i=1}^{m}\xi_i+ \sum\limits_{i = 1}^n \lambda_i [1-\xi_i-y_i(w^Tx_i+b)] - \sum_{i=1}^{n}\mu_i\xi_i \\ s.t. \quad \lambda_i \geq 0 \quad \mu_i \geq 0 \\$

其中 $\lambda_{i}$ 和 $\mu_{i}$ 是拉格朗日乘子，w、b 和 $\xi_{i}$ 是主问题参数。

根据强对偶性，将对偶问题转换为：

$\max\limits_{\lambda, \mu}\min\limits_{w,b,\xi} L(w,b,\xi,\lambda,\mu) \\$

步骤 2：

分别对主问题参数w、b 和 $\xi_{i}$ 求偏导数，并令偏导数为 0，得出如下关系：

$w = \sum_{i=1}^{m}\lambda_i y_i x_i \\ 0 = \sum_{i=1}^{m}\lambda_i y_i \\ C = \lambda_i + \mu_i \\$

将这些关系带入拉格朗日函数中，得到：

$\min\limits_{w,b,\xi}L(w,b,\xi,\lambda,\mu) = \sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) \\$

最小化结果只有 $\lambda$ 而没有 $\mu$ ，所以现在只需要最大化 $\lambda$ 就好：

$\max\limits_{\lambda} [\sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j)] \\ s.t. \quad \sum_{i=1}^{n}\lambda_iy_i = 0, \quad \lambda_i \geq 0, \quad C-\lambda_i-\mu_i=0 \\$

我们可以看到这个和硬间隔的一样，只是多了个约束条件。

然后我们利用 SMO 算法求解得到拉格朗日乘子 $\lambda^{*}$ 。

步骤 3 ：

$w = \sum_{i=1}^m \lambda_i y_i x_i \\ b = \frac{1}{|S|}\sum_{s \in S} (y_s -wx_s) \\$

然后我们通过上面两个式子求出 w 和 b，最终求得超平面 $w^Tx+b=0$ ，

这边要注意一个问题，在间隔内的那部分样本点是不是支持向量？

我们可以由求参数 w 的那个式子可看出，只要 $\lambda_{i} > 0$ 的点都能够影响我们的超平面，因此都是支持向量。

4. 核函数

4.1 线性不可分

我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。

但我们可能会碰到的一种情况是样本点不是线性可分的，比如：

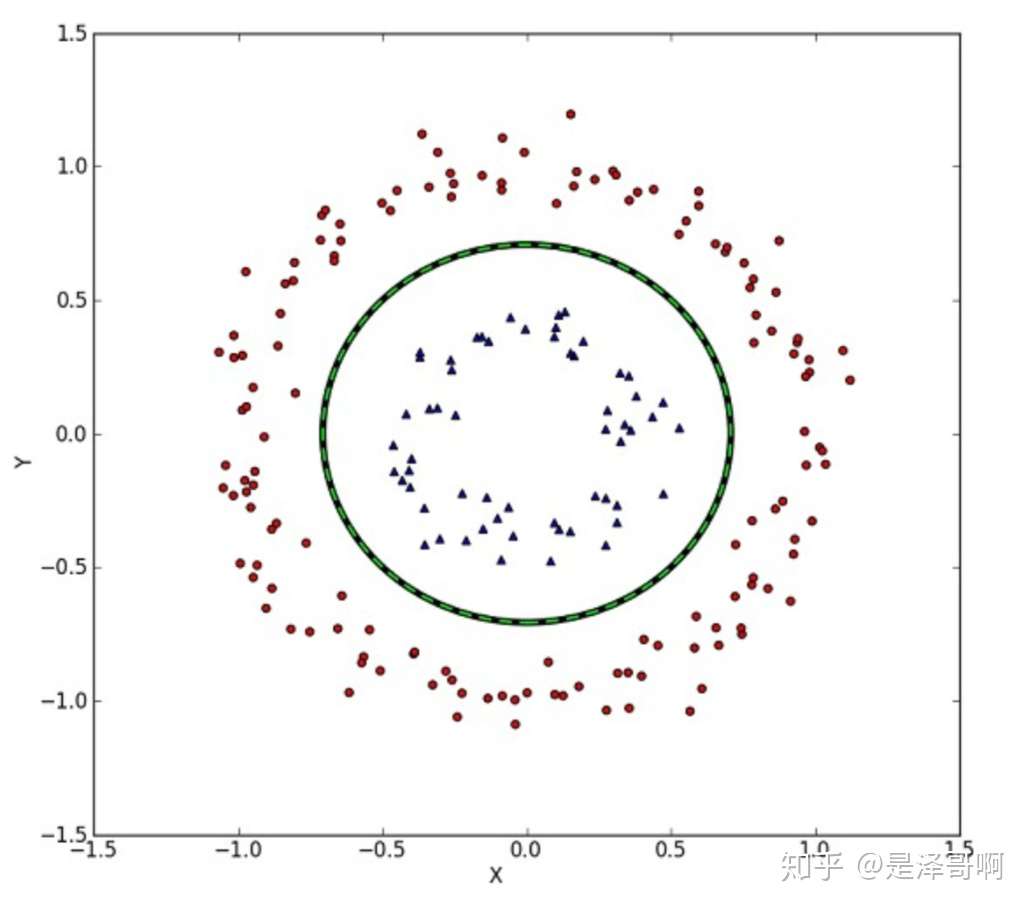
这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，比如：

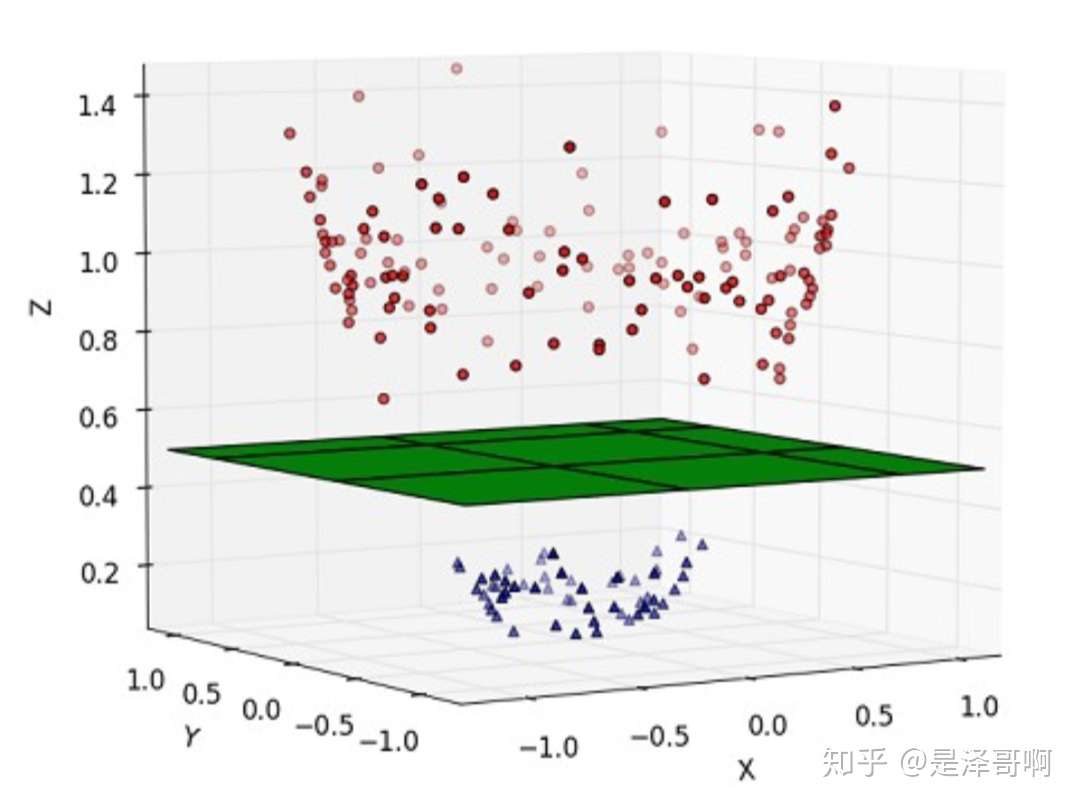
对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

我们用 x 表示原来的样本点，用 $\phi(x)$ 表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为： $f(x)=w \phi(x)+b$ 。

对于非线性 SVM 的对偶问题就变成了：

$\min\limits_{\lambda} [\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (\phi(x_i) \cdot \phi(x_j))-\sum_{j=1}^{n}\lambda_i] \\ s.t. \quad \sum_{i=1}^{n}\lambda_iy_i = 0, \quad \lambda_i \geq 0, \quad C-\lambda_i-\mu_i=0 \\$

可以看到与线性 SVM 唯一的不同就是：之前的 $(x_i \cdot x_j)$ 变成了 $(\phi(x_i) \cdot \phi(x_j))$ 。

4.2 核函数的作用

我们不禁有个疑问：只是做个内积运算，为什么要有核函数的呢？

这是因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。

但如果我们有这样的一核函数 $k(x,y) = (\phi(x),\phi(y))$ ， $x_i$ 与 $x_j$ 在特征空间的内积等于它们在原始样本空间中通过函数 $k( x, y)$ 计算的结果，我们就不需要计算高维甚至无穷维空间的内积了。

举个例子：假设我们有一个多项式核函数：

$k(x,y)=(x \cdot y + 1)^2 \\$

带进样本点的后：

$k(x,y) = (\sum_{i=1}^n(x_i \cdot y_i) + 1)^2 \\$

而它的展开项是：

$\sum_{i=1}^nx_i^2y_i^2+\sum_{i=2}^n\sum_{j=1}^{i-1}(\sqrt2x_ix_j)(\sqrt2y_iy_j)+\sum_{i=1}{n}(\sqrt2x_i)(\sqrt2y_i)+1 \\$

如果没有核函数，我们则需要把向量映射成：

$x^{'} = (x_1^2,...,x_n^2,...\sqrt2x_1,...,\sqrt2x_n,1) \\$

然后在进行内积计算，才能与多项式核函数达到相同的效果。

可见核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

4.3 常见核函数

我们常用核函数有：

线性核函数

$k(x_i,x_j) = x_i^Tx_j \\$

多项式核函数

$k(x_i,x_j) = (x_i^Tx_j)^d\\$

高斯核函数

$k(x_i,x_j) = exp(-\frac{||x_i-x_j||}{2\delta^2}) \\$

这三个常用的核函数中只有高斯核函数是需要调参的。

五、拉格朗日乘子法

拉格朗日乘子法的作用：求函数f(x1,x2…)在g（x1,x2…）=0的约束条件下的极值。

拉格朗日乘子法的操作过程：
（1）定义新函数：

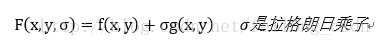
（2）利用偏导方式列出以下方程：

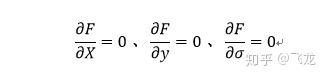
（3）求解出x，y，σ的值带入F（x,y,σ）便是目标函数的极值。

六、对偶问题,slater条件,KKT条件

这里我们来谈一谈SVM中必须需要明白的对偶问题，要说对偶问题，则需要从凸优化问题开始说起。假设我们现在来求解上面的那个凸优化问题的最优解：

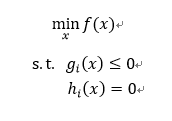
观察上面的最优化问题，便是在一定的约束条件下求解函数的极值，我们上面已经说过拉格朗日乘子法啦，所以这里便用到了。

使用拉格朗日乘子法针对上面的最优化问题有：

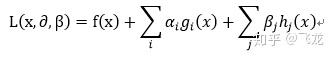
需要明确：其中α≥0、β任意，均为拉格朗日乘子，i=1,2,…,p且j=1,2,…,q

如果按照我们上面谈到的拉格朗日乘子法的思路，则应该让L(x,α,β)对x以及参数α和β进行求导，然后得出结果带入原始便可求出我们需要的最优解。

但需要注意两点：
（1）这里参数α和β总共p+q个，如果全部求偏导工作量太大，不现实；
（2）并且大家有没有想过，这个问题可能根本就没有最优解这种情况存在。

针对上面情况，我们便引出了换一种思路，那就是利用对偶问题，也就是将原问题转化成其对偶问题进行求解。

下面和大家先说一下对偶问题的基本思想，然后我们再继续从上面的问题出发，推导其对偶问题，进行求解。

对偶问题的性质：无论原命题的形式如何，对偶问题都是一个凸优化问题，还记得凸优化问题的好处吧，那就是局部最优解就是全局最优解，并且容易求解，所以我们将问题转化为其对偶问题就简化了问题的求解思路。

上面我们利用拉格朗日乘子法得到了如下式子：

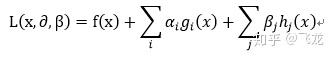
现在我们自定义一个函数如下：

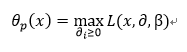
此处有问题：求解SVM时为什么要最大化而不是最小化拉格朗日函数？

见https://zhuanlan.zhihu.com/p/140910622

分析上面的自定义函数有：

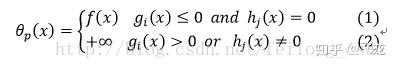
对上面的式子进行分析：

（1）式说明，当目标函数的约束条件都满足时，则自定义的函数便是上面需要求解的目标函数f(x)，（2）则是只要目标函数的约束条件只有一个不满足，则自定义的函数便等于无穷大！

所以我们便可以认为自定义的函数θ(x) 是对原理优化问题中的约束条件进行了吸收，是原来的约束优化问题变为无约束优化问题（相对于原来变量x 无约束了），即我们可以将最初的优化问题写成：

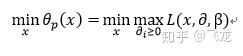
上式便是我们需要优化的原问题（上面还不是对偶问题，只是原问题的转化）

原问题的对偶问题便是：

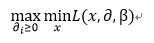
下面我们假设假命题为P，对偶问题为Q！当然对偶问题已经不等价于原问题了，但是二者是存在一定联系的，下面我们来讲解二者的联系，以及如何通过求解对偶问题来得到原问题的最优解！

这里我们令：

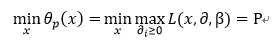
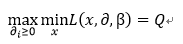
所以有： P<=Q
解释：大家想一下，函数L中最大值中最小的一个总比最小值中最大的那一个要大，也就是对偶问题提供了原问题最优值的一个下界。

但是大家想，我们是想通过对偶问题求解原问题的最优解，所以只有当二者相等时即P=Q，才可能将原问题转化成对偶问题进行求解。当然，当满足一定条件的情况下，便有P=Q。而这个条件便是 slater条件和KKT条件。

slater条件：

slater条件官方正规定义：存在x，使得不等式约束g(x)<=0严格成立。
slater条件性质： slater条件是原问题P可以等价于对偶问题Q的一个充分条件，该条件确保了鞍点的存在。

KKT条件：

大家已经知道slater条件已经确保了鞍点的存在，但是鞍点不一定就是最优解啊，所以KKT条件的作用便体现出来了。
KKT条件便是确保鞍点便是原函数最优解的充分条件，当然对于我们前面举得那个例子，当原问题是凸优化问题时，则KKT条件便是鞍点便是最优解的充要条件。

注意：

KKT条件描述为一下三个条件：

1、

2、

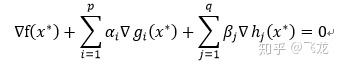
3、

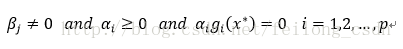
解释：第一个约束条件表明：最优点x必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解, 这一点自然是毋庸置疑的；
第二个约束条件表明：在最优点x, ∇f必须是∇gi和∇hj的线性組合;
第三个约束条件表明：拉格朗日乘子不等式的一些限制，对于不等式的拉格朗日乘子限制条件有方向性, 所以每一个α都必须大于或等于零, 而等式限制条件没有方向性，只是β不等于0。

这样对于slater条件和KKT条件都十分清楚了吧，并且也知道了他们的作用！这样我们最初的求解凸优化问题便转化为求解其对偶问题。当前我们的优化目标便是：

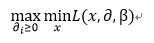
因此我们先让L函数对x求导然后最小化，得出一个优化函数，然后在让这个优化函数对α，β求导，求出参数α，β！这样再待会原问题中，便可得到最优解，而下面我们要将的 SMO算法（序列最小化算法），正是用于求解参数α，β的！

关于SMO算法数学推导十分复杂，我将在后继博客中对于详细阐述其数学推导过程！

问题 SVM 为什么要从原始问题变为对偶问题来求解：

这个问题困扰了我许久，下面是我搜集整理到的答案供大家参考交流部

对偶问题将原始问题中的约束转为了对偶问题中的等式约束
方便核函数的引入
改变了问题的复杂度。由求特征向量w转化为求比例系数a，在原始问题下，求解的复杂度与样本的维度有关，即w的维度。在对偶问题下，只与样本数量有关。

参考：https://blog.csdn.net/feilong_csdn/article/details/62427148

posted @ 2020-10-15 12:39 Chen洋阅读(2451) 评论(0) 编辑收藏举报

刷新页面返回顶部

Chen洋