FixMatch+DST论文阅读笔记(待复现)
FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence
论文标题:FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence
论文作者:Kihyuk Sohn, David Berthelot, Chun-Liang Li, Zizhao Zhang, Nicholas Carlini, Ekin D. Cubuk, Alex Kurakin, Han Zhang, Colin Raffel
论文来源:NeurIPS 2020
代码来源:Code
介绍
半监督学习有效的利用没有标注的数据,从而提高模型的精度。这篇论文,我们将有效的结合两种常见的半监督学习方法:一致性正规化技术和伪标签技术。我们的算法叫做FixMatch,首先把没有标签的图片进行轻微的数据增强,用模型对怎强后的图片进行预测,从而生成为标签。对于每张没有标签的图片,当模型的预测得分高于一定的阈值时,伪标签才起作用。模型预测伪标签的同时,将同样的图片进行强烈的数据增强送入网络,计算损失。虽然方法看起来简单,但是FixMatch在从多的半监督学习方法中达到了最好的效果。仅用了250张标注数据,在CIFAR-10数据集上达到了94.93%的准确率;仅用了40张标注数据,在CIFAR-10数据集上达到了88.61%的准确率(每个类别只取了4张标注数据);因为作者做了很多消融实验,说明不同因素对半监督学习效果的影响,最终FixMatch这种半监督学习方法获得成功。
FixMatch
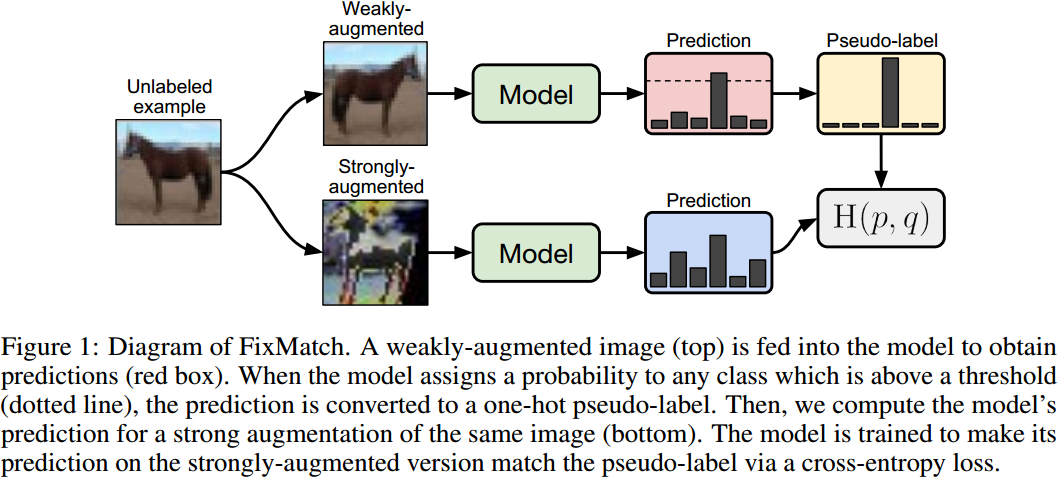
整个过程如上图所示:首先,图片进行轻微的数据增强,然后输入网络进行预测,生成one-hot编码的伪标签。然后,把同样的图片进行强烈的数据增强,得到预测特征。如果轻微数据增强的预测得分大于一定的阈值,那么生成的伪标签就和强烈数据增强的特征计算交叉熵损失。
具体步骤
符号定义
![]()
![]()
定义\(p_m(y|x)\)为模型在输入\(x\)下的类别分布预测。
定义两个概率分布\(p\)和\(q\)之间的交叉熵损失为\(H(p,q)\),用来衡量两个概率分布的差异。
定义强弱两种增强的操作为\(\mathcal{A}(·)\)和\(\alpha(·)\)。
方法
FixMatch的损失函数有两部分组成:有标签的图片用有监督的损失\(\mathcal{l}_s\),没有标签的图片用无监督的损失\(\mathcal{l}_u\), 两个损失都是标准的交叉熵损失:
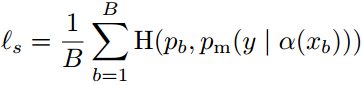
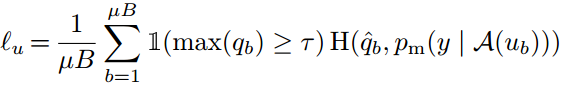
对于没有标签图片的处理:首先得到伪标签,如果伪标签的得分大于一定的阈值(τ,论文中的阈值取0.95),那么,就用该伪标签和强烈数据增强获得的特征计算交叉熵损失。
最后,FixMatch的最终损失为:
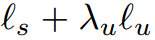
Debiased Self-Training for Semi-Supervised Learning
论文标题:Debiased Self-Training for Semi-Supervised Learning
论文作者:Baixu Chen, Junguang Jiang, Ximei Wang, Pengfei Wan, Jianmin Wang, Mingsheng Long
论文来源:NIPS 2022 Oral
代码来源:Code
引入
尽管自训练在半监督学习的基准数据集上取得了很好的性能,但我们发现,目前最先进的自训练算法(FixMatch)仍然存在两个主要问题:
训练不稳定:
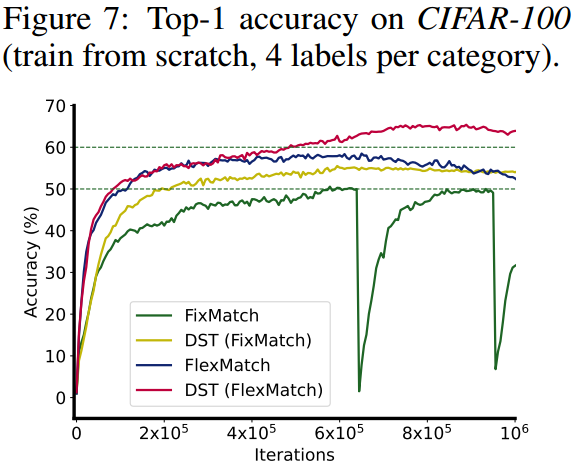
该图展示了使用典型的自训练方法FixMatch训练过程中,模型准确率出现了明显的震荡。
马太效应:
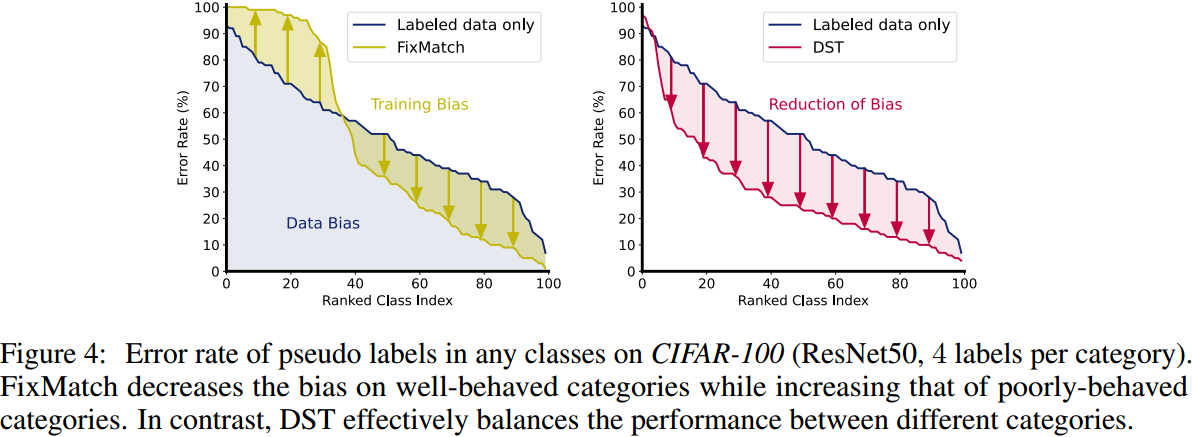
该图展示了使用FixMatch算法训练后,准确率较高的类别会取得更高的准确率,而那些学习的不佳的类别的准确率可能会继续下降甚至接近0。
以上两个问题是由伪标签函数与目标标签函数之间的偏差引起的。使用有偏的、不可靠的伪标签训练模型有可能会导致错误累积,并最终造成模型性能的波动。而对于那些表现不佳的类别,自训练偏差更严重,并且会随着自训练的进行而进一步恶化,最终导致马太效应。
为了解决上述不足,我们系统地分析了半监督学习中的自训练偏差问题。基于分析,我们提出了DST,一种减轻自训练偏差并提高训练稳定性和跨类性能平衡的新方法。
问题分析
首先,我们对自训练中的偏差来源进行分析。自训练的偏差是指学习到的决策超平面与真实决策超平面之间的偏差。它可以近似地通过每个类别的准确度来衡量,因为决策超平面的偏差越大,相关类别的准确度就越低。
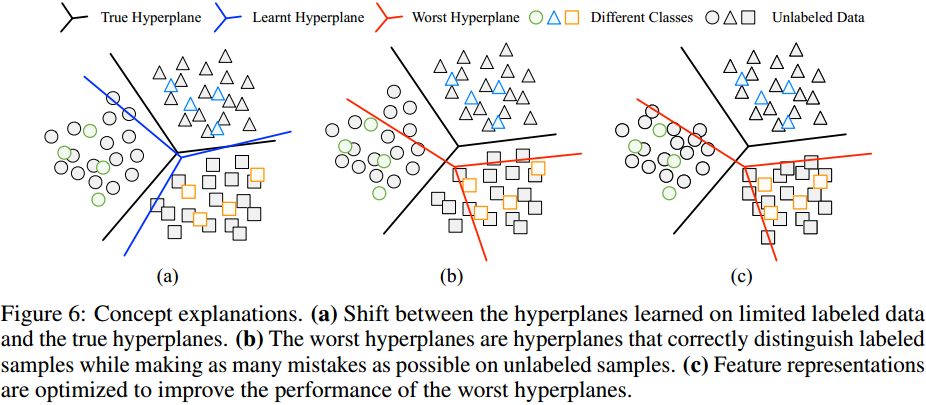
通过分析不同训练条件下各类别的准确率,我们有以下发现:
标注数据的采样将在很大程度上影响自训练偏差。当标注数据的采样不同时,同一类别的准确率可能很高也可能很低。原因是不同数据点与真实决策超平面之间的距离并不相同,一些数据点更近,而另一些则相对远离。当标注数据较少时,每个类别采样到的数据与真实决策超平面之间的距离可能会有很大差异,因此学习到的决策超平面会偏向某些类别:
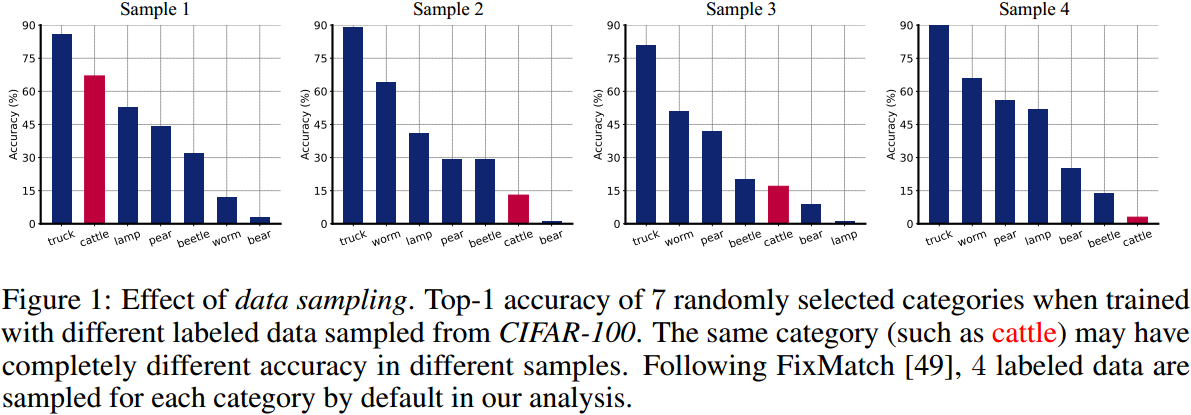
模型的预训练方法也会影响自训练偏差。即使预训练数据集和下游标记数据集都是相同的,不同的预训练方法会导致不同的类别偏向。一个可能的原因是不同的预训练模型学习的表示关注数据的不同方面。因此,相同的数据也可能在不同预训练模型的特征表示上与决策超平面有不同的距离:
使用伪标签进行训练反而增大了自训练偏差。在使用伪标签(比如FixMatch))进行训练后,不同类别的性能差距显著扩大,而某些类别的准确率从 60% 提高到 80%,某些类别的准确率从 15% 下降到 0%。这是因为对于那些网络学习的较好的类别,伪标签几乎是准确的,因此将它们用于训练可以进一步减少偏差。但是对于很多网络学习较差的类别,伪标签是不可靠的,常见的伪标签训练机制会进一步增加偏差,并且难以在后续训练中被纠正。

基于以上观察,我们将自训练引起的偏差分为两类:
- 数据偏差(Data Bias):半监督学习任务中固有的偏差,例如数据的采样和预训练特征表示导致的偏差。
- 训练偏差(Training Bias):由自训练策略导致的偏差扩大。
接下来我们将介绍如何减少自训练中的训练偏差和数据偏差。
方法设计
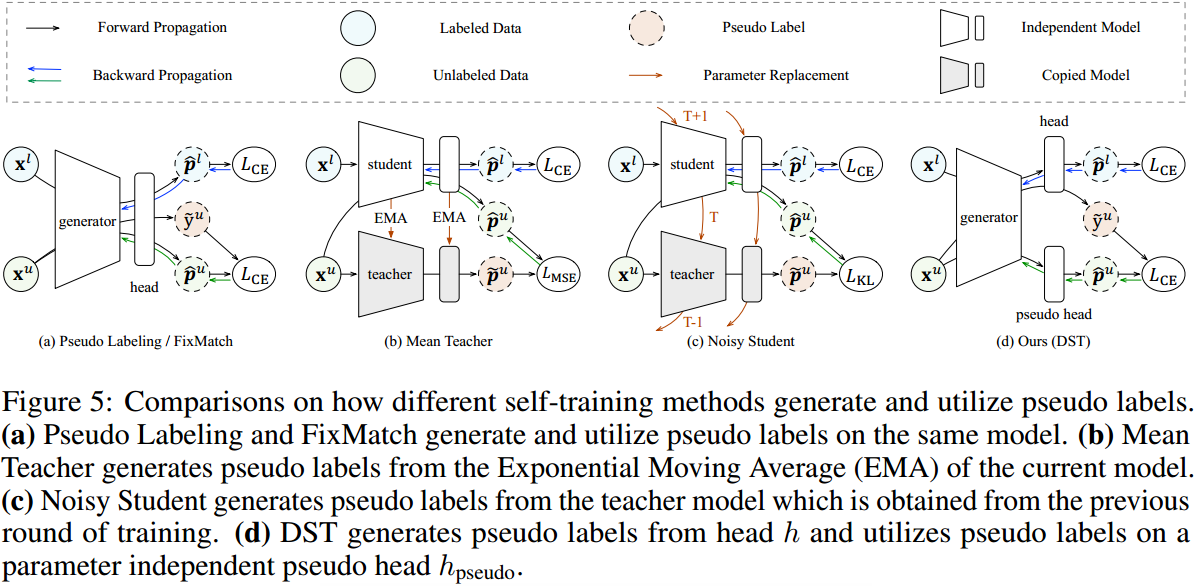
减少训练偏差—解耦伪标签生成与利用
FixMatch的训练偏差来源于使用自身生成的伪标签进行训练的机制。为了减少这种偏差,一些方法转而通过更好的教师模型生成伪标签,例如平均老师算法(Mean Teacher)使用当前模型的滑动平均作为教师模型。然而,这种方法中生成伪标签的教师模型和利用伪标签的学生模型之间仍然存在联系,学生模型的决策超平面仍然可能会被错误的伪标签函数所影响 。因此,在自训练过程中仍然存在训练偏差。
为了消除使用伪标签时的训练偏差,我们只使用有标注数据 \(\mathcal{L}\) 中准确的标签,而不再使用无标注数据 \(\mathcal{U}\) 中的任何伪标签(它们很可能是不可靠的)来优化分类器头 \(h\) 。为了防止深度模型过度拟合少数有标注样本,我们仍然使用伪标签进行训练,但只是为了学习更好的特征表示。
如上图的(d)所示,引入了一个代理分类器头\(h_{pseudo}\),它直接和特征提取器\(\psi\)相连,并且只使用来自\(\mathcal{U}\)的伪标签进行优化。完整的优化目标是
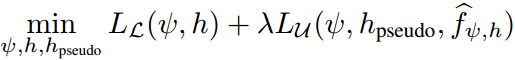
其中伪标签由分类器头\(h\)生成,但通过一个完全独立的代理分类器头\(h_{pseudo}\)被利用。这种解耦机制可以有效地消除在分类器头\(h\)上进行自训练所导致的偏差累积。代理分类器头\(h_{pseudo}\)只负责在训练期间向特征提取器\(\psi\)进行梯度的反向传播,在推理过程中其会被丢弃,因此不会引入额外的计算负担。
减少数据偏差—估计最坏训练偏差
前一小节提出了一种消除训练偏差的解决方案,但伪标签函数\(\hat f\)中仍然存在数据偏差。

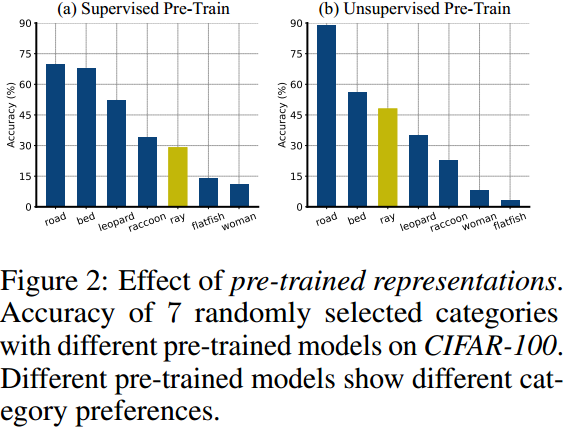
如图(a)所示,由于数据偏差的存在,每个类别的有标注样本到表示空间中的决策超平面的距离不同,这导致学习到的超平面和真正的决策超平面之间存在偏差,特别是有标注样本的数量非常少时。因此,伪标签函数\(\hat f\)很可能会在靠近这些有偏决策超平面的未标记数据点上生成不正确的伪标签。而我们现在的目标是优化特征表示以减少数据偏差,最终提高伪标签的质量。
由于我们没有\(\mathcal{U}\)上的标注,我们不能直接测量从而减少数据偏差。然而,训练偏差与数据偏差有一些相关性。在上一节中,分类器头\(h\)仅使用准确的有标注数据进行优化,这是因为使用不正确的伪标签进行优化会将学习的超平面推向偏差更大的方向并导致训练偏差。因此,训练偏差可以认为是在伪标签使用不当时数据偏差的累积,这是依赖于训练算法的。而所有训练方法中能达到的最差训练偏差可以更好地衡量数据偏差的程度。通过减少最差训练偏差,我们可以间接地降低数据偏差。具体来说,最差的训练偏差对应于通过伪标记学习到的最差的分类器头\(h^{’}\),\(h^{’}\)对所有有标注的样本\(\mathcal{L}\)预测正确,同时在无标注的数据\(\mathcal{U}\)上尽可能地犯错:
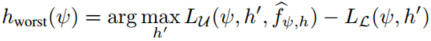
其中\(h^{’}\)在无标注数据上的错误是通过其与当前伪标签函数\(\hat f\)的差异来估计的。该公式刻画了未来在当前特征提取器\(\psi\)上使用伪标签训练时可能学习到的分类器头\(h\)的最坏情况。图(c)可视化最差超平面,其尽可能地与目前所学习到的超平面远离,同时保证所有有标注样本都被正确分类。
注意到\(h_worst\)依赖于\(\psi\)生成的特征表示,因此我们可以优化特征提取器\(\psi\)以减少最坏情况偏差:
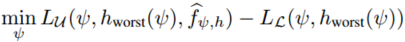
该公式鼓励特征提取器产生使得最差的超平面也能正确区分无标注样本的特征,从而在特征表示层面减少数据偏差。
最终目标函数
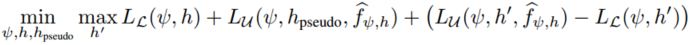
实验