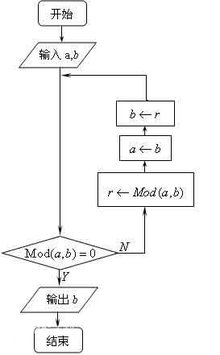
求最大公约数伪代码

算法说明与链接

欧几里德算法又称辗转相除法，用于计算两个整数a，b的最大公约数。其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b

假设d是a,b的一个公约数，则有

d|a, d|b，而r = a - kb，因此d|r

因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则

d | b ， d |r ，但是a = kb +r

因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证。

链接：https://baike.so.com/doc/5875750-6088617.html

 伪代码

Write"Enter the num1"

Read num2

Write"Enter the num2"

Read num1

Set quotient to num1%num2

WHILE(quotient is not zero )

Set num1 to num2

Set num2 to quotient

Set quotient to num1%num2

Set answer to num2

Write answer

选择几组数据，手动走一下伪代码，测试你写的伪代码是否正确，提交测试过程截图