Java基础语法(8)-数组中的常见排序算法
title: Java基础语法(8)-数组中的常见排序算法
blog: CSDN
data: Java学习路线及视频
1.基本概念
- 排序: 是计算机程序设计中的一项重要操作,其功能是指一个数据元素集合或序列重新排列成一个按数据元素某个数据项值有序的序列.
- 排序码(关键码): 排序依据的数据项.
- 稳定排序: 排序前与排序后相同关键码元素间的位置关系,保持一致的排序方法.
- 不稳定排序: 排序前与排序后相同关键码元素间的相对位置发生改变的排序方法.
- 内排序: 指待排序列完全存放在内存中所进行的排序.内排序大致可分为五类
- 插入排序
- 交换排序
- 选择排序
- 归并排序
- 分配排序
- 外排序: 指排序过程中还需访问外存储器的排序.
2.选择排序
操作方法
第一趟:从n个记录中找出关键码最小的记录和第一个记录交换;
第二趟:从第二个记录开始的n-1个记录中再选出关键码最小的记录与第二个记录交换
以此类推......
第i趟,则从第i个记录开始的n-i+1个记录中选出关键码最小的记录与第i个记录交换,直到整个序列按关键码有序。
/**
* 直接选择排序
* @author BenCoper
* 2020-04-01
*/
public class SelectSort {
public static void selectSort(int[] data) {
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 0; i < arrayLength - 1; i++) {
for (int j = i + 1; j < arrayLength; j++) {
if (data[i] - data[j] > 0) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
System.out.println(java.util.Arrays.toString(data));
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
selectSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
选择排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n²) | O(n²) | O(1) |
3.插入排序
操作方法
一组无序序列{A1,A2,........An} 先取出A1,
然后从A2与A1比较,比较完之后序列状况是{A1,A2}{A3..........An},
其中{A1,A2}有序, 然后取出A3 ,放到{A1,A2}有序序列合适位置,
导致{A1,A2,A3}{A4........An}。
重复这个过程,直到取出An{A1,A2........An-1}有序序列中。
/**
* 直接插入排序
* @author BenCoper
* 2020-04-01
*/
public class InsertSort {
public static void insertSort(int[] data) {
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 1; i < arrayLength; i++) {
int temp = data[i];
if (data[i] - data[i - 1] < 0) {
int j = i - 1;
for (; j >= 0 && data[j] - temp > 0; j--) {
data[j + 1] = data[j];
}
data[j + 1] = temp;
}
System.out.println(java.util.Arrays.toString(data));
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
insertSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n) | O(n²) | O(1) |
4.堆排序

操作方法
构建初始堆,将待排序列构成一个大顶堆(或者小顶堆),升序大顶堆,降序小顶堆;
将堆顶元素与堆尾元素交换,并断开(从待排序列中移除)堆尾元素。
重新构建堆。
重复2~3,直到待排序列中只剩下一个元素(堆顶元素)。
/**
* 堆排序
* @author BenCoper
* 2020-04-01
*/
public class HeapSort {
public static void heapSort(int[] data) {
System.out.println("开始排序");
int arrayLength = data.length;
// 循环建堆
for (int i = 0; i < arrayLength - 1; i++) {
// 建堆
buildMaxdHeap(data, arrayLength - 1 - i);
// 交换堆顶和最后一个元素
swap(data, 0, arrayLength - 1 - i);
System.out.println(java.util.Arrays.toString(data));
}
}
// 对data数组从0到lastIndex建大顶堆
private static void buildMaxdHeap(int[] data, int lastIndex) {
// 从lastIndex处节点(最后一个节点)的父节点开始
for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
// k保存当前正在判断的节点
int k = i;
// 如果当前k节点的子节点存在
while (k * 2 + 1 <= lastIndex) {
// k节点的左子节点的索引
int biggerIndex = 2 * k + 1;
// 如果biggerIndex小于lastIndex,即biggerIndex +1
// 代表k节点的右子节点存在
if (biggerIndex < lastIndex) {
// 如果右子节点的值较大
if (data[biggerIndex] - data[biggerIndex + 1] < 0) {
// biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
// 如果k节点的值小于其较大子节点的值
if (data[k] - data[biggerIndex] < 0) {
// 交换它们
swap(data, k, biggerIndex);
// 将biggerIndex赋给k,开始while循环的下一次循环
// 重新保证k节点的值大于其左、右节点的值
k = biggerIndex;
} else {
break;
}
}
}
}
// 交换data数组中i、j两个索引处的元素
private static void swap(int[] data, int i, int j) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
heapSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(nlogn) | O(1) |
5.归并排序
操作方法
归并排序是先将数组进行拆分,拆分到剩余一个关键字,这是一个从大到小的过程。
然后再进行治理,治理的过程也就是进行合并的过程,合并时会保证左右两边的数组内部各自有序。
然后将两个有序的数组合并到一个数组中,且合并后的数组有序。总结就是:递归拆分,回溯合并,合并时左右两个数组内部有序。
/**
* 堆排序
* @author BenCoper
* 2020-04-01
*/
public class MergeSort {
public static void mergeSort(int[] data) {
// 归并排序
sort(data, 0, data.length - 1);
}
// 将索引从left到right范围的数组元素进行归并排序
private static void sort(int[] data, int left, int right) {
if(left < right){
//找出中间索引
int center = (left + right)/2;
sort(data,left,center);
sort(data,center+1,right);
//合并
merge(data,left,center,right);
}
}
// 将两个数组进行归并,归并前两个数组已经有序,归并后依然有序
private static void merge(int[] data, int left, int center, int right) {
int[] tempArr = new int[data.length];
int mid = center + 1;
int third = left;
int temp = left;
while (left <= center && mid <= right) {
if (data[left] - data[mid] <= 0) {
tempArr[third++] = data[left++];
} else {
tempArr[third++] = data[mid++];
}
}
while (mid <= right) {
tempArr[third++] = data[mid++];
}
while (left <= center) {
tempArr[third++] = data[left++];
}
while (temp <= right) {
data[temp] = tempArr[temp++];
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
mergeSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(nlogn) | O(1) |
6.基数排序

操作方法
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。
然后,从最低位开始,依次进行一次排序。
这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
/**
* 基数排序
* @author BenCoper
* 2020-04-01
*/
public class MultiKeyRadixSort {
public static void radixSort(int[] data, int radix, int d) {
System.out.println("开始排序:");
int arrayLength = data.length;
int[] temp = new int[arrayLength];
int[] buckets = new int[radix];
for (int i = 0, rate = 1; i < d; i++) {
// 重置count数组,开始统计第二个关键字
Arrays.fill(buckets, 0);
// 当data数组的元素复制到temp数组中进行缓存
System.arraycopy(data, 0, temp, 0, arrayLength);
for (int j = 0; j < arrayLength; j++) {
int subKey = (temp[j] / rate) % radix;
buckets[subKey]++;
}
for (int j = 1; j < radix; j++) {
buckets[j] = buckets[j] + buckets[j - 1];
}
for (int m = arrayLength - 1; m >= 0; m--) {
int subKey = (temp[m] / rate) % radix;
data[--buckets[subKey]] = temp[m];
}
System.out.println("对" + rate + "位上子关键字排序:"
+ java.util.Arrays.toString(data));
rate *= radix;
}
}
public static void main(String[] args) {
int[] data = { 1100, 192, 221, 12, 13 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
radixSort(data, 10, 4);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n) | O(n²) | O(1) |
7.冒泡排序
操作方法
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
/**
* 冒泡排序
* @author BenCoper
* 2020-04-01
*/
public static void bubbleSort1(int[] data) {
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 0; i < arrayLength - 1; i++) {
boolean flag = false;
for (int j = 0; j < arrayLength - 1 - i; j++) {
if (data[j] > data[j + 1]) {
int temp = data[j + 1];
data[j + 1] = data[j];
data[j] = temp;
flag = true;
}
}
System.out.println(java.util.Arrays.toString(data));
if (!flag)
break;
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
bubbleSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n) | O(n²) | O(1) |
8.快速排序
操作方法
通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,
则分别对这两部分继续进行排序,直到整个序列有序。
/**
* 快速排序
* @author BenCoper
* 2020-04-01
*/
public class QuickSort {
private static void swap(int[] data, int i, int j) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
private static void subSort(int[] data, int start, int end) {
if (start < end) {
int base = data[start];
int low = start;
int high = end + 1;
while (true) {
while (low < end && data[++low] - base <= 0)
;
while (high > start && data[--high] - base >= 0)
;
if (low < high) {
swap(data, low, high);
} else {
break;
}
}
swap(data, start, high);
subSort(data, start, high - 1);//递归调用
subSort(data, high + 1, end);
}
}
public static void quickSort(int[] data){
subSort(data,0,data.length-1);
}
public static void main(String[] args) {
int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
quickSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(n²) | O(1) |
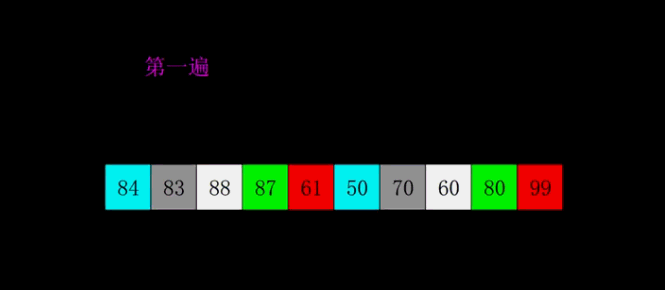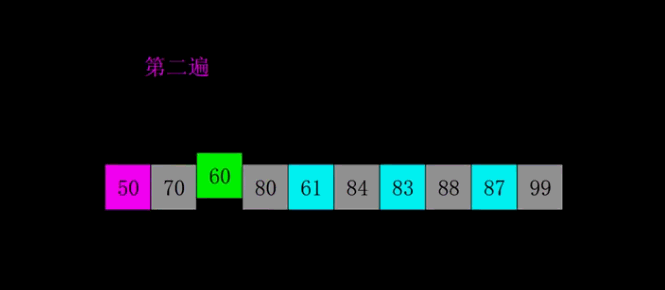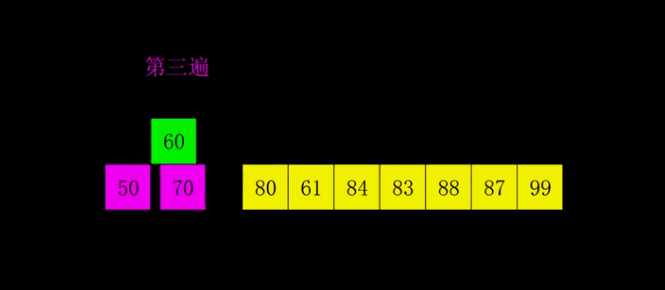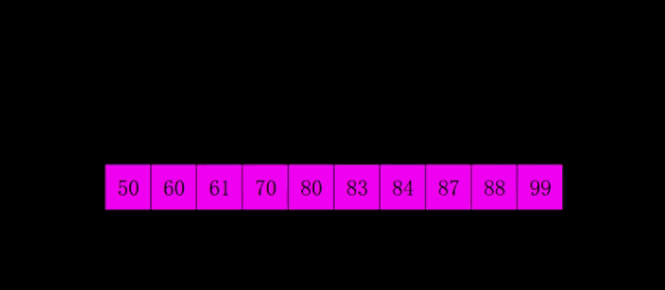
9.希尔排序
操作方法
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
/**
* Shell排序
* @author BenCoper
* 2020-04-01
*/
public class ShellSort {
public static void ShellSort(int[] data) {
System.out.println("开始排序");
int arrayLength = data.length;
int h = 1;
while (h <= arrayLength / 3) {
h = h * 3 + 1;
}
while (h > 0) {
System.out.println("===h的值:" + h + "===");
for (int i = h; i < arrayLength; i++) {
int temp = data[i];
if (data[i] - data[i - h] < 0) {
int j = i - h;
for (; j >= 0 && data[j] - temp > 0; j -= h) {
data[j + h] = data[j];
}
data[j + h] = temp;
}
System.out.println(java.util.Arrays.toString(data));
}
h = (h - 1) / 3;
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
ShellSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
插入排序的时间复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n^(1.3—2)) | O(n) | O(n²) | O(1) |
10.结语

2020-3-31: Java基础语法(6)-注释
2020-3-31: Java基础语法(7)-数组
-
今日好文推荐
-
今日资料推荐
嘴里说的人生就是以后自己的人生
