算法很美 笔记 4.多维数组与矩阵
4.多维数组与矩阵
题1 :顺时针打印二维数组
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100
public int[] spiralOrder(int[][] matrix) {
int[] result =new int[]{};
if(matrix.length==0){
return result;
}
int leftUpRow=0,leftUpCol=0,rightDownRow=matrix.length-1,rightDownCol=matrix[0].length-1;
result=new int[matrix.length*matrix[0].length];
int index=0;
if(matrix==null){
return result;
}
while(leftUpCol<=rightDownCol&&leftUpRow<=rightDownRow){
//打印第一行
int row=leftUpRow,col=leftUpCol;
while(index<result.length&&col<=rightDownCol){//上
result[index++]=matrix[row][col++];
}
//恢复
col=rightDownCol;
row++;
while(index<result.length&&row<=rightDownRow){//右
result[index++]=matrix[row++][col];
}
row=rightDownRow;
col--;
while(index<result.length&&col>=leftUpCol){//下
result[index++]=matrix[row][col--];
}
col=leftUpCol;
row--;
while(index<result.length&&row>leftUpRow){//左
result[index++]=matrix[row--][col];
}
leftUpCol++;
leftUpRow++;
rightDownCol--;
rightDownRow--;
}
return result;
}
逻辑清楚,起名知道意思,写一步测一步
题2 : 0所在的行列清零
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
输入:
[[1,1,1],
[1,0,1],
[1,1,1]]
输出:
[[1,0,1],
[0,0,0],
[1,0,1]]
public static void setZeroes(int[][] matrix) {
if(matrix.length==0){
return;
}
int row=matrix.length;
int col=matrix[0].length;
int[] rowMark=new int[row];
int[] colMark=new int[col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if(matrix[i][j]==0){
rowMark[i]=1;
colMark[j]=1;
}
}
}
for (int i = 0; i <row ; i++) {
if(rowMark[i]==1){
for (int j = 0; j < col; j++) {
matrix[i][j]=0;
}
}
}
for (int i = 0; i <col ; i++) {
if(colMark[i]==1){
for (int j = 0; j < row; j++) {
matrix[j][i]=0;
}
}
}
}
题3:z形打印二位数组
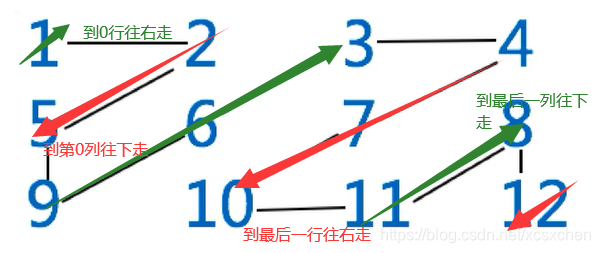
public class Case03_PrintMatrixZig {
public static void main(String[] args) {
int[][] matrix = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
// {13, 14, 15, 16},
};
print(matrix);
}
static void print(int[][] matrix) {
int r = 0, m = matrix.length;
int c = 0, n = matrix[0].length;
boolean l2r = true;//从左到右
while (r < m && c < n) {
//从左下到右上的斜线
if (l2r) {
System.out.print(matrix[r][c] + " ");
//现在在第一行,列未到边界,这是只能向右走
if (r == 0 && c < n - 1) {
l2r = !l2r;//方向切换
c++;
continue;
} else if (r > 0 && c == n - 1) {//现在在最后一列,只能向下走
l2r = !l2r;
r++;
continue;
} else {//继续走上坡
r--;
c++;
}
} else {//反,走下坡
System.out.print(matrix[r][c] + " ");
if (c == 0 && r < m - 1) {//走到第一列,只能往下走
l2r = !l2r;
r++;
continue;
} else if (r == m - 1) {//到最后一行,只能往右走
l2r = !l2r;
c++;
continue;
} else {
r++;
c--;
}
}
}
}
}
题4:边界为1的最大子方阵
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
提示:1 <= grid.length <= 100
1 <= grid[0].length <= 100
public static int largest1BorderedSquare(int[][] grid) {
if(grid.length==0){
return 0;
}
if(grid.length==1){
for (int i = 0; i < grid[0].length; i++) {
if(grid[0][i]==1){
return 1;
}
}
return 0;
}
int row=grid.length,col=grid[0].length;
int N=Math.min(row,col);
for (; N>=1 ; N--) {
for (int i = 0; i <=row-N; i++) {
c1:for (int j = 0; j<=col-N ; j++) {
int r=i,c=j;
while(c<N+j){//up
if(grid[r][c++]==0){
continue c1;
}
}
c--;
while(r<N+i){//right
if(grid[r++][c]==0){
continue c1;
}
}
r--;
while(c>=j){//down
if(grid[r][c--]==0){
continue c1;
}
}
c++;
while(r>=i){//left
if(grid[r--][c]==0){
continue c1;
}
}
r++;
return N*N;
}
}
}
return 0;//{0,0},{0,0}这种情况下执行
}
public static int largest1BorderedSquare(int[][] grid) {
int row = grid.length;
int col = grid[0].length;
// initial
int[][] rowOnes = new int[row][col]; // rowOnes[i][j] = (i,j) 右边连续的 1 数目; 包括 (i,j)
int[][] colOnes = new int[row][col]; // colOnes[i][j] = (i,j) 下边连续的 1 数目; 包括 (i,j)
for (int i = 0; i < row; i++) {//最后一列,右边连续数是1则为1
rowOnes[i][col - 1] = (grid[i][col - 1] == 1 ? 1 : 0);
}
for (int i = 0; i < col; i++) {//最后一行,下边连续是1则是1
colOnes[row - 1][i] = (grid[row - 1][i] == 1 ? 1 : 0);
}
// iteration
for (int i = 0; i <row; i++) {//逐行
for (int j = col - 2; j >= 0; j--) {//从倒数第二列往左
rowOnes[i][j] = (grid[i][j] == 1 ? (rowOnes[i][j + 1] + 1) : 0);//若为1则,右边连续数位右边元素连续数加1
}
}
for (int i = row - 2; i >= 0; i--) {//从倒数第二行往上
for (int j =0; j <col; j++) {//逐列
colOnes[i][j] = (grid[i][j] == 1 ? (colOnes[i + 1][j] + 1) : 0);//若为1则,向下连续数位下边元素连续数加1
}
}
int max = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
for (int m = Math.min(rowOnes[i][j], colOnes[i][j]); m > max; m--) {
if(colOnes[i][j + m - 1] >= m && rowOnes[i + m - 1][j] >= m) {
max = Math.max(max, m);
break;
}
}
}
}
return max * max;
// for(int N=Math.min(row,col);N>=1;N--) {
// for (int i = 0; i <= row-N; i++) {
// for (int j = 0; j <= col-N; j++) {
// if(rowOnes[i][j]>=N&&colOnes[i][j]>=N&&rowOnes[i+N-1][j]>=N&&colOnes[i][j+N-1]>=N){
// return N*N;
// }
// }
// }
// }
// return 0;
}
题5 :子数组最大累加和
-
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
// 暴力法破解 Θ(n²) static void findByForce(int[] arr) { int maxSum = arr[0]; for (int j = 0; j < arr.length; j++) { int sum = arr[j];// 某个元素为子数组的第一个元素 int maxOfJ = sum; for (int i = j + 1; i < arr.length; i++) { sum += arr[i];// 累加后续元素 if (sum > maxOfJ) { maxOfJ = sum; } } if (maxOfJ > maxSum) { maxSum = maxOfJ; } } System.out.println(maxSum); } // 递推法 Θ(n) //如果左边的元素是负的就舍弃 static int findByDp(int[] arr) { // System.out.println("======="+arr.length); if (arr.length == 0) return 0; int sumJ = arr[0]; // 前J个元素的最大贡献 int max = sumJ; int left = 0, right = 0; for (int j = 1; j < arr.length; j++) { if (sumJ >= 0) { // 左子表的最大和为正,继续向后累加 sumJ += arr[j]; } else { sumJ = arr[j]; left = j;//丢弃前部分和的同时,更新left } if (sumJ > max) { max = sumJ; right = j;//更新max的同时更新right } } // System.out.println(max+",left="+left+",right:"+right); return max; }
题6 :子矩阵最大累加和
-
给定一-个矩阵matrix ,其中的值有正、有负、有0 ,返回子矩阵的最大累加和。
-
例如, matrix为:
| -1 | -1 | -1 |
|---|---|---|
| -1 | 2 | 2 |
| -1 | -1 | -1 |
其中最大累加和的子矩阵为:
2 2
所以返回4
//N^3时间复杂度
private static int maxSum(int[][] matrix) {
int beginRow = 0;//以它为起始行
final int M = matrix.length;
final int N = matrix[0].length;
int[] sums = new int[N];//按列求和
int max = 0;//历史最大的子矩阵和
while (beginRow < M) { //起始行
for (int i = beginRow; i < M; i++) {//从起始行到第i行
//按列累加
for (int j = 0; j < N; j++) {
sums[j] += matrix[i][j];
}
// 累加完成
// 求出sums的最大和子数组O(n)
int t = Case05_MaxSubArray.findByDp(sums);
if (t > max)
max = t;
}
//另起一行作为起始行.把sums清零
Arrays.fill(sums, 0);//快速地将sums的每个元素都设定为0
beginRow++;
}
return max;
}
一、矩阵的加法与减法
- 运算规则

简言之,两个矩阵相加减,即它们相同位置的元素相加减!
注意:只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减法运算才有意义,即加减运算是可行的.
- 运算性质(假设运算都是可行的)
满足交换律和结合律
交换律A+B= B+A;
结合律(A+B)+C= A+(B+C).
二、矩阵与数的乘法
-
运算规则
数入乘矩阵λ,就是将数λ乘矩阵A中的每一个元素,记为λA或Aλ.
特别地,称- A称为A=(aij)m xs的负矩阵。 -
运算性质
满足结合律和分配律
结合律: (λu)A=λ(μA); (λ+μ)A =λA+μA.
分配律: λ (A+B)=λA+λB.
三、矩阵与矩阵的乘法
1、运算规则
设A=(aij)mxs,B=(bij) sxn,则A与B的乘积C =AB是这样一一个矩阵 : .
(1)行数与(左矩阵) A相同,列数与(右矩阵) B相同,即C =(cij)mxn.
(2) C的第i行第j列的元素Cq由A的第i行元素与B的第j列元素对应相乘,再取乘积之和.



/**
* 矩阵乘法
* 矩阵1为n*m矩阵,矩阵2为m*p矩阵
* 结果为n*p矩阵
*/
public static long[][] matrixMultiply(long[][] m1, long[][] m2) {
final int n = m1.length;
final int m = m1[0].length;
if (m != m2.length) throw new IllegalArgumentException();
final int p = m2[0].length;
long[][] result = new long[n][p];// 新矩阵的行数为m1的行数,列数为m2的列数
for (int i = 0; i < n; i++) {//m1的每一行
for (int j = 0; j < p; j++) {//m2的每一列
for (int k = 0; k < m; k++) {
result[i][j] += m1[i][k] * m2[k][j];
}
}
}
return result;
}

