Codeforces Round 729 (Div. 2)B. Plus and Multiply（构造、数学）

题面

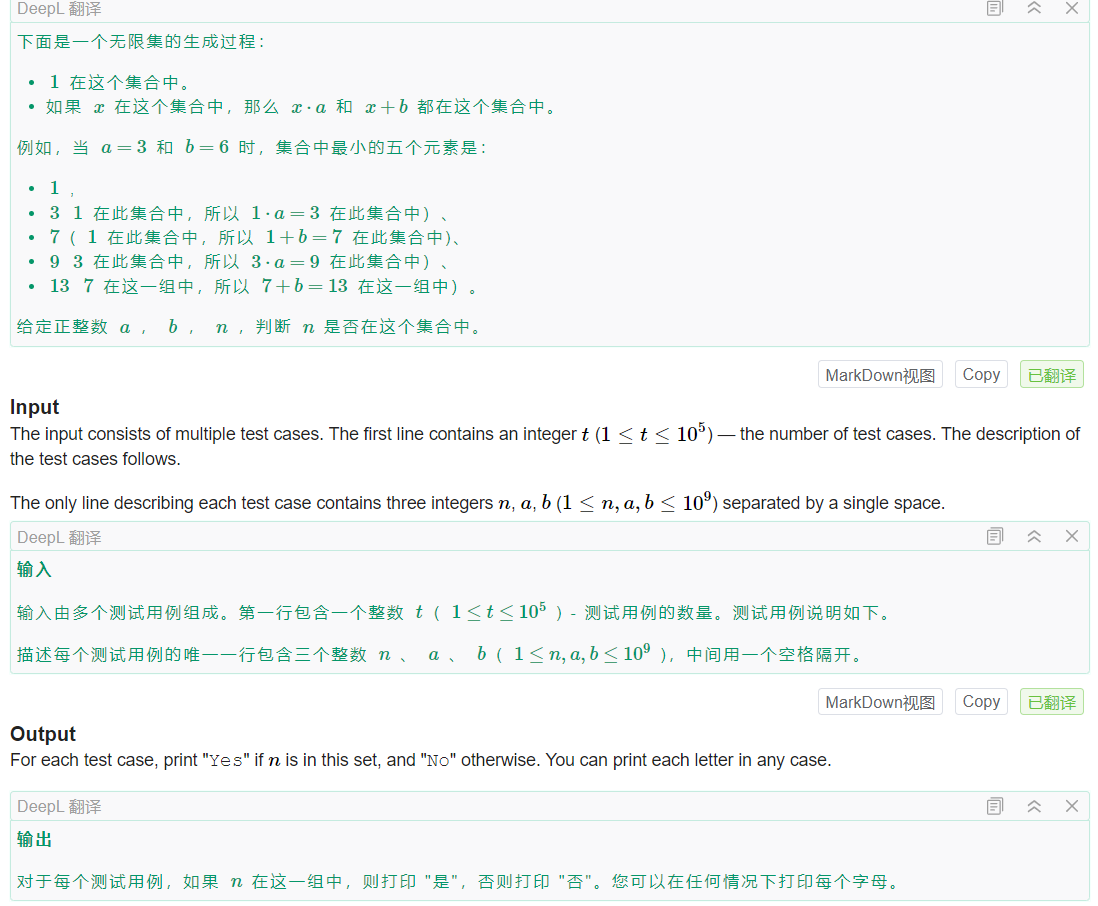
链接

B. Plus and Multiply

题意

给定\(n，a，b\)
可以进行的操作

1. \(*a\)
2. \(+b\)

最开始的数是1
问能否经过上面的两种操作将1变为n

题解

这题的关键是能不能想出来这个集合里面的数的统一的表达形式
所有数都可以表示为
\(a^x+y * b\)
然后只要存在\(x\)和\(y\)，使得\(a^x+y * b=n\)即可
对上式进行等价变换可以得到
\((n-a^x)\equiv0\quad (mod \quad b)\)
还有需要注意的是特判\(a=1\)的情况，因为\(a=1\)时会陷入死循环

代码

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pll pair<long long, long long>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;
const int N=2e5+10;
int a[N];
void solve()
{
	int n,a,b;
	cin>>n>>a>>b;
	if(a==1){
		cout<<((n%b)==(1%b)?"YES":"NO")<<endl;
		return;
	}
	for(int i=1;i<=n;i*=a){
		if((n-i)%b==0){
			cout<<"YES"<<endl;
			return;
		}
	}
	cout<<"NO"<<endl;
}

signed main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
  	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

总结

对数学推式子的能力还是太差，需要多练