树的直径
树的直径
树中两点之间的距离：连接两点的路径上的权值之和
树的直径：树中最远的两个节点之间的距离
树的直径的两种求法，一种是两边bfs or dfs，一种是树形dp
直径的性质
1、直径两端点一定是两个叶子节点
2、距离任意点最远的点一定是直径的一个端点，这个基于贪心求直径方法的正确性可以得出
bfs做法
例题大臣的旅费
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = 2 * N;
int n;
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int v)
{
e[idx] = b, w[idx] = v, ne[idx] = h[a], h[a] = idx ++;
}
LL dist[N];
bool vis[N];
int bfs(int st)
{
queue<int>q;
while(q.size()) q.pop();
memset(vis, 0, sizeof vis);
memset(dist, 0,sizeof dist);
vis[st] = 1;
dist[st] = 0;
q.push(st);
while(q.size())
{
auto t = q.front(); q.pop();
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(!vis[j])
{
dist[j] = dist[t] + w[i];
vis[j] = 1;
q.push(j);
}
}
}
int maxx = -0x3f3f3f3f, pos = 1;
for(int i = 1; i <= n; ++ i)
if(dist[i] > maxx) maxx = dist[i], pos = i;
return pos;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; ++ i)
{
int p, q, d; scanf("%d%d%d", &p, &q, &d);
add(p, q, d);
add(q, p, d);
}
int t1 = bfs(1);
int t2 = bfs(t1);
cout << (1LL) * (dist[t2] + 21) * dist[t2] / 2 << endl;
return 0;
}
树形dp
我们不妨设0号节点为根节点，这样我们就可以将树看为一个有根树，我们用d1，d2两个数组记录从当前节点往下能走的最长链的长度，和次长链的长度，对于每一个点我们取最长和次长链的长度想加，就是树的直径
void dfs_d(int u, int fa)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j != fa)
{
//从下往上算，因为我们要想知道父节点往下走的最远距离，需要
//先知道，子节点向下走的最远距离，然后从下向上传递信息更新
dfs_d(j, u);
int d = d1[j] + 1;
//如果当前子节点+1的距离大于原来u节点存的最大距离的话
//这时我们就需要去更新u节点的最大距离，这里不要忘记更
//更新一下次大距离
if(d > d1[u])
{
d2[u] = d1[u];
d1[u] = d;
p[u] = j;
}
//否则我们退而求其次看当前节点+1的距离能否更新次大距离，
//如果能就将次大距离更新
else if(d > d2[u]) d2[u] = d;
}
}
//每次算完更新一下任意两个端点之间的最大距离
D = max(D, d1[u] + d2[u]);
}
拓展题目旅游规划
预处理
我们先确定一个点为根节点，我们统计一下从当前点开始往下走能走到的最远距离和次远距离，然后我们再dfs一遍预处理出来，一个点向上能走到的最远距离。
1、对于第一个预处理我们可以直接用树的直径的板子求得
2、对于第二个预处理我们做如下考虑
因为我们是求向上走能走的最大距离，所以我们是从上往下去更新的，对于当前节点的每个儿子节点，他们向上走可以转化为父节点怎么走的情况
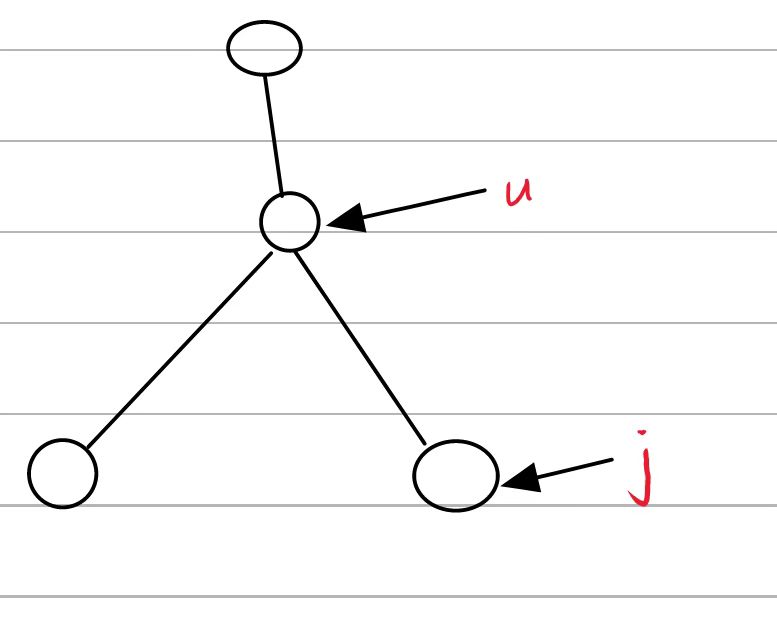
对于u这个节点我们要找到出了e这条边外，其他u节点连接的点向下走的最远距离，或者向上走的最远距离
这里向上走的最远距离我们已经有了，关键是找到除了j这一点外，其他向下走能走到的最远距离，这里可以分两种情况进行讨论，第一种是如果走j就是最大的话，我们就用次小值进行更新，如果不是最大的我们就直接用最大值更新，这里还有一个问题就是我们如何确定j是不是往下走最大的呢？我们在第一个预处理过程中可以用一个数组记录一下当前点往下走那个点是最大的这样的话我们就完成了所有的预处理
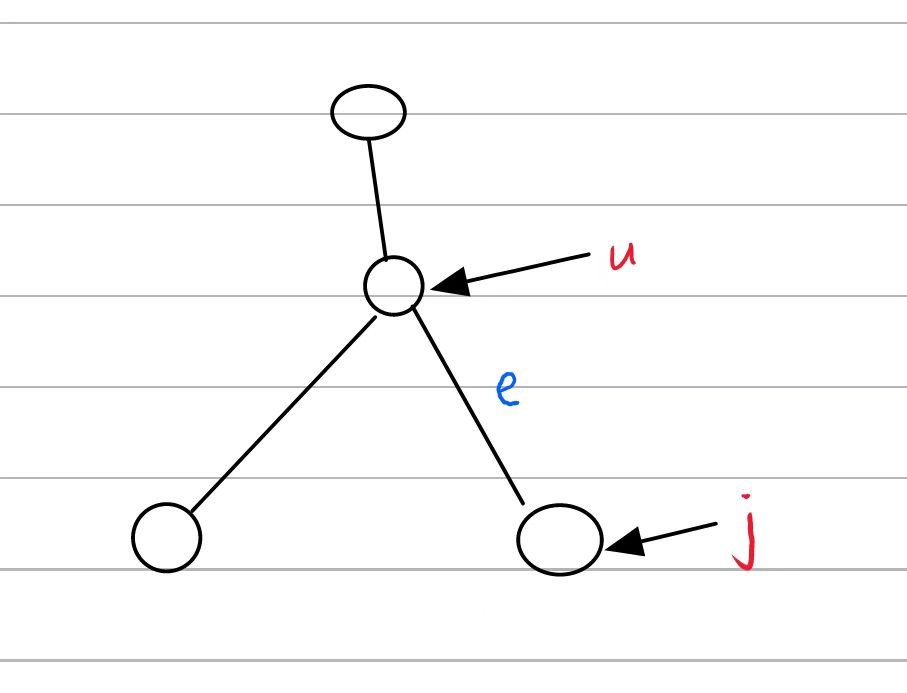
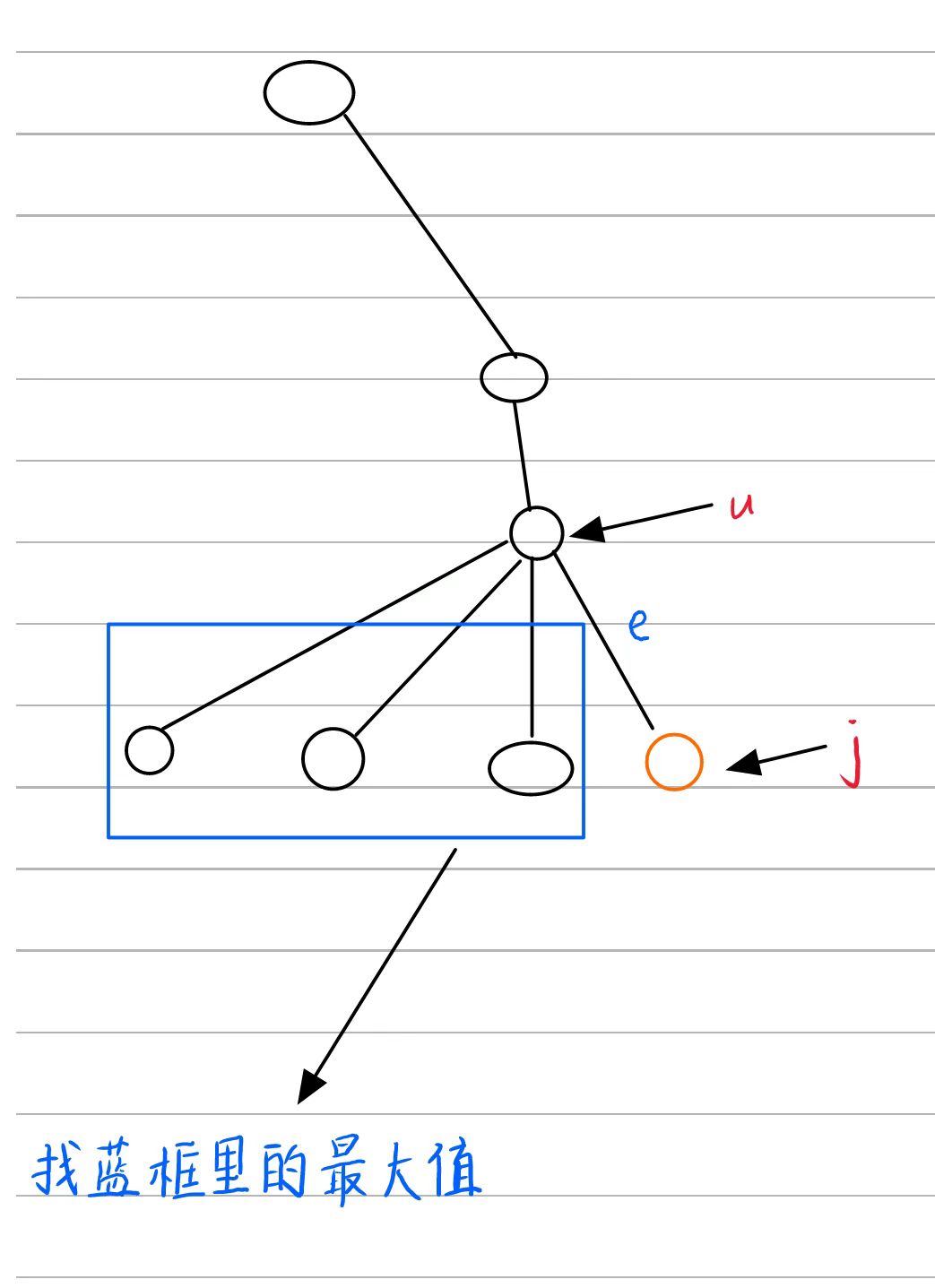
统计答案
我们从前往后枚举每一个点，当一个点向下走的最大距离加向上走的最大距离是直径时说明这个点就在树的直径上
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10, M = N * 2;
int h[N], e[M], ne[M], idx, n;
void add(int a, int b)
{
e[idx] = b; ne[idx] = h[a]; h[a] = idx ++;
}
int d1[N], d2[N], p[N], up[N], D;
//求树的直径，dfs一遍维护，每个点向下走能走的最远距离d1和次远距离d2
void dfs_d(int u, int fa)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j != fa)
{
//从下往上算，因为我们要想知道父节点往下走的最远距离，需要
//先知道，子节点向下走的最远距离，然后从下向上传递信息更新
dfs_d(j, u);
int d = d1[j] + 1;
//如果当前子节点+1的距离大于原来u节点存的最大距离的话
//这时我们就需要去更新u节点的最大距离，这里不要忘记更
//更新一下次大距离
if(d > d1[u])
{
d2[u] = d1[u];
d1[u] = d;
p[u] = j;
}
//否则我们退而求其次看当前节点+1的距离能否更新次大距离，
//如果能就将次大距离更新
else if(d > d2[u]) d2[u] = d;
}
}
//每次算完更新一下任意两个端点之间的最大距离
D = max(D, d1[u] + d2[u]);
}
void dfs_up(int u, int fa)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j != fa)
{
//自上而下更新
//首先，子节点的向上走能走到的最远距离可以先
//向上走一步到u节点，然后我们需要找到除了u-j
//这一条边外其他节点能走的最大值
//这里分为两种情况，一种是，u节点继续向上走，
//两一种就是u节点除去走过的那一条，向下走的最
//大值， 所以这里我们又会有不同的情况，当我们
//走过的条边是我们从u点开始向下走的最大的话我
//就不能用d1[u]去更新，而需要用d2[u]去更新，
//反之我们直接用d1[u]去更新
up[j] = up[u] + 1;
if(j == p[u]) up[j] = max(up[j], d2[u] + 1);
else up[j] = max(up[j], d1[u] + 1);
dfs_up(j , u);
}
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; ++ i)
{
int a, b;scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
dfs_d(0, -1);
dfs_up(0, -1);
for(int i = 0; i < n; ++ i)
{
int a[3] = {d1[i], d2[i], up[i]};
sort(a, a + 3);
if(a[2] + a[1] == D) printf("%d\n", i);
}
return 0;
}
