归并排序求逆序对的数量

逆序对的数量的求法主要运用分治的思想

首先我们先将整个区间分成两段

然后我们将逆序对的情况分成三种情况来求

第一种情况是如下图

首先我们

假设，我们左右区间均已经排好序，现在我们正在归并的过程

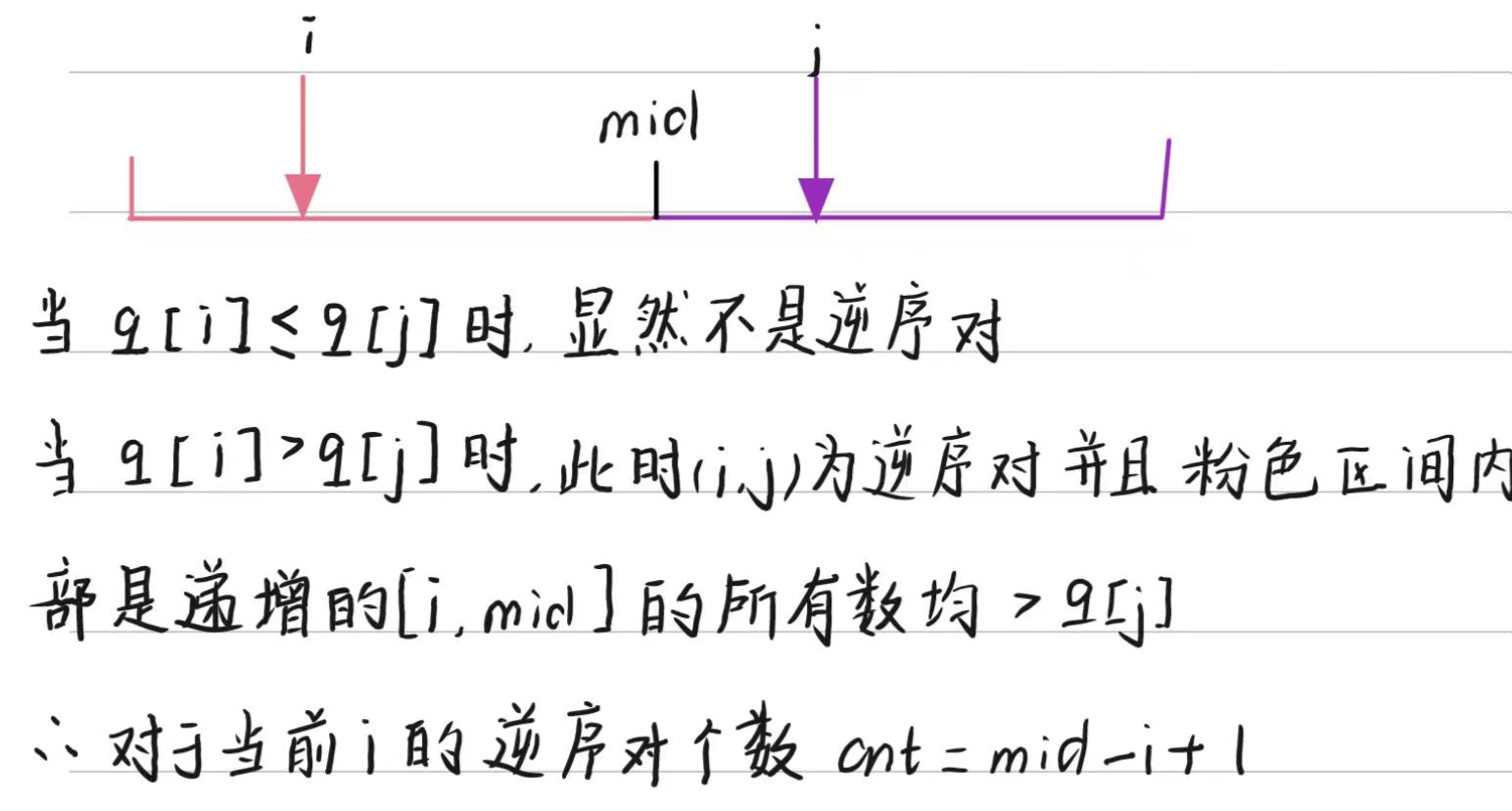
当我们完成这次归并之后，当前这类逆序对的数量我们已经统计完成

我们继续看剩下的两种情况

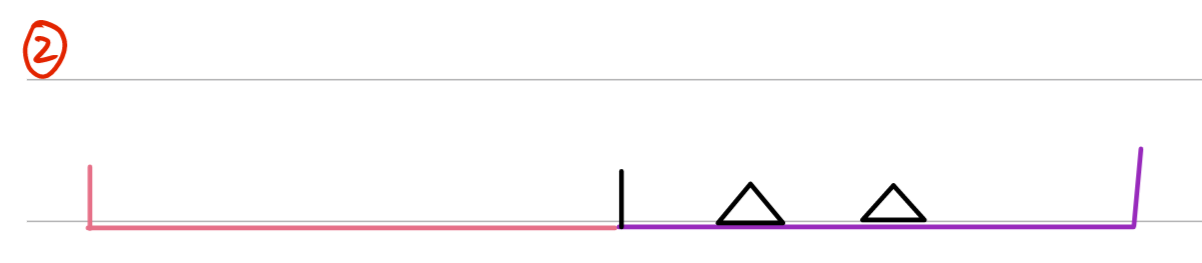
这种情况就是在同侧的逆序对，我们可以发现在求同侧的逆序对这样的问题仍然是求一个区间上的逆序对，这样问题就又变成我们已经解决的第三种情况的逆序对，所有我们只需要递归求解这种情况的逆序对即可】

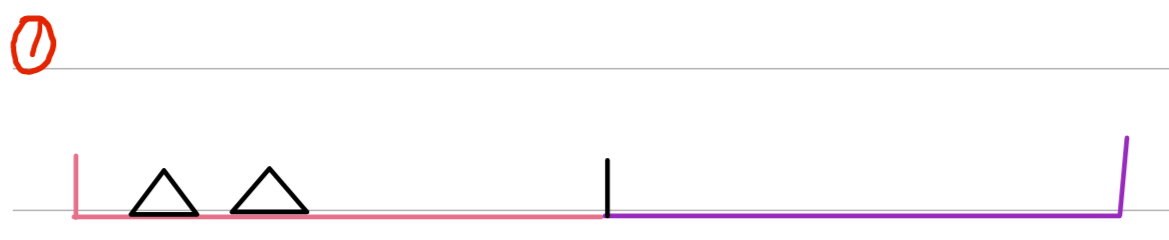
对于第一种情况的逆序对是第二种情况逆序对的对称情况实际上是和第一种情况等价的，我们仍然只需要进行递归求解即可

#include <iostream>

using namespace std;

const int N = 1e6 + 10;
typedef long long LL;

int q[N], tmp[N];
int n;

LL merge_sort(int l, int r)
{
    //当区间中只有一个数时，逆序对的数量为0
    if(l >= r)  return 0;
    int mid = (l + r) >> 1;
    //递归求解两边的逆序对数量
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
    
    //求解第三类逆序对数量
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j])    tmp[k ++] = q[i ++];
        else
        {
            tmp[k ++ ] = q[j ++];
            res += mid - i + 1;
        }
    }
    
    while(i <= mid) tmp[k ++] = q[i ++];
    while(j <= r)   tmp[k ++ ] = q[j ++];
    
    for(int i = l, j = 0; i <= r; ++ i, ++ j)   q[i] = tmp[j];
    return res;
}
int main()
{
    cin >> n;
    for(int i = 0; i < n; ++ i) cin >> q[i];
    cout << merge_sort(0, n - 1) << endl;
    return 0;
}