差分约束问题
差分约束主要求解两个问题
- 不等式的可行解
- 源点需要满足的条件:从源点出发一定可以遍历到所有边
- 求可行解最短路和最长路的做法都可以
- 如何求最大最小值
求可行解的步骤
- 先将每个不等式Xi <= Xj + Ck,转化成从Xj走到Xi的一条边
- 找一个超级源点一定可以遍历到所有的边
- 从源点求一遍单源最短路,如果图中存在负环,则原不等式组一定无解,如果无负环,则dist[i]是原不等式的一组解
不等式的形式为 Xi <= Xj + Ck, Xi 和 Xj均为自变量,Ck为常数,可正可负
我们联想最短路, 当存在从j到i边权为w的边,当 我们跑完最短路时,一定存在dist[i] <= dist[j] + w; 这时我们把前式看作一个不等式,只要图中不存在负环,我们求完最短路之后就可以得到每一个dist的值,就可以求出一组可行解,也就是说,我们可以把不等式看作一条从j走到i的边。
如何求最大值或最小值(最值指的是每个变量的最大值最小值)
结论
- 如果求最小值用最长路
- 如果求最大值用最短路
两个问题
- 如何转化Xi <= c(以最短路为例),其中c是一个常数,这类的不等式
- 方法:建立一个超级源点,0,Xi <= X0 +c,(X0 = 0),建立一条从0到i长度为c的边
以求最大值为例 求所有从Xi出发的不等式链Xi <= Xj + C1 <= Xk + C1 + C2 <= 0 + C1 +C2 + … +,所计算出的上界,最终Xi的最大值是所有上界的最小值, 每一条链式不等式都是一条从0到i的路径。最长路是同理的
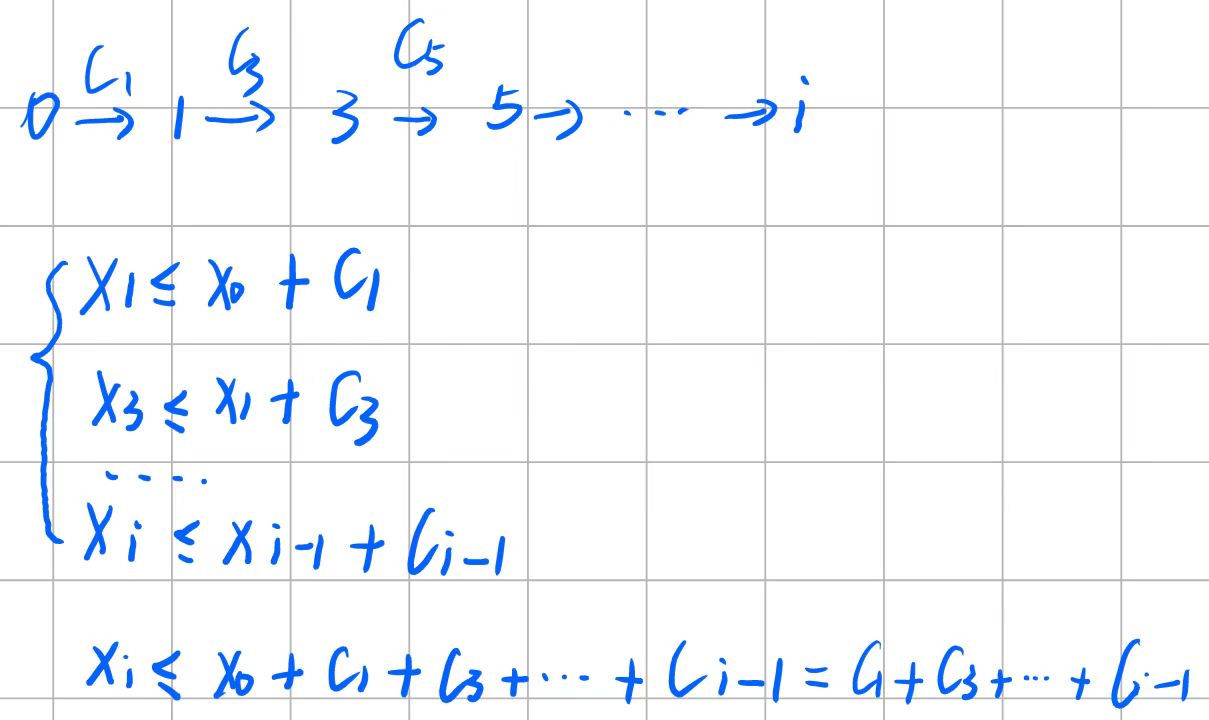
- 方法:建立一个超级源点,0,Xi <= X0 +c,(X0 = 0),建立一条从0到i长度为c的边
糖果
题目描述
幼儿园里有 N
个小朋友,老师现在想要给这些小朋友们分配糖果,要求每个小朋友都要分到糖果。
但是小朋友们也有嫉妒心,总是会提出一些要求,比如小明不希望小红分到的糖果比他的多,于是在分配糖果的时候, 老师需要满足小朋友们的 K
个要求。
幼儿园的糖果总是有限的,老师想知道他至少需要准备多少个糖果,才能使得每个小朋友都能够分到糖果,并且满足小朋友们所有的要求。
输入格式
输入的第一行是两个整数 N,K
。
接下来 K
行,表示分配糖果时需要满足的关系,每行 3
个数字 X,A,B
。
如果 X=1
.表示第 A
个小朋友分到的糖果必须和第 B
个小朋友分到的糖果一样多。
如果 X=2,表示第 A 个小朋友分到的糖果必须少于第 B个小朋友分到的糖果。
如果 X=3,表示第 A个小朋友分到的糖果必须不少于第 B个小朋友分到的糖果。
如果 X=4,表示第 A个小朋友分到的糖果必须多于第 B个小朋友分到的糖果。
如果 X=5,表示第 A个小朋友分到的糖果必须不多于第 B个小朋友分到的糖果。
小朋友编号从 1到 N。
输出格式
输出一行,表示老师至少需要准备的糖果数,如果不能满足小朋友们的所有要求,就输出 −1
。
数据范围
1≤N<105,1≤K≤105,1≤X≤5,1≤A,B≤N,输入数据完全随机。
输入样例:
5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1
输出样例:
11
这道题目我们分析一下
一、我们要求最小值所以要跑最长路,跑最长路的话,我们就需要把不等式的形式变为Xi >= Xj + Ck;
- 第一种关系 A = B 我们可以转换为两组不等式 A >= B, B >= A;
- 第二种关系 A < B 可以转化为 B >= A + 1;
- 第三种关系 A >= B就是我们要的 A >= B;
- 第四中关系 A > B可以转换为 A >= B + 1;
- 第五种关系 A<= B可以转化为 B >= A;
另外我们需要找一个超级源点,使他跑到所有的边这里一半找0号点
我们有另一个隐含的约束条件也就是 Xi >= 1; 也就是说 Xi >= X0 + 1,因为我们超级源点设置为0
这样跑一遍最长路求出来的就是我们要的结果,另外需要注意的是这道题目可能不存在答案,也就是有正环,需要求一下正环,当用队列求正环超时时,我们考虑用栈来优化。
#include<iostream>
#include <cstring>
#include <stack>
using namespace std;
const int N = 1e5 + 10, M = 3 * N;
typedef long long ll;
ll d[N];
bool inq[N];
int cnt[N], n, k;
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c)
{
w[idx] = c; e[idx] = b; ne[idx] = h[a]; h[a] = idx ++;
}
inline bool spfa()
{
stack<int>stk;
memset(d, -0x3f, sizeof d);
d[0] = 0; stk.push(0);inq[0] = 1;
while(stk.size())
{
int t = stk.top(); stk.pop();inq[t] = 0;
for(int i = h[t]; i != - 1; i = ne[i])
{
int j = e[i];
if(d[j] < d[t] + w[i])
{
d[j] = d[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n + 1) return false;
if(!inq[j])
{
inq[j] = 1;
stk.push(j);
}
}
}
}
return true;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> k;
while(k --)
{
int op, a, b;cin >> op >> a >> b;
if(op == 1) add(b, a, 0), add(a, b, 0);
if(op == 2) add(a, b, 1);
if(op == 3) add(b, a, 0);
if(op == 4) add(b, a, 1);
if(op == 5) add(a, b, 0);
}
for(int i = 1; i <= n; ++ i) add(0, i, 1);
if(!spfa()) cout << -1 <<endl;
else
{
ll res = 0;
for(int i = 1; i <= n; ++ i) res += d[i];
cout << res;
}
return 0;
}
4715. 构造数组
请你构造一个长度为 n的正整数数组 a1,a2,…,an。
我们会给出一个长度为 n−1的由 <、>、= 组成的字符串 s1s2…sn−1 用于约束你的构造:
如果 si为 <,则表示你构造的数组需满足 ai<ai+1。
如果 si为 >,则表示你构造的数组需满足 ai>ai+1。
如果 si为 =,则表示你构造的数组需满足 ai=ai+1。
你构造的正整数数组需满足上述约束的同时,保证 a1+a2+…+an的值尽可能小。
请你输出满足条件的正整数数组。
输入格式
第一行包含整数 n。
第二行包含字符串 s1s2…sn−1。
输出格式
共一行,输出 a1,a2,…,an。
数据范围
前 3个测试点满足 2≤n≤6。
所有测试点满足 2≤n≤1000。
输入样例1:
5
><><
输出样例1:
2 1 2 1 2
输入样例2:
5
=<<<
输出样例2:
1 1 2 3 4
这道题求的是最小值所以我们需要把所有关系都转化为Xi >= Xj + Ck的形式然后跑一遍最长路,因为题目中没有说不存在最长路(图中存在正环)的情况,所以默认应该是不存在正环的。
- > > >:ai >= ai+1 + 1,从i + 1到i连一条长度为1的边
- <: ai+1 >= ai + 1,从i到i+1连一条长度为1的边
- =: ai >= ai+1, ai+1 <= ai,连两条边,从i到i+1长度为0的边,从i+1到i长度为1的边
- 另外需要找一个超级源点,使该点能遍历到所有边,这里我们找0点然后1~i所有点都可以用 ai >= 1(题目保证所有的ai都为正整数) ai >= a0 + 1,a0 = 0;所以把0和1~i之间连一条0到i长度为1的边
最后跑一遍最长路就能得到结果
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1010, M = N * 10;
typedef long long ll;
char str[N];
int d[N], n;
bool inq[N];
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c)
{
w[idx] = c; e[idx] = b; ne[idx] = h[a]; h[a] = idx ++;
// cout << a << ' '<< b << ' ' << c << endl;
}
void spfa()
{
queue<int>q;
memset(d, -0x3f, sizeof d);
d[0] = 0;q.push(0);inq[0] = 1;
while(q.size())
{
int t = q.front();q.pop();inq[t] = 0;
for(int i = h[t]; i != -1; i =ne[i])
{
int j = e[i];
if(d[j] < d[t] + w[i])
{
d[j] = d[t] + w[i];
if(!inq[j])
{
inq[j] = 1;
q.push(j);
}
}
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> (str + 1);
for(int i = 1; i <= n - 1; ++ i)
{
if(str[i] == '<') add(i, i + 1, 1);
else if(str[i] == '>') add(i + 1, i, 1);
else if(str[i] == '=') add(i, i + 1, 0), add(i + 1, i, 0);
}
for(int i = 1; i <= n; ++ i) add(0, i, 1);
spfa();
for(int i = 1; i <= n; ++ i) cout << d[i] << ' ';
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署