Derive Modified Gram Schmidt QR Decomposition Algorithm from Gram Schmidt Orthogonalisation (part 2)
All rights reserved. Please don't share this article without notifying me. Email address: westonhunter@zju.edu.cn
From eq. 10 in part 1 we can find the Classical Gram Schmidt Algorithm, which is numerically unstable or sensitive to perturbation:
1 2 3 4 5 6 7 8 9 | Q=zeros((m,n))R=zeros((n,n))for k= 1 to n tmpk=cAk for i= 1 to k-1 R[i][k]=cAk^T*cQi tmpk=tmpk-R[i][k]*cQi R[k][k]=||tmpk|| cQk=tmpk/R[k][k] |
Q calculated by Classical Gram Schmidt algorithm is not very orthogonal due to rounding errors. An example is provided by X. Jiao[1]
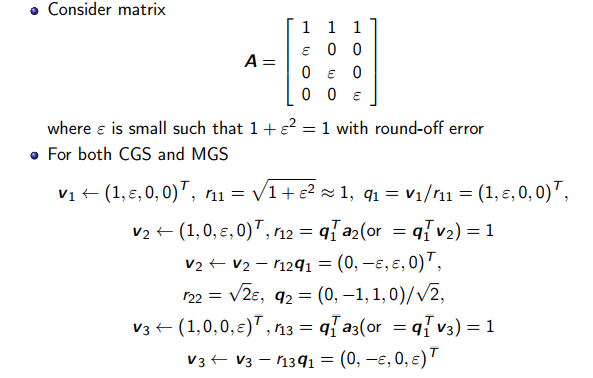
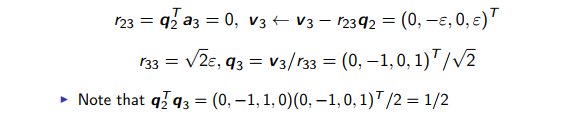
The error introduced in q1 also cause errors in q2 and q3. We will discuss how to avoid this in the next part.
[1] http://www.ams.sunysb.edu/~jiao/teaching/ams526_fall11/lectures/lecture06.pdf



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步