回溯法

一、你对回溯算法的理解

1、定义：回溯法是一种按深度优先的选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新搜索。

2、本质：回溯法本质上就是一种暴力穷举算法，对一个N叉树进行遍历，在前序位置（进入节点时）做出当前选择，然后开始递归，最后在后序位置（离开节点时）撤销当前选择，已维持最终结果的平衡。

3、思考：（1）路径：也就是已经做出的选择。 （2）选择列表：也就是你当前可以做的选择。 （3）结束条件：也就是到达决策树底层，无法再做选择的条件（剪枝）。

4、回溯三部曲：

（1）确定递归函数与参数

（2）递归的终止条件

（3）单层递归逻辑

5、剪枝函数：

   （1）用约束函数在扩展结点处剪去不满足约束的子树；

   （2）用限界函数剪去得不到最优解的子树。

 6、解题模板

回溯算法应用场景：组合、子集、排列、切割、棋盘

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

7、问题树形结构转换

节点为当前状态（包括剩余集合和当前路径），树枝为操作，如：

 

 

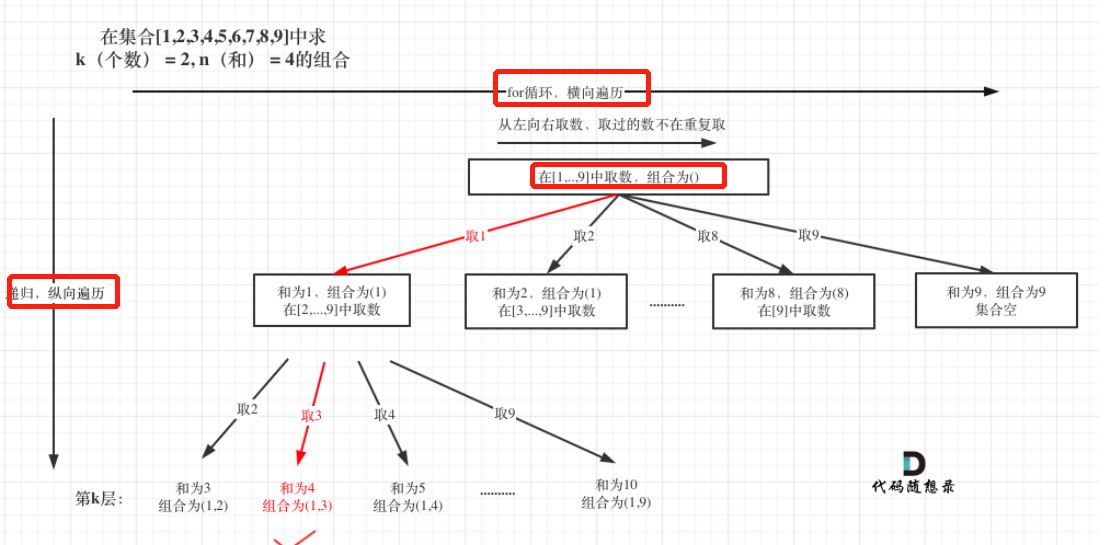
8、常见问题及思路

·排列、组合、子集问题：排列是有顺序的，组合和子集是没有顺序的（因此不同顺序的组合为重复）

（1）元素无重不可复选：①组合：startIndex记录当前已选的下标，确保startIndex前的元素不再选择，下一次递归的startIndex=i+1

                                   ②排列：使用used数组记录已选择的元素，下一次递归时跳过used为true的值

（2）元素无重可复选：组合/排列：递归时加上该层的下标

（3）元素可重不可复选：①组合：排序 + i>startIndex && num[i]==num[i-1]跳过

                                   ②排列：排序 + i>0 && num[i]==num[i-1] && used[i-1]==true（树层去重，树枝不用去重）跳过

·分割问题：类似于组合问题，此时startIndex代表分割的起始位置（或理解为截取哪个下标的元素），而for循环是确定分割的结束位置，结束条件为分割位置遍历到最后。

·子集是收集树形结构中树的所有节点的结果，而组合问题、分割问题是收集树形结构中叶子节点的结果。

·组合问题剪枝（组合个数为k）：i<n-(k-path.length)+1 ,其中n为可选列表总个数、k为组合目标个数

k-path.length表示还需要多少个元素，从后往前看下标最多取到n-(k-path.length)才能取到k个数，+1是因为索引是从1而不是0开始的

8、区别

回溯算法是在遍历树枝，而DFS是在遍历节点