邱锡鹏nndl-chap2_1-线性回归
1.问题描述
有一个函数$f:R\rightarrow R$ ,现在不知道函数 $f(x)$的具体形式,给定满足函数关系的一组训练样本$\left \{ (x_{1},y_{1}),...,(x_{N},y_{N}) \right \}$,N=300,请使用线性回归模型拟合出函数$y=f(x)$。(可尝试一种或几种不同的基函数,如多项式、高斯或sigmoid基函数)
2.数据集
根据某种关系生成的train和test数据。
3.代码实现
3.1载入数据
1 def load_data(filename): 2 """载入数据""" 3 xys = [] 4 with open(filename, 'r') as f: 5 for line in f: 6 xys.append(map(float, line.strip().split())) 7 xs, ys = zip(*xys) 8 return np.asarray(xs), np.asarray(ys) #nsarray将结构数据转换为ndarray类型
3.2不同基函数的实现
对于函数空间中的连续函数都可以表示成一系列基函数的线性组合,就像是在向量空间中每个向量都可以表示成基向量的线性组合一样。
举例:多项式基:{1,t, t2}是实系数二次多项式集合的基,每一个形如a+bt+ct2的二次多项式都可以写成由基函数1、t、t2组成的线性组合。
1 def identity_basis(x): 2 ret = np.expand_dims(x, axis=1) #shape(N, 1) 3 return ret 4 5 6 def multinomial_basis(x, feature_num=10): 7 '''多项式基函数''' 8 x = np.expand_dims(x, axis=1) 9 10 ### START CODE HERE ### 11 feat = [x] 12 for i in range(2, feature_num+1): 13 feat.append(x**i) 14 ret = np.concatenate(feat, axis=1) 15 ### END CODE HERE ### 16 17 return ret 18 19 20 def gaussian_basis(x, feature_num=10): 21 '''高斯基函数''' 22 ### START CODE HERE ### 23 centers = np.linspace(0, 25, feature_num) 24 width = 1.0 * (centers[1] - centers[0]) 25 x = np.expand_dims(x, axis=1) 26 x = np.concatenate([x]*feature_num, axis=1) 27 28 out = (x-centers)/width 29 ret = np.exp(-0.5 * out ** 2) 30 ### END CODE HERE ### 31 32 return ret
3.3训练模型
phi是增广矩阵向量的转置,不同的基函数会形成不同的phi,以identity_basic为例,$phi=\begin{bmatrix}1. & X^{(1)}\\1. & X^{(2)}\\... & \\ 1. & X^{(300)}\end{bmatrix}$
解法1:最小二乘法求解线性回归参数:$w=(XX^{T})^{-1}Xy$ $(XX^{T})^{-1}X$也称为XT的伪逆矩阵
$y=phi*w$
1 def main(x_train, y_train): 2 """ 3 训练模型,并返回从x到y的映射。 4 """ 5 basis_func = identity_basic 6 phi0 = np.expand_dims(np.ones_like(x_train), axis=1) #phi0.shape=(300,1) 7 phi1 = basis_func(x_train) #phi1.shape=(300,1) 8 9 phi = np.concatenate([phi0, phi1], axis=1) #phi.shape=(300,2) phi是增广特征向量的转置 10 11 ### START CODE HERE ### 12 #最小二乘法计算w 13 w = np.dot(np.linalg.pinv(phi), y_train) #np.linalg.pinv(phi)求phi的伪逆矩阵(phi不是列满秩) w.shape=[2,1] 14 ### END CODE HERE ### 15 16 def f(x): 17 phi0 = np.expand_dims(np.ones_like(x), axis=1) 18 phi1 = basis_func(x) 19 phi = np.concatenate([phi0, phi1], axis=1) 20 y = np.dot(phi, w) 21 return y 22 23 return f
解法2:梯度下降求解线性回归参数:$w\leftarrow w+\alpha X(y-X^{T}w)$
详细推导见https://www.cnblogs.com/cxq1126/p/13051607.html
1 def main(x_train, y_train): 2 """ 3 训练模型,并返回从x到y的映射。 4 """ 5 basis_func = identity_basic 6 phi0 = np.expand_dims(np.ones_like(x_train), axis=1) #phi0.shape=(300,1) 7 phi1 = basis_func(x_train) #phi1.shape=(300,1) 8 9 phi = np.concatenate([phi0, phi1], axis=1) #phi.shape=(300,2)phi是增广特征向量的转置 10 11 ### START CODE HERE ### 12 #梯度下降法 13 def dJ(theta, phi, y): 14 return phi.T.dot(phi.dot(theta)-y)*2.0/len(phi) 15 16 def gradient(phi, y, initial_theta, eta=0.001, n_iters=10000): 17 w = initial_theta 18 19 for i in range(n_iters): 20 gradient = dJ(w, phi, y) #计算梯度 21 w = w - eta *gradient #更新w 22 23 return w 24 25 initial_theta = np.zeros(phi.shape[1]) 26 w = gradient(phi, y_train, initial_theta) 27 ### END CODE HERE ### 28 29 def f(x): 30 phi0 = np.expand_dims(np.ones_like(x), axis=1) 31 phi1 = basis_func(x) 32 phi = np.concatenate([phi0, phi1], axis=1) 33 y = np.dot(phi, w) 34 return y 35 36 return f
3.4评估模型
1 def evaluate(ys, ys_pred): 2 """评估模型""" 3 std = np.sqrt(np.mean(np.abs(ys - ys_pred) ** 2)) 4 return std
完整代码如下(使用identity_basis基函数和最小二乘法为例):
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 def load_data(filename): 5 """载入数据""" 6 xys = [] 7 with open(filename, 'r') as f: 8 for line in f: 9 xys.append(map(float, line.strip().split())) 10 xs, ys = zip(*xys) 11 return np.asarray(xs), np.asarray(ys) #nsarray将结构数据转换为ndarray类型 12 13 14 #不同的基函数的实现 15 def identity_basis(x): 16 ret = np.expand_dims(x, axis=1) #shape(N, 1) 17 return ret 18 19 20 def multinomial_basis(x, feature_num=10): 21 '''多项式基函数''' 22 x = np.expand_dims(x, axis=1) 23 24 ### START CODE HERE ### 25 feat = [x] 26 for i in range(2, feature_num+1): 27 feat.append(x**i) 28 ret = np.concatenate(feat, axis=1) 29 ### END CODE HERE ### 30 31 return ret 32 33 34 def gaussian_basis(x, feature_num=10): 35 '''高斯基函数''' 36 ### START CODE HERE ### 37 centers = np.linspace(0, 25, feature_num) 38 width = 1.0 * (centers[1] - centers[0]) 39 x = np.expand_dims(x, axis=1) 40 x = np.concatenate([x]*feature_num, axis=1) 41 42 out = (x-centers)/width 43 ret = np.exp(-0.5 * out ** 2) 44 ### END CODE HERE ### 45 46 return ret 47 48 49 def main(x_train, y_train): 50 """ 51 训练模型,并返回从x到y的映射。 52 """ 53 basis_func = identity_basis 54 phi0 = np.expand_dims(np.ones_like(x_train), axis=1) #phi0.shape=(300,1) 55 phi1 = basis_func(x_train) #phi1.shape=(300,1) 56 57 phi = np.concatenate([phi0, phi1], axis=1) #phi.shape=(300,2)phi是增广特征向量的转置 58 59 ### START CODE HERE ### 60 '''使用最小二乘法计算w''' 61 w = np.dot(np.linalg.pinv(phi), y_train) #np.linalg.pinv(phi)求phi的伪逆矩阵(phi不是列满秩) 62 ### END CODE HERE ### 63 64 def f(x): 65 phi0 = np.expand_dims(np.ones_like(x), axis=1) 66 phi1 = basis_func(x) 67 phi = np.concatenate([phi0, phi1], axis=1) 68 y = np.dot(phi, w) 69 return y 70 71 return f 72 73 74 def evaluate(ys, ys_pred): 75 """评估模型""" 76 std = np.sqrt(np.mean(np.abs(ys - ys_pred) ** 2)) 77 return std 78 79 80 # 程序主入口(建议不要改动以下函数的接口) 81 if __name__ == '__main__': 82 train_file = 'data/train.txt' 83 test_file = 'data/test.txt' 84 # 载入数据 85 x_train, y_train = load_data(train_file) 86 x_test, y_test = load_data(test_file) 87 88 print(x_train.shape) #(300,) 89 print(x_test.shape) #(200,) 90 91 # 使用线性回归训练模型,返回一个函数f()使得y = f(x) 92 f = main(x_train, y_train) 93 94 y_train_pred = f(x_train) 95 std = evaluate(y_train, y_train_pred) 96 print('训练集预测值与真实值的标准差:{:.1f}'.format(std)) 97 98 # 计算预测的输出值 99 y_test_pred = f(x_test) 100 101 # 使用测试集评估模型 102 std = evaluate(y_test, y_test_pred) 103 print('预测值与真实值的标准差:{:.1f}'.format(std)) 104 105 #显示结果 106 plt.plot(x_train, y_train, 'ro', markersize=3) 107 # plt.plot(x_test, y_test, 'k') 108 plt.plot(x_test, y_test_pred, 'k') 109 plt.xlabel('x') 110 plt.ylabel('y') 111 plt.title('Linear Regression') 112 plt.legend(['train', 'test', 'pred']) 113 plt.show()
4.运行结果
以下三张图是分别调用identity_basis、multinomial_basis、gaussian_basis三种不同基函数(最小二乘法计算的w)运行而来。
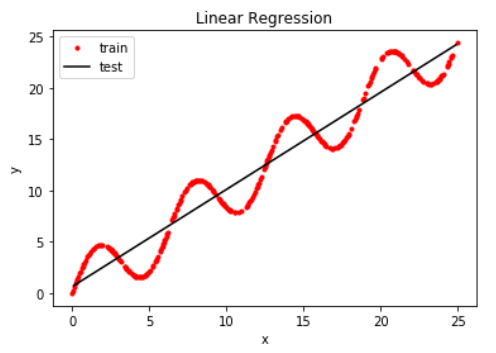
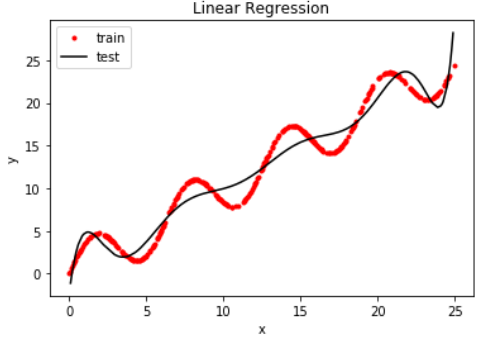
训练集预测值与真实值的标准差:2.0 训练集预测值与真实值的标准差:1.5
预测值与真实值的标准差:2.2 预测值与真实值的标准差:1.6
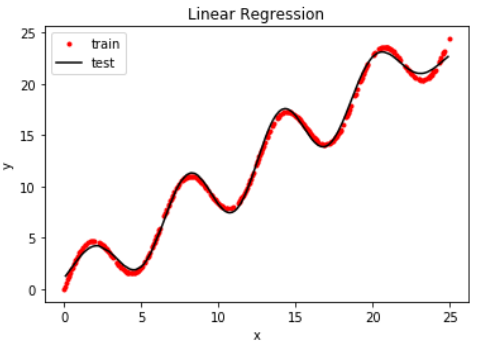
训练集预测值与真实值的标准差:0.4
预测值与真实值的标准差:0.4
以下二张图是分别调用identity_basis、gaussian_basis二种不同基函数(梯度下降法计算的w)运行而来。
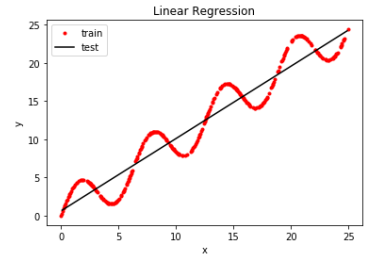
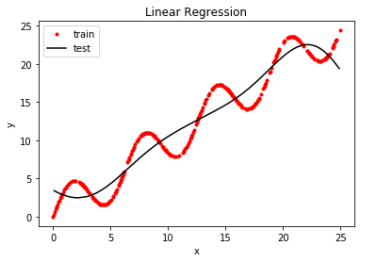
训练集预测值与真实值的标准差:2.0 训练集预测值与真实值的标准差:1.9
预测值与真实值的标准差:2.2 预测值与真实值的标准差:2.1



