信息熵及梯度计算
1.信息熵及梯度计算
热力学中的熵:是表示分子状态混乱程度的物理量
信息论中的熵:用来描述信源的不确定性的大小
经常使用的熵概念有下列几种:
信息熵、交叉熵、相对熵、条件熵、互信息
信息熵(entropy)
信源信息的不确定性函数f通常满足两个条件:
-
是概率p的单调递减函数。
-
两个独立符号所产生的不确定性应等于各自不确定性之和,即f(p1,p2)=f(P1)+f(2)。
对数函数同时满足这两个条件:![]()

信息熵:要考虑信源所有可能发生情况的平均不确定性。若信源符号有n种取值:U1…,Ui…,Un,对应概率为p1…pi…,pn,且各种出现彼此独立。此时信源的平均不确定性应当为单个符号不确定性-logpi的统计平均值(E),称为信息熵,即![]()

交叉熵(cross enytropy)
定义:交叉熵是信息论中一个重要的概念,用于表征两个变量概率分布P,Q(假设P表示真实分布,Q为模型预测的分布)的差异性。交叉熵越大,两个变量差异程度越大。
应用:一般作为神经网络的损失函数用来衡量模型预测的分布和真实分布之间的差异。
交叉熵公式:
相对熵(relative entropy)
也称为KL散度 (Kullback- eibler divergence,简称KLD)、信息散度(information dⅳ ergence)、信息增益((information gain)。
相对熵的定义:是交叉熵与信息熵的差值。表示用分布Q模拟真实分布P,所需的额外信息。
相对熵公式:
举例:
相对熵的性质:
-
相对熵不具有对称性,即DkL(P||Q)≠DkL(Q‖P)。
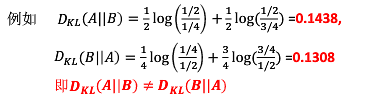
-
相对熵具有非负性。
JS散度(Jensen- Shannon divergence)
JS散度具有对称性:
由于KL散度不具对称性,因此JS散度在KL散度的基础上进行了改进。
现有两个分布p1和p2,其散度公式为:
联合熵(复合熵,Joint Entropy)
-
用H(X,Y)表示
-
两个随机变量X,Y的联合分布的熵,形成联合熵
条件熵(the conditional entropy)
条件熵:H(X|Y)表示在已知随机变量Y的条件下随机变量X的不确定性。
H(X|Y)=H(X,Y)-H(Y),表示(X,Y)的联合熵,减去Y单独发生包含的熵。
推导过程:
-
假设已知y=yj,则
-
对于y的各种可能值,需要根据出现概率做加权平均。即
互信息(Mutual Information)
互信息可以被看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不确定性。
即互信息l(X;Y)是联合分布p(x,y)与乘积分布p(x)p(y)的相对熵
文氏图图解
2.反向传播中的梯度(Gradient in Backpropagation)
反向传播(BP)算法的学习过程由正向传播过程和反向传播过程组成。
反向传播需要通过递归调用链规则( chain rule)计算表达式的梯度。
梯度的简单解释
使用链规则对复合表达式求导
矩阵-矩阵相乘的梯度
需要注意维度和转置操作,例如,D=W*X(W通常表示全局矩阵,X通常表示样本的特征向量矩阵)
3.感知机
感知机是两类分类的线性分类模型。假设输入为实例样本的特征向量x,输出为实例样本的类别y。则由输入空间到输出空间的如下函数称之为感知机。
g为激励函数,以达到对样本分类的目的。
Rosenblatt感知器用阶跃函数作激励函数,其函数公式如下:![]()

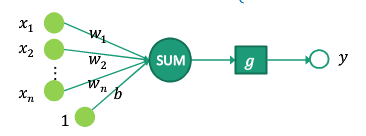
感知机模型的损失函数
感知机模型的优化-随机梯度下降法
感知机学习算法
感知机迭代实例



