特征工程概述
1.特征工程
什么是特征工程?
引自知乎:“数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
深度学习也要用到特征,需要对输入的特征进行组合变换等处理。
自动分词
自动分词就是将用自然语言书写的文章、句段经计算处理后,以词为单位给以输出,为后续加工处理提供先决条件。

词形规范化的两种形式:词根提取与词形还原
- 词根提取( stemming):是抽取词的词干或词根形式(不一定能够表达完整语义)。

- 词形还原( lemmatization):是把词汇还原为一般形式(能表达完整语义)。如将“ drove"处理为"drive"。

词性标注
词性标注(part-of- speech tagging):是指为分词结果中的每个单词标注一个正确的词性的程序,也即确定每个词是名词、动词、形容词或者其他词性的过程。

句法分析
句法分析( Syntactic analysis):其基本任务是确定句子的句法结构或者句子中词汇之间的依存关系。
自然语言处理工具
-
NLTK
Natural Language Toolkit(自然语言处理工具包)是在NLP领域中最常用的一个 Python库。
提供了很多文本处理的功能:
- Tokenization(词语切分,单词化处理)
- Stemming(词干提取)
- Tagging(标记,如词性标注)
- Parsing(句法分析)此外,还提供了50多种语料和词汇资源的接口,如 Word Net等。
-
Text Processing API
支持如下功能:
-
词根提取与词形还原( Stemming& Lemmatization)
-
情感分析( Sentiment Analysis)
-
词性标注和语块抽取( Tagging and chunk Extraction)
-
短语抽取和命名实体识别( Phrase Extraction& Named Entity Recognition)
与NLTK不同,Text Processing API的使用无需安装程序,只需将输入的文本信息通过http post方式联网传递给该网络接口即可。
-
TextBlob工具
-
中文处理工具jieba
功能:分词(包括并行分词、支持自定义词典)、词性标注、关键词提取。
2.向量空间模型和文本相似度计算
文档的向量化表示:BOW假设和VSM模型
为了便于计算文档之间的相似度,需把文档转成统一空间的向量
BOW(bag- of-words model):为了计算文档之间的相似度,假设可以忽略文档内的单词顺序和语法、句法等要素,将其仅仅看作是若干个词汇的集合。
VSM( Vector space model):即向量空间模型。其是指在BOW词袋模型假设下,将每个文档表示成同一向量空间的向量。
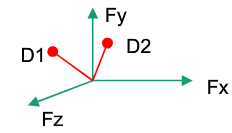
举例:假设有三个文档:
D1:'Jobs was the chairman of Apple Inc, and he was very famous'
D2: 'I like to use apple computer',
D3: 'And I also like to eat apple'
类似这样一批文档的集合,通常也被称为文集或语料(corpus)
上述语料中,共有17个不同的词:
{0:'also';1:'and';2:'apple';3:'chairman';4:'computer';5:'eat';6:'famous';7:'he';8:'inc'; 9:'jobs'; 10:'like';11:'of';12:'the';13:'to';14:'use'; 15:'very';16:'was'.}
因此可构造一个17维的向量空间:
停用词
英文名称: Stop words
停用词通常是非常常见且实际意义有限的词,如英文中“the",“a", "of",“an”等;中文中“的”、“是”、“而且”等。几乎可能出现在所有
场合,因而对某些应用如信息检索、文本分类等区分度不大。在信息检索等应用中,这些词在构建向量空间时通常会被过滤掉。因此这些词也被称为停用词。
Tip:但在某些应用如短语搜索 phrase search中,停用词可能是重要的构成部分,因此要避免进行停用词过滤。
N-gram模型
N-gram通常是指一段文本或语音中连续N个项目(item)的序列。项目(item)可以是单词、字母、碱基对等。
N=1时称为 uni-gram,N=2称为 bi-gram,N=3称为 tri-gram,以此类推。
举例:对于文本 'And I also like to eat apple'
Uni-gram: And, I, also, like, to, eat, apple
Bi-gram: And l, I also, also like, like to, to eat, eat apple
Tri-gram: And I also, I also like, also like to, like to eat, to eat apple
20世纪80年代,N-gram被广泛地应用在拼写检查、输入法等应用中,90年代以后,N-gram得到新的应用,如自动分类信息检索等。即将连续的若干词作为VSM中的维度,用于表示文档。
文档之间的欧式距离
欧氏距离( euclidean metric)是一个通常采用的距离定义,指在n维空间中两个点之间的真实距离。
公式: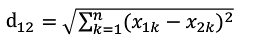
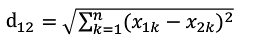
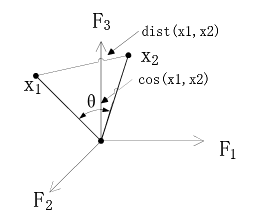
文档之间的余弦相似度(性)
通过计算两个向量的夹角余弦值来评估他们的相似度。余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似。
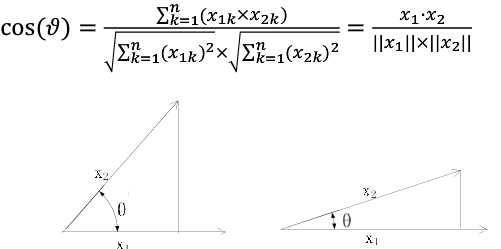
Tf-idf词条权重计算
背景:特征向量里某些高频词在文集内其他文档里面也经常出现。它往往太普遍,对区分文档起的作用不大。
例如:
D1:' Jobs was the chairman of Apple Inc.',
D2: 'I like to use apple computer',
这两个文档都是关于苹果电脑的,则词条 apple对分类意义不大。因此有必要抑制那些在很多文档中都出现了的词条的权重。
在 tf-idf模式下,词条t在文档d中的权重计算为w(t)=tf(t, d)*idf(t)。其中,tf(t,d)表示为词条t在文档d中的出现频率,idf(t)表示与包含词条t的文档数目成反比( inverse document frequency)
idf(t)计算公式: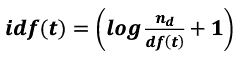 (nd表示文档总数,df(t)表示包含该词条t的文档数)
(nd表示文档总数,df(t)表示包含该词条t的文档数)
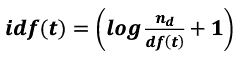 (nd表示文档总数,df(t)表示包含该词条t的文档数)
(nd表示文档总数,df(t)表示包含该词条t的文档数)数据平滑问题:为了防止分母df(t)为零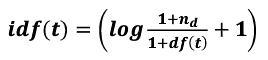
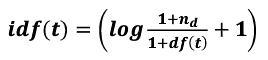
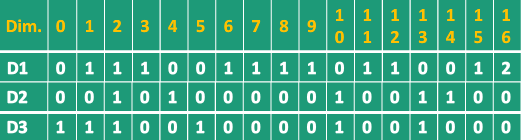
举例:6个文档,3个列

3.特征处理(特征缩放、特征选择及降维)
特征值的缩放
特征值缩放( Feature scaler)也可以称为无量纲处理。主要是对每个列,即同一特征维度的数值进行规范化处理。
应用背景:
-
不同特征(列)可能不属于同一量纲,即特征的规格不一样。例如,假设特征向量由两个解释变量构成,第一个变量值范围[0,1],第二个变量值范围[0,100]。
-
如果某一特征的方差数量级较大,可能会主导目标函数,导致其他特征的影响被忽略。
常用方法:
-
标准化法
前提:特征值服从正态分布
需要计算特征的均值X.mean和标准差X.std: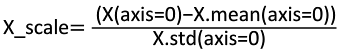
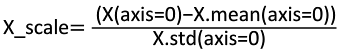
Tip:标准差(Standard Deviation),又称均方差,是方差的算术平方根,用![]()
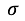 表示。
表示。![]()
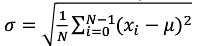
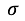 表示。
表示。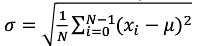
标准差反应一个数据集的离散程度。例如两组数的集合{0,5,9,1,4}和{5,6,8,9}其平均值都是7,但第二个集合具有较小的标准差。
-
区间缩放法
区间缩放法利用了边界值信息,将特征的取值区间缩放到某个特定范围。假设max和min为希望的调整后范围,则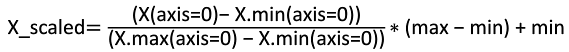
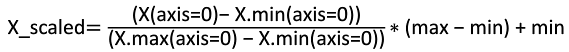
由于希望的调整后范围一般为[0,1]。此时,公式变为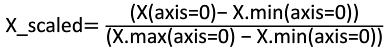
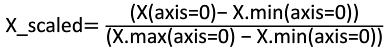
特征值的归一化
归一化是依照特征矩阵的行(即样本)处理数据,其目的在于样本向量在点乘运算或计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”。即使每个样本的范式(norm)等于1。
规则为L1 norm的归一化公式: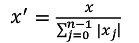
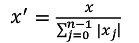
规则为L2 norm的归一化公式: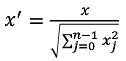
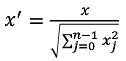
定量特征的二值化
应用背景:对于某些定量特征,需要将定量信息转为区间划分。如将考试成绩转为“及格”或“不及格”
方法:设定一个阈值,大于或者等于阈值的赋值为1,小于阈值的赋值为0,公式表达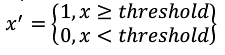
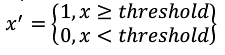
缺失特征值的弥补计算
背景:数据获取时,由于某些原因缺少某些数值,需要进行弥补。
常见的弥补策略:利用同一特征的均值进行弥补。
举例:counts=[[1,0,1],
[2,0,0],
[3,0,0],
[NaN,0,0]],则NaN可以弥补为同列上其他数据的均值,即(1+2+3)/3=2
创建多项式特征
如果基于线性特征的模型不够理想,也可以尝试创建多项式特征。
例如,两个特征(X1,X2),它的平方展开式便转换成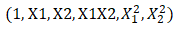 ,也可以自定义选择只保留特征相乘的多项式项。即将特征(X1,X2)转换成(1,X1,X2,X1*X2)。
,也可以自定义选择只保留特征相乘的多项式项。即将特征(X1,X2)转换成(1,X1,X2,X1*X2)。
得到多项式特征后,只是特征空间发生了变化。
特征选择
什么是特征选择?选择对于学习任务(如分类问题)有帮助的若干特征。
为什么要进行特征选择?
-
降维以提升模型的效率
-
降低学习任务难度
-
增加模型的可解释性。
特征选择的角度:
-
特征是否发散:对于不发散的特征,样本在其维度上差异性较小
-
特征与目标的相关性:应当优先选择与目标相关性高的特征
几种常见的特征选择方法:
-
方差选择法
原理:方差非常小的特征维度对于样本的区分作用很小,可以剔除。
例如,假设数据集为布尔特征,想去掉那些超过80%情况下为1或者为0的特征。由于布尔特征是 Bernoulli(伯努利)随机变量,其方差可以计算为Var[x]=p*(1-p),因此阈值为.8*(1-.8)=0.16
 第一列方差为(5/6)*(1/6)=0.14,小于0.16,因此第一列所对应的特征可以被过滤掉。
第一列方差为(5/6)*(1/6)=0.14,小于0.16,因此第一列所对应的特征可以被过滤掉。-
皮尔森相关系数法
皮尔森相关系数( Pearson correlation coefficient)显示两个随机变量之间线性关系的强度和方向。
计算公式为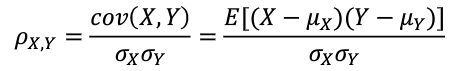
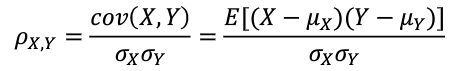
其中,cov(X,Y)表示X和之间的协方差( Covariance),![]()
 是X的均方差,
是X的均方差,![]()
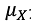 是X的均值,E表示数学期望。
是X的均值,E表示数学期望。
 是X的均方差,
是X的均方差,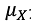 是X的均值,E表示数学期望。
是X的均值,E表示数学期望。计算完毕后,可以将与目标值相关性较小的特征过滤掉。
Tip: Pearson相关系数对线性关系比较敏感。如果关系是非线性的,即便两个变量具有一一对应的关系,Pearso相关性也可能会接近0。
-
基于森林的特征选择法
其原理是某些分类器,自身提供了特征的重要性分值。因此可以直接调用这些分类器,得到特征重要性分值,并排序。
-
递归特征消除法
(以 sklearn中的函数为例)递归特征消除( recursive featureelimination,即RFE)的基本步骤:
-
首先在初始特征或者权重特征集合上训练。通过学习器返回的coef_属性或者 feature_ importances_属性来获得每个特征的重要程度
-
然后最小权重的特征被移除。
-
这个过程递归进行,直到希望的特征数目满足为止。
特征降维
降维本质上是从一个维度空间映射到另一个维度空间。
常见特征降维方法:
-
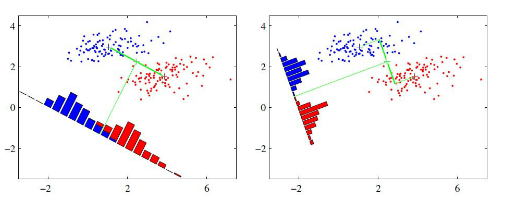
线性判别分析( (Linear Discriminant analysis,简称LDA)是一种监督学习的降维技术,即数据集的每个样本有类别输出。
LDA的基本思想:“投影后类内方差最小,类间方差最大”。即将数据在低维度上进行投影,投影后希望同类数据的投影点尽可能接近,而不同类数据的类别中心之间的距离尽可能的大。
-
主成分分析( principal component analysis)是一种无监督的降维方法。
PCA的基本思想:采用数学变换,把给定的一组相关特征维度通过线性换转成另一组不相关的维度(即 principal components),这些新的维度照方差依次递减的顺序排列:形成第一主成分、第二主成分等。
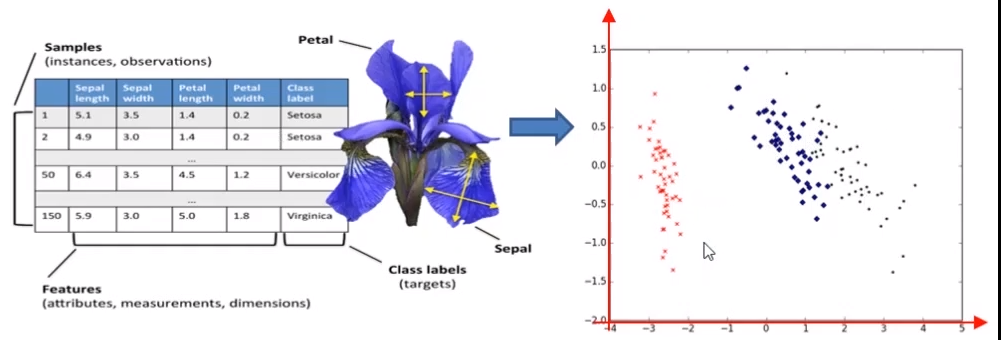
应用:高维数据在二维平面上进行展示。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号