ARC159解题报告
A. Copy and Paste Graph
题意: 给定一个
的邻接矩阵,将其复制 遍(行和列各 个),得到一个 个点的有向图。有 次询问,每次询问 的最短路长度(或不可达)。 。
考察一个点
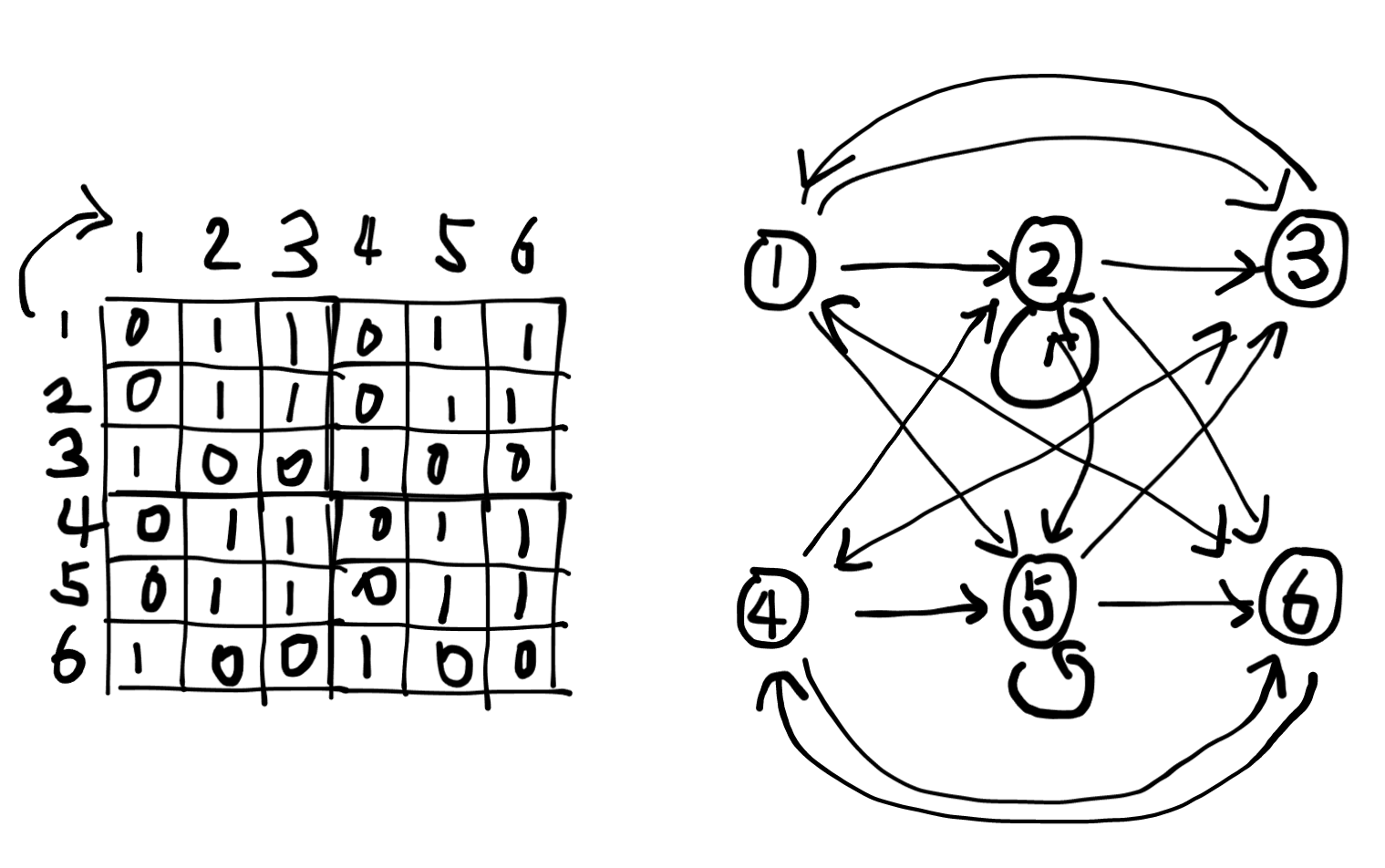
如图所示,复制的
By zhoukangyang
const int N = 107;
ll n, k;
int G[N][N];
int main() {
ios :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> k;
L(i, 1, n) {
L(j, 1, n) {
cin >> G[i][j];
if(G[i][j] == 0)
G[i][j] = 1e9;
}
}
L(k, 1, n)
L(i, 1, n)
L(j, 1, n)
G[i][j] = min(G[i][j], G[i][k] + G[k][j]);
int q;
cin >> q;
while(q--) {
ll x, y;
cin >> x >> y;
x = (x - 1) % n + 1;
y = (y - 1) % n + 1;
if(G[x][y] > n)
cout << -1 << '\n';
else
cout << G[x][y] << "\n";
}
return 0;
}
同样可以每次询问暴力 BFS 求最短路。
By kotatsugame
#include<iostream>
#include<queue>
using namespace std;
int N,K;
int A[100][100];
int dist[100];
int main()
{
cin>>N>>K;
for(int i=0;i<N;i++)for(int j=0;j<N;j++)cin>>A[i][j];
int Q;cin>>Q;
for(;Q--;)
{
long s,t;cin>>s>>t;
s--,t--;
s%=N,t%=N;
for(int i=0;i<N;i++)dist[i]=1e9;
queue<int>Q;
Q.push(s);
while(!Q.empty())
{
int u=Q.front();
Q.pop();
int c=u==s?0:dist[u];
for(int v=0;v<N;v++)if(A[u][v]==1&&dist[v]>c+1)
{
dist[v]=c+1;
Q.push(v);
}
}
int ans=dist[t];
if(ans==(int)1e9)ans=-1;
cout<<ans<<"\n";
}
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步