EDU-CFR-138解题报告
A. Cowardly Rooks
题意：有一个 \(n\times n\) 的棋盘，有 \(m\) 个位置上有车，保证互不攻击。问是否能将一个车移动一次使得仍然互不攻击。
稍加思考可得，如果 \(m\ne n\)，一定可以，否则一定不可以。因为如果 \(m<n\)，则一定有一列是空着的，随便选一辆车移动到该列即可。如果 \(m=n\)，易证一定不可以。
By caoxuanming
#include<bits/stdc++.h>
using namespace std;
signed main() {
int t;
cin>>t;
while(t--) {
int n,m,x,y;
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>x>>y;
if(n==m) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
B. Death's Blessing
题意：有 \(n\) 个怪物排成一排，每个怪物有 \(a_i,b_i\) 两个权值。杀掉一个怪物需要花费 \(a_i\) 的代价，同时会导致与其相邻的怪物的 \(a\) 增加 \(b_i\)。杀掉后左右两边变成相邻的。求全部杀完的最小代价。
我们从贡献的角度考虑。显然每个怪物的 \(a_i\) 都会且仅会给答案造成 \(a_i\) 的贡献，所以可以不用考虑。对于 \(b_i\)，只有杀掉的时候会产生贡献，所以只会贡献一“次”，而每次可以造成 0/1/2 倍的贡献（根据邻居数量）。显然，0 倍贡献只有最后一个怪物可以达到，而其他的怪物要么 1 倍要么 2 倍。此时显然每个其他怪物都用 1 倍更优，而这种方案是一定能够达到的：只需要从两边依次取到最后一个怪物的位置即可。所以只需要让 \(b\) 最大的怪物造成 0 倍，其他造成 1 倍即可。
By caoxuanming
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[200010],b[200010];
signed main() {
int t;
cin>>t;
while(t--) {
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
cin>>b[i];
int maxn=0,sum=0;
for(int i=1;i<=n;i++) {
maxn=max(maxn,b[i]);
sum+=a[i]+b[i];
}
cout<<sum-maxn<<endl;
}
return 0;
}
C. Number Game
题意：有一个长度为 \(n\) 的序列 \(a\)，进行 \(k\) 次操作。第一次操作 Alice 可以删掉一个 \(\le k\) 的数并由 Bob 再删掉一个数（如果没有可以不删）；第二次操作 Alice 可以删掉一个 \(\le k-1\) 的数并由 Bob 再删掉一个数（如果没有可以不删），以此类推直到第 \(k\) 次操作删掉一个 \(\le 1\) 的数。如果在某次操作中 Alice 无数可删则 Bob 赢，否则 Alice赢。问 Alice 能赢的最大的 \(k\)。
显然 \(k\) 不会超过 \(n\)，于是从 \(1\) 到 \(n\) 枚举 \(k\)，每次模拟 \(k\) 次操作即可。贪心地考虑，Alice 每次一定选能选的最大的数删（因为以后可能就没法删了），而 Bob 每次一定选最小的数删（最小的威胁最大，因为更容易被 Alice 删掉）。于是我们在排好序的数组上维护一个双指针即可。
By gyh20
int t,n,m,a[1000002],A,B,R[1000002],stk[1000002],tp;
char s[1000002];
long long ans;
inline bool ck(re int x){
int pos=n;
while(a[pos]>x)--pos;
for(re int i=1;i<=x;++i){
while(a[pos]>x-i+1)--pos;
if(pos<i)return 0;--pos;
}return 1;
}
int main(){
t=read();
while(t--){
n=read();ans=0;
for(re int i=1;i<=n;++i)a[i]=read();sort(a+1,a+n+1);
for(re int i=n;~i;--i)
if(ck(i)){
printf("%d\n",i);
break;
}
}
}
D. Counting Arrays
题意：假设有一个序列 \(a_1\sim a_k\)，我们可以以某种顺序依次删除这 \(k\) 个元素，要求每次删除的数与“当前它所处的位置”互质。问有多少个长度在 \([1,n]\)，值域在 \([1,m]\) 的序列，满足有 \(\ge 2\) 种满足条件的删除方式。
首先，由于任何序列都存在一种平凡的满足条件的删除方式———每次都删除第一个元素，所以问题转化为有多少个序列存在一个非平凡的删除方式。进一步，我们可以发现，如果存在一个 \(2\le j\le i\) 使得 \(a_i\) 与 \(j\) 互质，则一定存在一个非平凡的删除方式：先取若干次第一个元素直到 \(a_i\) 成为第 \(j\) 位，然后取 \(a_i\)，然后再取第一个元素直到取完。反之，如果对于每个 \(i\) 都不存在一个 \(2\le j\le i\) 使得 \(a_i\) 与 \(j\) 互质，则一定不存在非平凡的删除方式，证明显然。
我们可以反向考虑问题，考虑有多少种序列不存在非平凡的删除方式，则每位互相独立。我们只需要对于每个 \(i\)，求出有多少种 \(1\le a_i\le m\) 满足它与任意 \(2\le j\le i\) 都不互质，每位的答案乘起来即可。而一个数与任意 \(2\le j\le i\) 都不互质又可以进一步转化为与任意 \(2\le j\le i,j\text{ is prime}\) 都不互质，即是所有 \(\le i\) 的质数的倍数，也即：是当前所有质数乘积的倍数。所以我们可以维护一个当前质数的乘积 \(now\)，每次更新，答案便乘上 \(m/now\)。由于我们求的是“不存在删除方式”的方案数，而需要求“存在”的方案数，所以真正的答案要用总方案数减去“不存在”的方案数。由于要求长度在 \([1,n]\) 之间，每次扫到一个位就将总答案加上这个位数的答案即可。
By cxm1024
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
bool isprime[300010];
void init() {
int n=300010;
for(int i=0;i<=n;i++)
isprime[i]=1;
isprime[0]=isprime[1]=0;
for(int i=2;i<=n;i++) {
if(!isprime[i]) continue;
for(int j=i*i;j<=n;j+=i)
isprime[j]=0;
}
}
signed main() {
init();
int n,m;
cin>>n>>m;
int now=1,ans=1,ansans=0,mi=1;
for(int i=1;i<=n;i++) {
if(now<=m&&isprime[i]) now=now*i;
(ans*=m/now%mod)%=mod;
mi=mi*(m%mod)%mod;
(ansans+=(mi-ans+mod)%mod)%=mod;
}
cout<<ansans<<endl;
return 0;
}
E. Cactus Wall
题意：有一个 \(n\times m\) 的矩阵，有些位置是有障碍的。你需要添加尽可能少的障碍，满足障碍之间不能边相邻（但可以角相邻，保证初始矩阵满足条件），使得第一行到最后一行不存在路径（不连通）。
我们发现，最终的墙一定是由若干个对角相邻的障碍连起来的。我们可以预处理哪些位置不能放障碍（即与已有障碍相邻的位置），然后预处理这个障碍可以与哪些位置在答案的墙中相邻（即建图），然后问题转化为从第一列到最后一列建一个墙（路径）使得添加的障碍数尽可能少（最短路）。我们可以建一个虚点作为源点连向第一列的所有能放障碍的点，并建一个虚点作为汇点连着最后一列的点，跑一遍 BFS/Dijkstra 即可。
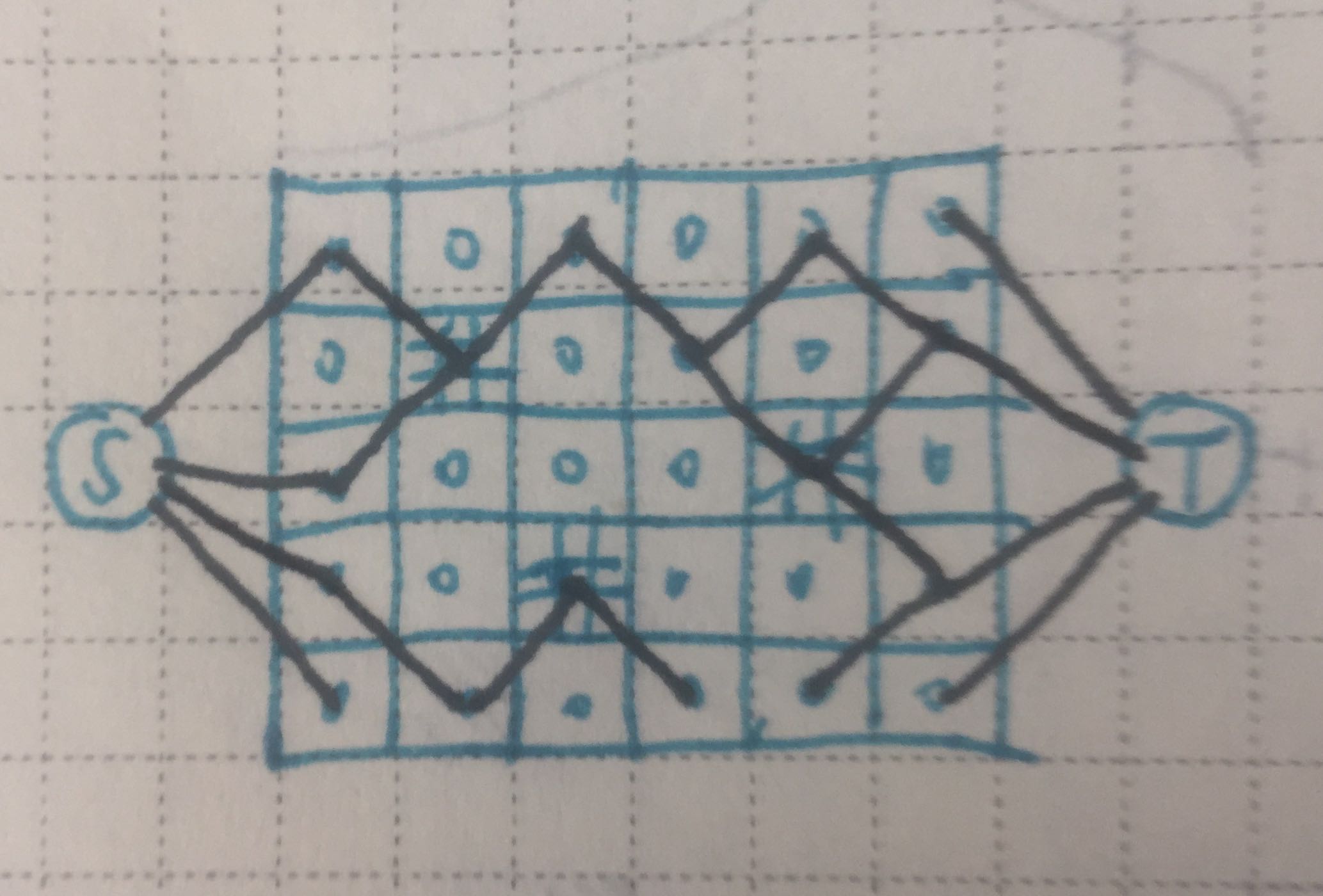
By SSRS_
#include <bits/stdc++.h>
using namespace std;
vector<int> dx = {1, 0, -1, 0};
vector<int> dy = {0, 1, 0, -1};
vector<int> dx2 = {1, 1, -1, -1};
vector<int> dy2 = {1, -1, 1, -1};
const int INF = 100000000;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
for (int i = 0; i < t; i++){
int n, m;
cin >> n >> m;
vector<string> s(n);
for (int j = 0; j < n; j++){
cin >> s[j];
}
vector<vector<bool>> ok(n, vector<bool>(m, true));
for (int j = 0; j < n; j++){
for (int k = 0; k < m; k++){
if (s[j][k] == '#'){
ok[j][k] = false;
for (int l = 0; l < 4; l++){
int x = j + dx[l];
int y = k + dy[l];
if (0 <= x && x < n && 0 <= y && y < m){
ok[x][y] = false;
}
}
}
}
}
vector<vector<int>> d(n, vector<int>(m, INF));
vector<vector<pair<int, int>>> pr(n, vector<pair<int, int>>(m));
deque<tuple<int, int, int>> dq;
for (int j = 0; j < n; j++){
if (s[j][0] == '#'){
d[j][0] = 0;
dq.push_front(make_tuple(0, j, 0));
} else if (ok[j][0]){
d[j][0] = 1;
dq.push_back(make_tuple(1, j, 0));
}
}
while (!dq.empty()){
int c = get<0>(dq.front());
int x = get<1>(dq.front());
int y = get<2>(dq.front());
dq.pop_front();
if (d[x][y] == c){
for (int j = 0; j < 4; j++){
int x2 = x + dx2[j];
int y2 = y + dy2[j];
if (0 <= x2 && x2 < n && 0 <= y2 && y2 < m){
if (s[x2][y2] == '#'){
if (d[x2][y2] > d[x][y]){
d[x2][y2] = d[x][y];
pr[x2][y2] = make_pair(x, y);
dq.push_front(make_tuple(c, x2, y2));
}
}
if (ok[x2][y2]){
if (d[x2][y2] > d[x][y] + 1){
d[x2][y2] = d[x][y] + 1;
pr[x2][y2] = make_pair(x, y);
dq.push_back(make_tuple(c + 1, x2, y2));
}
}
}
}
}
}
int mn = INF, p = -1;
for (int j = 0; j < n; j++){
if (d[j][m - 1] < mn){
mn = d[j][m - 1];
p = j;
}
}
if (p == -1){
cout << "NO" << "\n";
} else {
vector<string> ans = s;
int x = p, y = m - 1;
int CNT = 0;
while (true){
ans[x][y] = '#';
if (y == 0){
break;
}
int x2 = pr[x][y].first;
int y2 = pr[x][y].second;
x = x2;
y = y2;
}
cout << "YES" << "\n";
for (int j = 0; j < n; j++){
cout << ans[j] << "\n";
}
}
}
}
