CSP-S2022解题报告
A. 假期计划
题意:有一个无向图,点有点权。定义两个节点“可达”当且仅当这两个节点的最短路不超过
。求一组互不相同的节点 使得 每步均可达且这四个点的点权和尽可能大。 。
首先跑
#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[2510];
vector<int> a[2510];
bool e[2510][2510];
vector<int> to[2510];
bool vis[2510];
signed main() {
int n,m,kk;
scanf("%lld%lld%lld",&n,&m,&kk);
for(int i=2;i<=n;i++)
scanf("%lld",&v[i]);
for(int i=1;i<=m;i++) {
int x,y;
scanf("%lld%lld",&x,&y);
a[x].push_back(y);
a[y].push_back(x);
}
for(int i=1;i<=n;i++) {
memset(vis,0,sizeof(vis));
queue<pair<int,int> > q;
q.push({i,0});
while(!q.empty()) {
auto u=q.front();q.pop();
if(u.second>kk+1) break;
if(vis[u.first]) continue;
vis[u.first]=1,e[i][u.first]=1;
for(int v:a[u.first])
if(!vis[v]) q.push({v,u.second+1});
}
}
for(int i=2;i<=n;i++) {
for(int j=2;j<=n;j++)
if(i!=j&&e[i][j]&&e[1][j])
to[i].push_back(j);
sort(to[i].begin(),to[i].end(),[&](int x,int y) {
return v[x]>v[y];
});
}
int ans=0;
for(int i=2;i<=n;i++)
for(int j=i+1;j<=n;j++) {
if(!e[i][j]) continue;
for(int k=0;k<min(3ll,(int)to[i].size());k++)
for(int l=0;l<min(3ll,(int)to[j].size());l++)
if(to[i][k]!=j&&to[j][l]!=i&&to[i][k]!=to[j][l])
ans=max(ans,v[i]+v[j]+v[to[i][k]]+v[to[j][l]]);
}
printf("%lld\n",ans);
return 0;
}
B. 策略游戏
题意:给你两个数组
,每次询问 ,进行如下博弈:第一个人先选一个 ,第二个人再选一个 ,其中第一个人想使 最大,第二个人相反。求最终结果。 。
容易发现,此题可以直接分类讨论正负后贪心。如果第一个人选正数,那么第二个人一定会选能选的最小的数。如果第二个人能选到负数则一定会选,此时第一个人选的正数越小越好,否则越大越好。如果第一个人选负数,那么第二个人一定会选最大值。如果第二个人能选到正数则一定会选,此时第一个人选的越大(即越接近
实现上,可以使用线段树维护两个序列的正数最大值、最小值和负数最大值、最小值,每次区间询问合并区间信息即可。
#include<bits/stdc++.h>
using namespace std;
int a[2][100010];
#define mid (t[now].l+t[now].r)/2
#define lson now*2
#define rson now*2+1
struct node {
int l,r,maxp,minp,maxn,minn;
bool havep,haven;
node():havep(0),haven(0){}
};
struct segtree {
node t[400010];
node merge(node x,node y) {
node res;
res.l=x.l,res.r=y.r;
res.havep=(x.havep||y.havep);
res.haven=(x.haven||y.haven);
if(x.havep&&y.havep) {
res.maxp=max(x.maxp,y.maxp);
res.minp=min(x.minp,y.minp);
}
else if(x.havep||y.havep) {
res.maxp=x.maxp*x.havep+y.maxp*y.havep;
res.minp=x.minp*x.havep+y.minp*y.havep;
}
if(x.haven&&y.haven) {
res.maxn=max(x.maxn,y.maxn);
res.minn=min(x.minn,y.minn);
}
else if(x.haven||y.haven) {
res.maxn=x.maxn*x.haven+y.maxn*y.haven;
res.minn=x.minn*x.haven+y.minn*y.haven;
}
return res;
}
void build(int now,int l,int r,bool flag) {
t[now].l=l,t[now].r=r;
if(l==r) {
if(a[flag][l]>=0) {
t[now].havep=1;
t[now].maxp=t[now].minp=a[flag][l];
}
else {
t[now].haven=1;
t[now].maxn=t[now].minn=a[flag][l];
}
return;
}
build(lson,l,mid,flag);
build(rson,mid+1,r,flag);
t[now]=merge(t[lson],t[rson]);
}
node query(int now,int l,int r) {
if(l<=t[now].l&&r>=t[now].r) return t[now];
node res;
if(l<=mid) res=merge(res,query(lson,l,r));
if(r>mid) res=merge(res,query(rson,l,r));
return res;
}
} T1,T2;
void chkmax(long long &x,long long y) {x=(x>y)?x:y;}
int main() {
int n,m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
scanf("%d",&a[0][i]);
for(int i=1;i<=m;i++)
scanf("%d",&a[1][i]);
T1.build(1,1,n,0);
T2.build(1,1,m,1);
while(q--) {
int l1,r1,l2,r2;
scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
node A=T1.query(1,l1,r1);
node B=T2.query(1,l2,r2);
long long ans=-1e18;
if(A.havep) {
if(B.haven) chkmax(ans,1ll*A.minp*B.minn);
else chkmax(ans,1ll*A.maxp*B.minp);
}
if(A.haven) {
if(B.havep) chkmax(ans,1ll*A.maxn*B.maxp);
else chkmax(ans,1ll*A.minn*B.maxn);
}
printf("%lld\n",ans);
}
return 0;
}
C. 星战
题意:有一张简单的有向图(不保证连通),每条边有可用和不可用两种状态,初始每条边都可用。定义一个图是合法的,当且仅当:
- 从每个点开始都存在一个合适的移动方式使得能够无限移动下去。
- 每个点有且仅有一条出边。
你需要进行
次操作,每次如下:
- 给出
,将 变为不可用。保证此前处于可用状态。 - 给出
,将所有 全部变为不可用。 - 给出
,将 变为可用。保证此前处于不可用状态。 - 给出
,将所有 全部变为可用。 每次操作后回答这张图是否合法。
。
可以发现,合法的限制一是没有用的。因为如果满足了限制二,该有向图一定为一个基环内向树森林,于是每个节点必然可以通向一个环。可以通过反证法简单地证明:如果存在某个点不能无限移动下去,设它的终点为
于是问题转化为每次操作后判断是否每个点的出度均为
我们考虑通过哈希来维护这一过程。我们给每个点赋一个随机权值,维护当前每条边起点的权值和
对于暴力连边和断边的操作,可以直接在
- 暴力连断边:根据定义,
- 删点、恢复点:使用
可以感性理解成势能和动能的转化:
#include<bits/stdc++.h>
using namespace std;
long long a[500010],sum[500010],now[500010];
signed main() {
srand(time(0));
int n,m,q;
scanf("%d%d",&n,&m);
long long nowsum=0,all=0;
for(int i=1;i<=n;i++) a[i]=rand(),all+=a[i];
for(int i=1;i<=m;i++) {
int x,y;
scanf("%d%d",&x,&y);
sum[y]+=a[x],now[y]+=a[x],nowsum+=a[x];
}
scanf("%d",&q);
while(q--) {
int op,x,y;
scanf("%d%d",&op,&x);
if(op==1||op==3) scanf("%d",&y);
if(op==1) now[y]-=a[x],nowsum-=a[x];
else if(op==2) nowsum-=now[x],now[x]=0;
else if(op==3) now[y]+=a[x],nowsum+=a[x];
else nowsum+=sum[x]-now[x],now[x]=sum[x];
if(nowsum==all) puts("YES");
else puts("NO");
}
return 0;
}
D. 数据传输
题意:给你一个树,第
个点有点权 ,定义一次跳跃是合法的,当且仅当跳跃的两个节点的距离不超过 。每次询问给出两个节点 ,你需要考虑一个从 走到 的方案 使得每步跳跃都合法。输出经过的点的最小点权和(即 )。 。
首先考虑最简单的
对于
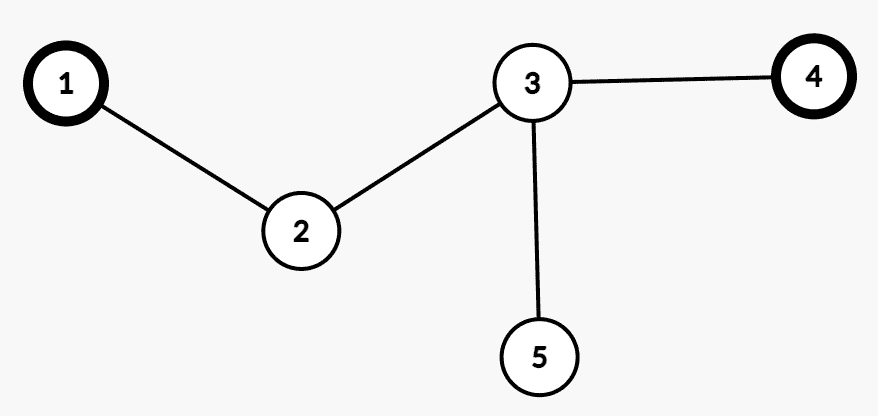
我们可以从
对于
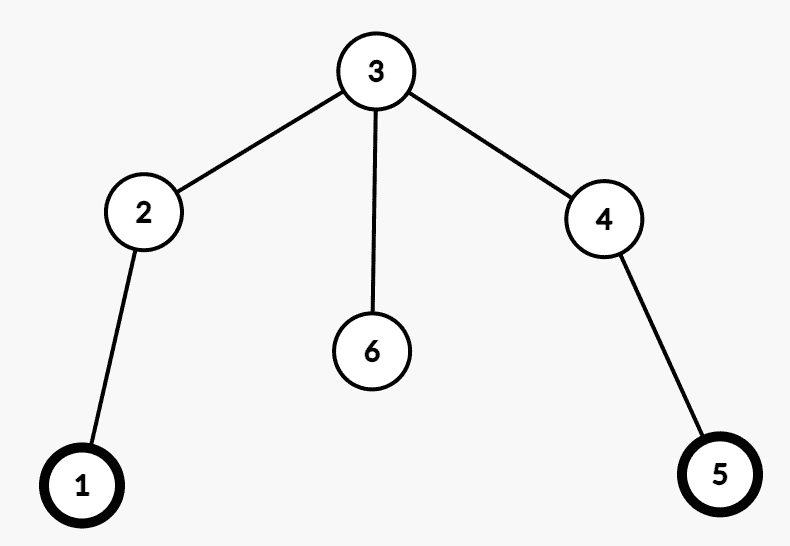
此时如果点
然后我们考虑扩展 DP 状态:定义

此时当前所在的位置有
结合以上分析,我们得到了如下的 DP 方程:
(最后一个为了统一格式也用
这是一个经典的矩阵乘法的定义:内层相加,外层极值。于是,我们可以把 DP 转移转化为下面的矩阵乘法:
在
由于结合律,问题转化为求路径上每个节点的矩阵乘积。由于树上的路径可以分为向上的一段和向下的一段,我们考虑倍增求树上 ST 表。定义
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,q,k,v[200010];
struct matrix {
int n,a[3][3];
matrix operator*(matrix o) {
matrix res;
res.n=n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) {
res.a[i][j]=1e18;
for(int k=0;k<n;k++)
res.a[i][j]=min(res.a[i][j],a[i][k]+o.a[k][j]);
}
return res;
}
} f[200010][20],g[200010][20];
vector<int> e[200010];
int fa[200010][20],mn[200010],dep[200010];
void dfs(int now,int father,int depth) {
fa[now][0]=father,dep[now]=depth;
f[now][0].n=k;
auto &t=f[now][0].a;
for(int i=0;i<3;i++)
t[i][0]=v[now];
t[0][1]=t[1][2]=0;
t[1][1]=mn[now];
t[2][1]=t[0][2]=t[2][2]=1e18;
if(k==2) t[1][1]=1e18;
g[now][0]=f[now][0];
for(int to:e[now])
if(to!=father) dfs(to,now,depth+1);
}
int LCA(int x,int y) {
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--)
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
signed main() {
memset(mn,0x3f,sizeof(mn));
scanf("%lld%lld%lld",&n,&q,&k);
matrix init;
init.n=k;
for(int i=0;i<k;i++)
for(int j=0;j<k;j++)
init.a[i][j]=(i!=j)*1e18;
for(int i=1;i<=n;i++)
scanf("%lld",&v[i]);
for(int i=1;i<n;i++) {
int x,y;
scanf("%lld%lld",&x,&y);
e[x].push_back(y);
e[y].push_back(x);
mn[x]=min(mn[x],v[y]);
mn[y]=min(mn[y],v[x]);
}
dfs(1,0,1);
for(int x=0;x<=19;x++)
f[0][x]=g[0][x]=init;
for(int j=1;j<=19;j++)
for(int i=1;i<=n;i++) {
fa[i][j]=fa[fa[i][j-1]][j-1];
f[i][j]=f[i][j-1]*f[fa[i][j-1]][j-1];
g[i][j]=g[fa[i][j-1]][j-1]*g[i][j-1];
}
while(q--) {
int s,t;
scanf("%lld%lld",&s,&t);
int lca=LCA(s,t),x=v[s];
s=fa[s][0];
matrix tmp1=init,tmp2=init;
for(int i=19;i>=0&&s;i--)
if(dep[fa[s][i]]+1>=dep[lca])
tmp1=tmp1*f[s][i],s=fa[s][i];
for(int i=19;i>=0&&t;i--)
if(dep[fa[t][i]]>=dep[lca])
tmp2=g[t][i]*tmp2,t=fa[t][i];
matrix ans=tmp1*tmp2;
printf("%lld\n",ans.a[0][0]+x);
}
return 0;
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步