CF杂题题解

862B. Mahmoud and Ehab and the bipartiteness

题意：给你一棵树（显然是二分图），问最多能添加多少条边使得仍然保持二分图性质。

直接二分图染色，奇数层在一边，偶数层在另一边。得到两边的点数，相乘即为最多有多少条边，减去 \(n-1\) 即可。

{% note success code %}

const int N=1e5+10;
int n;
VI e[N];
LL c[2];
void dfs( int p, int f, int d ) {
    c[d]++;
    for ( int i:e[p] ) if ( i!=f ) dfs(i,p,d^1);
}
int main() {
    R(n);
    REP(i,n-1) {
        int a,b;
        R(a,b);
        e[a].PB(b);
        e[b].PB(a);
    }
    dfs(1,0,0);
    LL ans=c[0]*c[1]-(n-1);
    W(ans);
    return 0;
}

{% endnote %}

1676G. White-Black Balanced Subtrees

题意：有根树上每个节点非黑即白，问有多少棵子树满足黑节点数量等于白节点数量。

DFS 即可，返回子树内黑白节点数量，递归往上合并。

{% note success code %}

By Joshc

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mp make_pair
#define pii pair<int, int>
#define f first
#define s second
const int MOD = 1000000007;
vector<int> edges[4005];
char c[4005];
int ans = 0;
int dfs(int v) {
    int cur = (c[v] == 'B' ? 1 : -1);
    for (int i : edges[v]) cur += dfs(i);
    ans += cur == 0;
    return cur;
}
void solve() {
    int n, x;
    scanf("%d", &n);
    for (int i=1; i<=n; i++) edges[i].clear();
    for (int i=2; i<=n; i++) {
        scanf("%d", &x);
        edges[x].push_back(i);
    }
    for (int i=1; i<=n; i++) scanf(" %c", &c[i]);
    ans = 0;
    dfs(1);
    printf("%d\n", ans);
}
int main() {
    int tests = 1;
    scanf("%d", &tests);
    while (tests--) solve();
}

{% endnote %}

164A. Variable, or There and Back Again

题意：一个有向图由 0、1、2 三种点组成，对于每个点判断是否存在一条经过该点的路径（不一定是简单路径），满足起点为 1 型点、终点为 2 型点且中间没有 1 型点（可以有 2 型点）。

做法 1（正解）

转换一下题目要求：对于每个点判断是否存在一个 1 型点能到达此点且能“在不经过 1 型点的情况下”到达一个 2 型点。

对于前者，可以直接从每个 1 型点 DFS，将能到达的点打上标记；对于后者，再转换一下限制：存在一个 2 型点，能在不经过 1 型点的情况下到达该点。于是对于后者，在反向图上从每个 2 型点开始 DFS 打标记，遇到 1 型点时直接 return 即可。

{% note success code %}

By dzhulgakov

#define N 111000
int n,m,f[N];
bool mark[N],bmark[N];
VI adj[N],badj[N];

void dfs1(int v)
{
	if (mark[v]) return;
	mark[v] = true;
	REP(i,SZ(adj[v])) dfs1(adj[v][i]);
}

void dfs2(int v)
{
	if (bmark[v]) return;
	bmark[v] = true;
	if (f[v] == 1) return;
	REP(i,SZ(badj[v])) dfs2(badj[v][i]);
}

int main()
{
	scanf("%d%d",&n,&m);
	REP(i,n)
		scanf("%d",f+i);
	REP(i,m)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		--x;--y;
		adj[x].pb(y);
		badj[y].pb(x);
	}
	CLEAR(mark);
	CLEAR(bmark);
	REP(i,n) if (!mark[i] && f[i]==1) dfs1(i);
	REP(i,n) if (!bmark[i] && f[i]==2) dfs2(i);
	REP(i,n)
		printf(" %d"+(i==0),mark[i]&&bmark[i] ? 1 : 0);
	printf("\n");
	return 0;
}

{% endnote %}

做法 2（错解）

直接从每个 1 型点 DFS，碰到新的 1 型点时直接 return，如果有 2 型点则回溯的时候打上标记。

{% note danger code %}

#include<bits/stdc++.h>
using namespace std;
int c[100010];
vector<int> a[100010];
bool vis[100010],ans[100010];
int root;
bool dfs(int now) {
	if(now!=root&&c[now]==1) return 0;
	if(vis[now]) return ans[now];
	vis[now]=1;
	if(c[now]==2) ans[now]=1;
	for(int v:a[now])
		ans[now]|=dfs(v);
	return ans[now];
}
signed main() {
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>c[i];
	for(int i=1;i<=m;i++) {
		int u,v;
		cin>>u>>v;
		a[u].push_back(v);
	}
	for(int i=1;i<=n;i++)
		if(c[i]==1)
			root=i,dfs(i);
	for(int i=1;i<=n;i++)
		cout<<ans[i]<<endl;
	return 0;
}

{% endnote %}

这样的做法错在哪里呢？

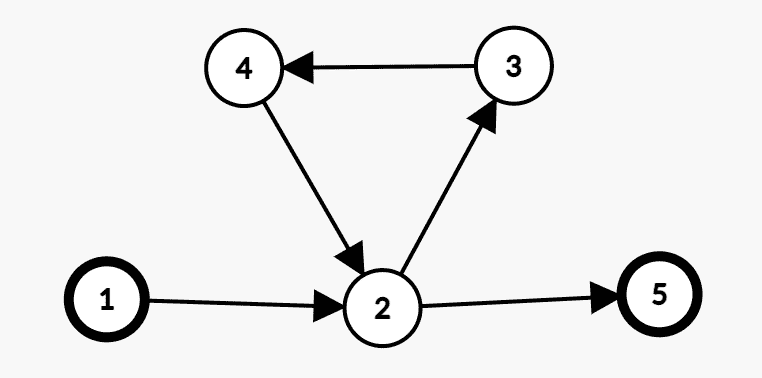
在上图的情况中，1 为 1 型点，5 为 2 型点，则显然的一条路径为 \(1\to 2\to 3\to 4\to 5\)。然而在 DFS 时，我们先搜到 2，打上了 \(vis\) 标记，走完 3、4 再次到 2 时，由于已经有了 \(vis\) 标记，程序认为它已经搜完了，于是直接返回了 0，认为 2 没法到达 2 型点。但实际上并不是没法到达，而是还没搜到。当我们回溯到 2 时，再向 5 搜，虽然可以找到 \(1\to 2\to 5\) 这条路径，但 3 和 4 的答案就定在了“无法到达”上。做法 1 就完全不会遇到这种问题。

698B. Fix a Tree

题意：一棵树可以用一个序列 \(p\) 表示。具体地，任选一个根 \(x\)，当 \(i\ne x\) 时 \(p_i\) 为 \(i\) 节点的父亲，当 \(i=x\) 时 \(p_i=i\)。一棵树转换成序列的方式并不唯一。定义一个序列是合法的，当且仅当存在一棵树可以表示成该序列。给定初始序列 \(a\)，问至少修改多少个元素使得该序列合法，并输出修改后的序列。

注意到，初始的 \(a\) 序列如果按照 \(i\to a_i\) 连边，会形成一个基环树森林。对于每个基环树，必然要选择环上一个点断掉一条环上的边，最后连接起来。如果存在一棵基环树的环为一个点的自环，则该点可以为树的根，无需修改。找环的操作可以用 DFS 完成，对于自环特判一下即可。

{% note success code %}

By MiracleFaFa

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <cassert>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1000000007;
ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
// head

const int N=201000;
int n,p[N],vis[N],rt,cnt,T;
int main() {
	scanf("%d",&n);
	rep(i,1,n+1) {
		scanf("%d",p+i);
		if (p[i]==i) rt=i;
	}
	rep(i,1,n+1) if (!vis[i]) {
		T++;
		int x=i;
		while (!vis[x]) {
			vis[x]=T;
			x=p[x];
		}
		if (vis[x]==T) {
			if (!rt) {
				rt=x; p[x]=x;
				cnt++;
			}
			if (x!=rt) {
				p[x]=rt;
				cnt++;
			}
		}
	}
	printf("%d\n",cnt);
	rep(i,1,n+1) printf("%d ",p[i]);
}

{% endnote %}

代码细节：使用循环代替了 DFS 找环的过程。

216B. Forming Teams

题意：有一个无向图（不一定连通），每个点的度数不超过 \(2\)，问最少删除多少个点，才能使得该图成为二分图且两边的点数相同。

由于每个点的度数不超过 \(2\)，图一定有若干个环和若干条链组成。对于长度为偶数的环和长度为偶数的链，本身满足条件，可以不用考虑。对于奇数环，必须删掉一个点转换成偶数链，此时直接 ans++。对于奇数链，本身是二分图但两侧节点数差 \(1\)，所以两个奇数链的差可以抵消。如果有奇数条奇数链，ans++，否则 ans 不变。环和链的判断可以 DFS 完成。

{% note success code %}

By dreamoon_love_AA

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
vector<int>e[111];
int used[111],cnt,cnt2;
void dfs(int x){
    used[x]=1;
    cnt+=e[x].size();
    cnt2++;
    for(int i=0;i<e[x].size();i++)
        if(used[e[x][i]]==0)dfs(e[x][i]);
}
int main(){
    int i,j,k,n,m,stop=0;
    scanf("%d%d",&n,&m);
    for(i=0;i<m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        e[x].pb(y);
        e[y].pb(x);
    }
    for(i=1;i<=n;i++){
        if(!used[i]){
            cnt=0;
            cnt2=0;
            dfs(i);
            if(cnt2%2==1&&cnt2*2==cnt){
                stop++;
            }
        }
    }
    printf("%d\n",stop+(n-stop)%2);
    return 0;
}

{% endnote %}

代码细节：通过 \(cnt\) 和 \(cnt2\) 的记录巧妙地判断是环还是链。

1714G. Path Prefixes

题意：一棵以 \(1\) 为根的有根树，每个边 \(i\) 有两个边权 \(a_i\) 和 \(b_i\)。对于每个点 \(i\)，令 \(p_1\sim p_k\) 表示从根节点到 \(i\) 的边的序列，求最长的 \(r_i\) 使得 \(\sum\limits_{j=1}^{r_i} b_{p_j}\le\sum\limits_{j=1}^k a_{p_j}\)。

DFS 是维护根到当前点的 \(a\) 边权总和以及 \(b\) 边权前缀和 \(s\)，每次在 \(s\) 中查找即可。

{% note success code %}

By tourist

#include <bits/stdc++.h>

using namespace std;

#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif

int main() {
  ios::sync_with_stdio(false);
  cin.tie(0);
  int tt;
  cin >> tt;
  while (tt--) {
    int n;
    cin >> n;
    vector<vector<array<int, 3>>> g(n);
    for (int y = 1; y < n; y++) {
      int x, w0, w1;
      cin >> x >> w0 >> w1;
      --x;
      g[x].push_back({y, w0, w1});
      g[y].push_back({x, w0, w1});
    }
    vector<long long> seq(1, 0);
    vector<int> res(n);
    function<void(int, int, long long)> Dfs = [&](int v, int pr, long long s) {
      if (v > 0) {
        res[v] = (int) (lower_bound(seq.begin(), seq.end(), s + 1) - seq.begin()) - 1;
      }
      for (auto& p : g[v]) {
        int u = p[0];
        if (u == pr) {
          continue;
        }
        seq.push_back(seq.back() + p[2]);
        Dfs(u, v, s + p[1]);
        seq.pop_back();
      }
    };
    Dfs(0, -1, 0);
    for (int i = 1; i < n; i++) {
      cout << res[i] << " \n"[i == n - 1];
    }
  }
  return 0;
}

{% endnote %}

813C. The Tag Game

题意：Alice 和 Bob 在一棵树上博弈，初始时 Alice 在 \(1\) 节点（根节点），Bob 在 \(x\) 节点。二人轮流沿边走，Bob 先走，每回合可以不走。Alice 希望尽快抓到 Bob 而 Bob 相反。问最终的回合数。

显然 Alice 可以只由浅向深走而保证抓到 Bob，此时回合最少。所以 Bob 的任务为在保证不被抓到的前提下前往尽可能深的点待着不动。

做法 1

可以先跑两遍 DFS 得出每个点与 Alice 和 Bob 的距离（与 Alice 的距离即为深度）。每个与 Bob 距离比与 Alice 距离近的点都是 Bob 能够安全到达的，所以取这些点中深度最深的即可。

{% note success code %}

By Avason

#include <bits/stdc++.h>
#define int long long
using namespace std;
vector <int> e[200005];
int depa[200005],depb[200005];
inline void dfsa(int u,int f)
{
	for(auto v:e[u])
		if(v!=f) depa[v]=depa[u]+1,dfsa(v,u);
}
inline void dfsb(int u,int f)
{
	for(auto v:e[u])
		if(v!=f) depb[v]=depb[u]+1,dfsb(v,u);
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n,B;
	cin >> n >> B;
	for(int i=1;i<n;i++)
	{
		int u,v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfsa(1,0);
	dfsb(B,0);
	int mx=0,ans=0;
	for(int i=1;i<=n;i++)
	{
		if(depa[i]>depb[i])
		{
			ans=max(ans,depa[i]*2);
		}
	}
	cout << ans;
	return 0;
}

{% endnote %}

做法 2

如果 Bob 在一个点没被抓到，那么他往下走也不会被抓到，所以在不被抓到的前提下，Bob 可以先尽可能地往上走获得后续的更多选择。找到能到达的最上面的点时，再找该子树下深度最深的点即可。

{% note success code %}

By fqw

vector<VI> es;
VI d, f, fat;
int n;

void dfs(int x, int fa, int dep) {
    d[x] = dep, f[x] = dep;
    fat[x] = fa;
    for(int y : es[x]) {
        if(y != fa) {
            dfs(y, x, dep + 1);
            setmax(f[x], f[y]);
        }
    }
}

int main() {
    int x;
    scanf("%d%d", &n, &x);
    --x;
    es.resize(n);
    d.resize(n);
    f.resize(n);
    fat.resize(n);
    repn(i, n - 1) {
        int a, b;
        scanf("%d%d", &a, &b);
        --a, --b;
        es[a].pb(b), es[b].pb(a);
    }
    dfs(0, -1, 0);
    int dt = d[x] / 2 + 1;
    while(d[x] > dt) x = fat[x];
    printf("%d\n", f[x] * 2);

    return 0;
}

{% endnote %}

691D. Swaps in Permutation

题意：有一个排列和 \(m\) 个操作，每个操作 \((a_i,b_i)\) 表示交换排列的第 \(a_i\) 个元素和第 \(b_i\) 个元素。你可以以任意顺序进行操作任意多次，问操作后的最大字典序。

显然交换具有传递性，即若 \(a_1,a_2\) 可以交换、\(a_2,a_3\) 可以交换，则 \(a_1,a_2,a_3\) 可以任意排列。于是将每个 \((a_i,b_i)\) 连边，每个连通块内都可以任意排列，显然从大到小排列输出即可。

{% note success code %}

By I_love_Tanya_Romanova

int n, k, ar[N];
vector<int> vec[N];
int w[N];

int get(int x)
{
	if (w[x] == x)
		return x;
	return w[x] = get(w[x]);
}

void merge(int a, int b)
{
	a = get(a);
	b = get(b);
	w[a] = b;
}

int ans[N];

int main(){
	//freopen("fabro.in","r",stdin);
	//freopen("fabro.out","w",stdout);
	//freopen("F:/in.txt", "r", stdin);
	//freopen("F:/output.txt", "w", stdout);
	ios_base::sync_with_stdio(0);
	//cin.tie(0);

	cin >> n >> k;
	for (int i = 1; i <= n; i++)
	{
		cin >> ar[i];
	}

	for (int i = 1; i <= n; i++)
		w[i] = i;

	for (int i = 1; i <= k; i++)
	{
		int a, b;
		cin >> a >> b;
		merge(a, b);
	}

	for (int i = 1; i <= n; i++)
	{
		int id = get(i);
		vec[id].push_back(ar[i]);
	}

	for (int i = 1; i <= n; i++)
		sort(vec[i].begin(), vec[i].end());

	for (int i = 1; i <= n; i++)
	{
		int id = get(i);
		int val = vec[id].back();
		vec[id].pop_back();
		ans[i] = val;
	}

	for (int i = 1; i <= n; i++)
	{
		if (i > 1)
			cout << " ";
		cout << ans[i];
	}
	cout << endl;

	cin.get(); cin.get();
	return 0;
}

{% endnote %}

1722F. L-shapes

题意：一个 \(L\) 形如下所示
*.  .*  **  **
**  **  *.  .*
给你一个 \(n\times m\) 的矩阵，问能否由若干个 \(L\) 形拼成且每个 \(L\) 形不相交、不共边、不共定点。

可以搜索得到八连通的连通块，如果块的大小不为 \(3\) 则直接输出 No，如果为 \(3\) 则判断是否为 \(L\) 形。

{% note success code %}

By wtmoo: kevinyang, uwu

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
bool good(int x, int y){
	if(1<=x&&x<=n&&y>=1&&m>=y)return true;
	return false;
}
signed main(){
	cin.tie(nullptr)->sync_with_stdio(false);
	int t;
	cin >> t;
	while(t--){
		cin >> n >> m;
		vector<vector<char>>mp(n+1,vector<char>(m+1));
		for(int i = 1; i<=n; i++){
			string s;
			cin >> s;
			for(int j = 1; j<=m; j++){
				mp[i][j] = s[j-1];
			}
		}
		vector<int>dx = {-1,0,1,0,1,1,-1,-1};
		vector<int>dy = {0,1,0,-1,-1,1,1,-1};
		bool f = true;
		vector<vector<bool>>vis(n+1,vector<bool>(m+1));
		for(int i = 1; i<=n; i++){
			for(int j = 1; j<=m; j++){
				queue<pair<int,int>>q;
				if(vis[i][j])continue;
				if(mp[i][j]!='*')continue;
				q.push({i,j});
				vis[i][j] = true;
				set<int>sx;
				set<int>sy;
				sx.insert(i);
				sy.insert(j);
				int cnt = 1;
				while(q.size()){
					pair<int,int>cur = q.front(); q.pop();
					int x = cur.first; int y = cur.second;
					for(int d = 0; d<8; d++){
						int nx = x+dx[d];
						int ny = y+dy[d];
						if(!good(nx,ny))continue;
						if(vis[nx][ny])continue;
						if(mp[nx][ny]=='.')continue;
						q.push({nx,ny});
						sx.insert(nx); sy.insert(ny);
						vis[nx][ny] = true;
						cnt++;
					}
				}
				if(cnt==3&&sx.size()==2&&sy.size()==2)continue;
				f = false;
			}
		}
		if(f)cout << "YES\n";
		else cout << "NO\n";
	}
	return 0;
}

{% endnote %}

29C. Mail Stamps

题意：有一个 \(n\) 个点的链，给你 \(n-1\) 条边，按顺序输出链上的点。点的下标在 \([1,10^9]\) 内。

离散化，暴力循环输出即可。

{% note success code %}

By Farhod_Farmon

#include <bits/stdc++.h>

#define fi first
#define se second
#define sc scanf
#define pr printf
#define pb push_back
#define mp make_pair
#define fin(s) freopen( s, "r", stdin );
#define fout(s) freopen( s, "w", stdout );

const int N = 100100;

using namespace std;

int n;
vector < int > v[N], ans;
map < int, int > rv, us;

void dfs(int x, int p)
{
    ans.pb(x);
    for(int i = 0; i < v[x].size(); i++)
        if(v[x][i] != p)
            dfs(v[x][i], x);
}

int main()
{
    //fin("input.txt");
    //fout("output.txt");
    ios_base::sync_with_stdio(0);
    cin >> n;
    int g = 0;
    for(int i = 1; i <= n; i++){
        int x, y;
        cin >> x >> y;
        if(us.find(x) == us.end()){
            us[x] = ++g;
            rv[g] = x;
        }
        if(us.find(y) == us.end()){
            us[y] = ++g;
            rv[g] = y;
        }
        x = us[x];
        y = us[y];
        v[x].pb(y);
        v[y].pb(x);
    }
    int root = 1;
    for(int i = 1; i <= g; i++)
        if(v[i].size() == 1)
            root = i;
    dfs(root, -1);
    for(int i = 0; i < ans.size(); i++)
        cout << rv[ans[i]] << " ";
}

{% endnote %}

213A. Game

题意：有三个电脑和 \(n\) 个游戏，第 \(i\) 个游戏需要在第 \(c_i\) 个电脑上完成，游戏之间有依赖关系但保证没有环。完成每个游戏需要一小时，在电脑之间移动 \(1\to 2,2\to 3,3\to 1\) 需要一小时，\(3\to 2,2\to 1,1\to 3\) 需要两小时。初始可以选择在任意电脑前，问完成全部游戏的最少时间。

注意到在电脑之间移动时，\(+1 \mod 3\) 花费 \(1\) 而 \(-1 \mod 3\) 花费 \(2\)，所以一定不会出现 \(-1 \mod 3\)（最差也可以用两次 \(+1 \mod 3\) 代替）。所以只需要每次贪心地将当前电脑能玩的全部玩完再到下一个电脑即可。需要分类讨论初始位置。

{% note success code %}

By eddy1021

int n , c[ N ] , ind[ N ];
vector< int > v[ N ];
void init(){
  n = getint();
  for( int i = 1 ; i <= n ; i ++ )
    c[ i ] = getint() - 1;
  for( int i = 1 ; i <= n ; i ++ ){
    ind[ i ] = getint();
    for( int j = 0 ; j < ind[ i ] ; j ++ ){
      int fr = getint();
      v[ fr ].push_back( i );
    }
  }
}
vector<int> q[ 3 ];
int tind[ N ];
int go( int st , int nxt ){
  for( int i = 0 ; i < 3 ; i ++ )
    q[ i ].clear();
  for( int i = 1 ; i <= n ; i ++ ){
    tind[ i ] = ind[ i ];
    if( ind[ i ] == 0 )
      q[ c[ i ] ].push_back( i );
  }
  int gt = 0 , ret = 0;
  while( gt < n ){
    while( q[ st ].size() ){
      int who = q[ st ].back();
      q[ st ].pop_back();
      gt ++;
      ret ++;
      for( auto tmp : v[ who ] ){
        tind[ tmp ] --;
        if( tind[ tmp ] == 0 ){
          q[ c[ tmp ] ].push_back( tmp );
        }
      }
    }
    if( gt == n ) break;
    ret ++;
    st = ( st + nxt + 3 ) % 3;
  }
  return ret;
}
void solve(){
  int ans = N * N;
  for( int st = 0 ; st < 3 ; st ++ )
    ans = min( ans , go( st , 1 ) );
  printf( "%d\n" , ans );
}
int main(){
  build();
  //__ = getint();
  while( __ -- ){
    init();
    solve();
  }
}

{% endnote %}

408B. Garland

题意：有一些颜色的纸若干张，每张面积为 \(1\)，你需要拼成一定的彩带，要求每个位置的颜色对应。你可以将纸剪开，但不能拼起来。问最多能有多大面积或回答无法拼成。

显然对于每种颜色单独考虑。一种颜色如果纸比目标多，那一定是目标的面积。如果比目标少，则可以全部用上。所以答案为二者取 \(\min\)。

做法 1

做法 2

做法 1

做法 2

做法 1（正解）

做法 2（错解）

做法 1

做法 2

公告