ABC274F-Fishing题解

题目传送门

题意：有 \(n\) 条鱼在数轴上，第 \(i\) 条鱼初始在 \(x_i\)，有一个向右的速度 \(v_i\) 以及全职 \(w_i\)。问任选出一个时刻 \(t\) 并选出一个长度为 \(A\) 的区间，包含的鱼的权值和最大为多少。\(n\le 2000,\text{other val}\le 10^4\)。

可以考虑枚举最左边选哪条鱼，设为第 \(i\) 条，例如 \(x_i=1,v_i=2,A=1\)，则其他我们可以画出两条直线：

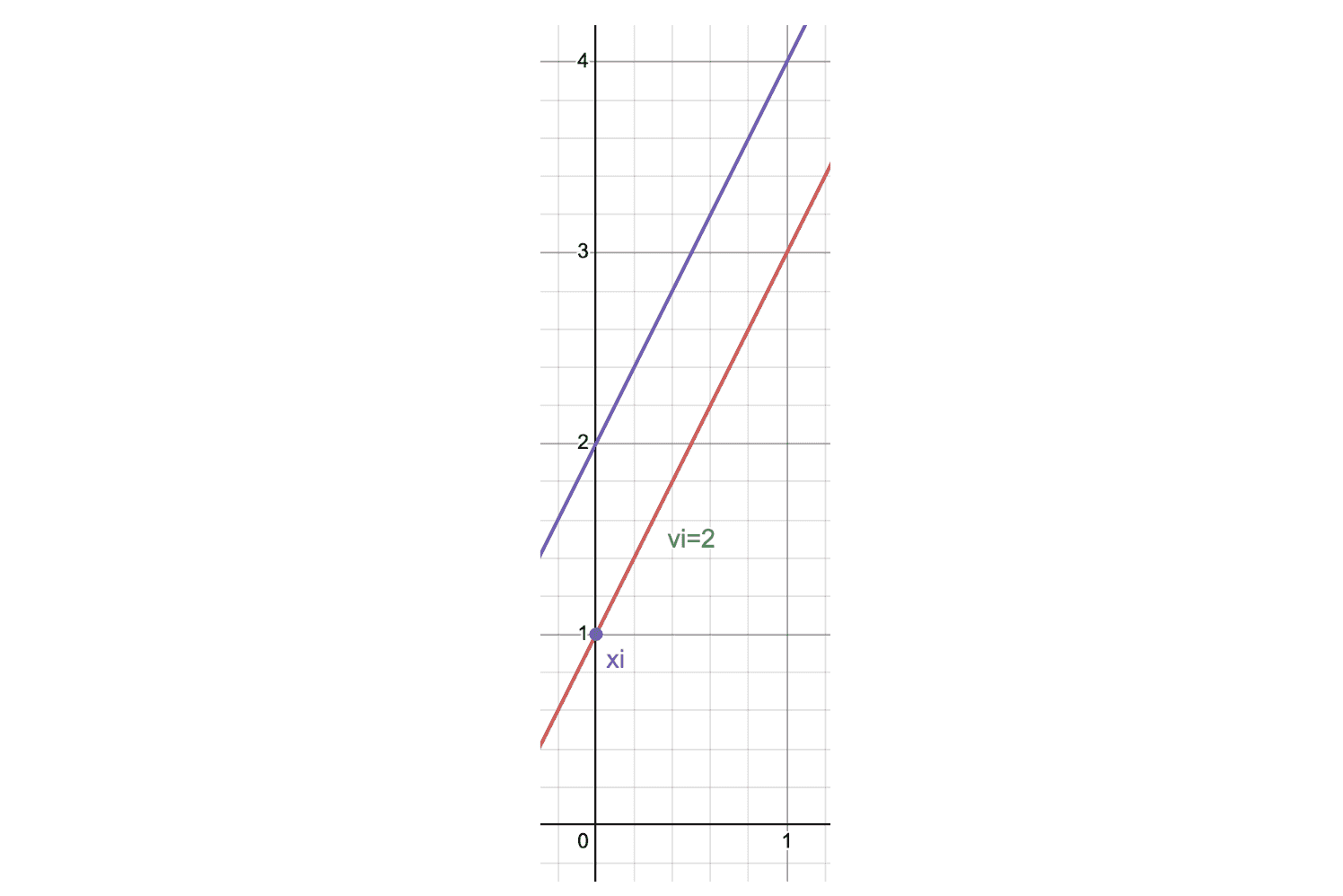
这两条线有什么用呢？我们对于其他每条鱼画出一条行动函数 \(y=v_ix+x_i\)，则这条鱼在时刻 \(t\) 能处在以 \(i\) 为左端点的区间内，当且仅当在函数的 \(t\) 位置能处在红线和蓝线之间。于是，我们可以对每个函数处理出它与红线和蓝线的交点，则在这两个交点之间的部分才可以被统计上。于是，问题转化为选择一个 \(t\)，使得在 \(t\) 位置，处在两条线之间的直线个数最多。这个问题可以通过扫描线完成，进入区域时 \(+w\)，出区域时 \(-w\)，发生变化时统计即可。单次复杂度 \(O(n)\)，总复杂度 \(O(n^2)\)。

By miao22

#include<bits/stdc++.h>
using namespace std;
bool cmp(pair<pair<int,int>,int>x,pair<pair<int,int>,int>y){
	if(x.first.first*y.first.second!=x.first.second*y.first.first)
		return x.first.first*y.first.second<x.first.second*y.first.first;
	return x.second<y.second;
}
int n,a,w[2003],x[2003],v[2003],ans;
int main(){
	cin>>n>>a;
	for(int i=0;i<n;i++)
		cin>>w[i]>>x[i]>>v[i];
	for(int i=0;i<n;i++){
		int sum=0;
		vector<pair<pair<int,int>,int> >V;
		for(int j=0;j<n;j++){
			if(v[i]==v[j])
				if(x[i]<=x[j]&&x[j]<=x[i]+a)
					sum+=w[j];
			if(v[i]<v[j]){
				V.push_back({{x[i]-x[j],v[j]-v[i]},j});
				V.push_back({{x[i]+a-x[j],v[j]-v[i]},j+n});
			}
			if(v[i]>v[j]){
				V.push_back({{x[j]-x[i]-a,v[i]-v[j]},j});
				V.push_back({{x[j]-x[i],v[i]-v[j]},j+n});
			}
		}
		sort(V.begin(),V.end(),cmp);
		int j;
		for(j=0;j<V.size();j++)
			if(V[j].first.first<0)
				if(V[j].second<n)
					sum+=w[V[j].second];
				else
					sum-=w[V[j].second-n];
			else
				break;
		ans=max(ans,sum);
		for(j;j<V.size();j++){
			if(V[j].second<n)
				sum+=w[V[j].second];
			else
				sum-=w[V[j].second-n];
			ans=max(ans,sum);
		}
	}cout<<ans;
}