ABC-282解题报告
C. String Delimiter
题意：有一个包含字母、双引号（保证有偶数个，相邻两个匹配）和逗号的字符串，将在双引号外的逗号改为句号。
维护当前在双引号里还是外，遇到双引号更改即可。
By SSRS
#include <bits/stdc++.h>
using namespace std;
int main(){
int N;
cin >> N;
string S;
cin >> S;
bool c = false;
for (int i = 0; i < N; i++){
if (S[i] == '"'){
c = !c;
}
if (S[i] == ',' && !c){
S[i] = '.';
}
}
cout << S << endl;
}
D. Make Bipartite 2
题意：给你一个无向图，判断有多少无序点对 \((x,y)\) 满足之间没有边，且连接之后为二分图。
对于一个连通块，生成二分图的方式是唯一的，且加边不会导致一个非二分图变为二分图。于是只要有一个连通块不是二分图，答案一定为 \(0\)。
对于不为 \(0\) 的情况，可以预处理每个连通块两边的点数，对于连通块内部的边，一定是左边连向右边，方案数为两边点数之积。对于连通块之间的边，任意连边都可以。在第一种情况中，有 \((x,y)\) 之间有边的情况，所以最后减去 \(m\) 即可。正确性容易证明。
By wygz
const int maxn=(2e5)+10;
int n,m,cnt[2];
int col[maxn]; vector<int> g[maxn];
ll C2(ll x) { return x*(x-1)/2; }
ll ans;
void dfs(int u) {
cnt[col[u]-1]++;
for (int &v : g[u]) {
if (col[v]&&col[v]==col[u]) { puts("0"); exit(0); }
if (col[v]) continue;
col[v]=3-col[u];
dfs(v);
}
}
int main() {
read(n),read(m);
int x,y; for (int i=1;i<=m;i++) {
read(x),read(y);
g[x].push_back(y),g[y].push_back(x);
}
for (int i=1;i<=n;i++) if (!col[i]) {
cnt[0]=cnt[1]=0;
col[i]=1,dfs(i);
ans-=C2(cnt[0]),ans-=C2(cnt[1]);
}
ans-=m;
ans+=C2(n);
printf("%lld\n",ans);
return 0;
}
还有一种维护二分图的方法，将一个点 \(i\) 拆成两个点 \(i,i'\)（实现上可以用 \(i+n\)），原图中连一条边 \(u,v\) 时，我们连接 \(u,v'\) 和 \(v,u'\)。此时维护的图中一条边 \(x,y\) 表示 \(x,y\) 异色。如下图：
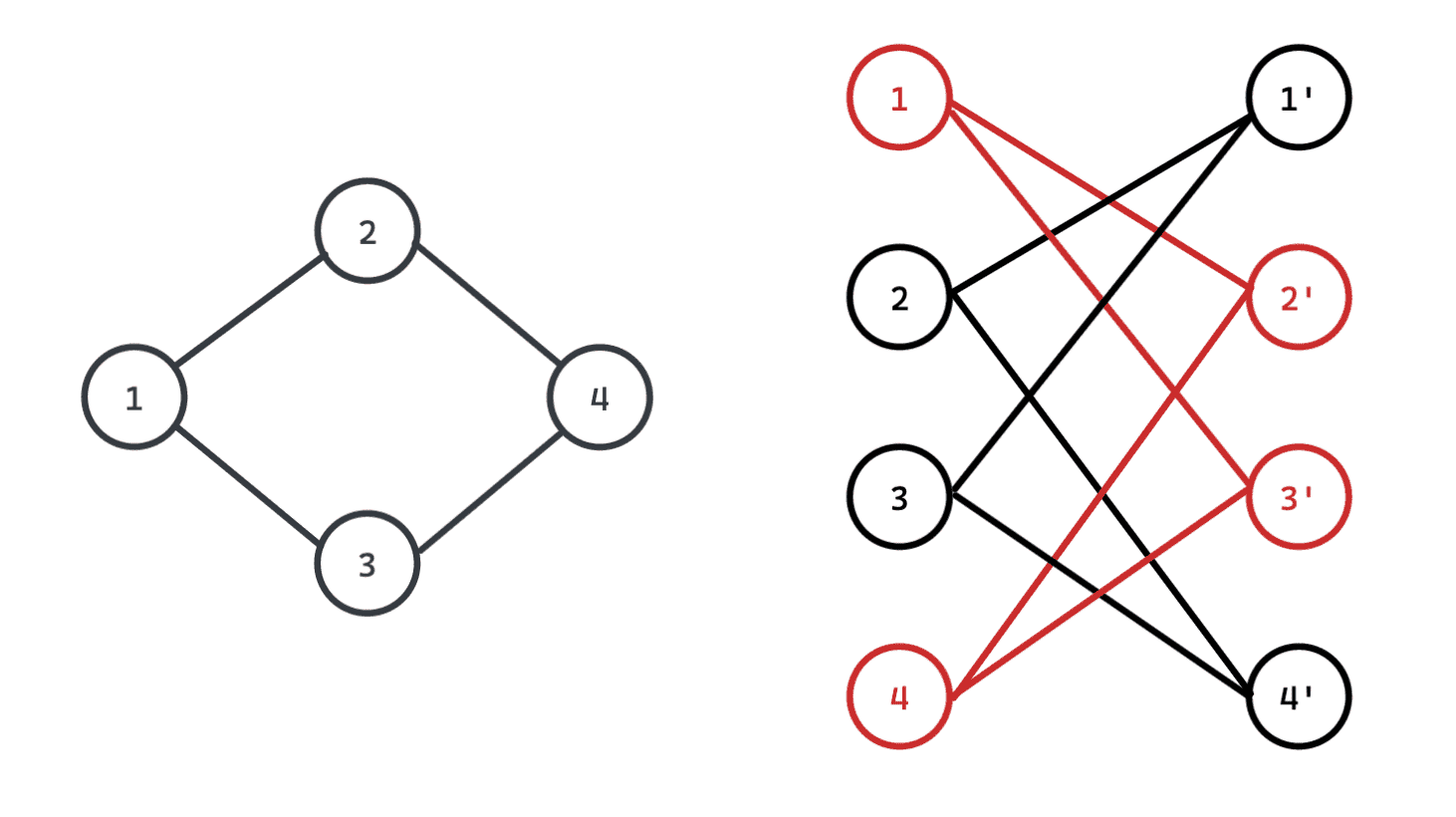
左边的图为原图，右边为维护的图。容易发现，左边的图为二分图，而右边的图可以拆成红黑两部分。左边红色的点 \(1,4\) 为原二分图中的一边，左边黑色的点 \(2,3\) 为原二分图中的另一边。
显然，如果两个点 \(u,v\) 在二分图的两侧，那么 \(u,v\) 一定不连通，\(u,v'\) 一定连通。于是有点 \(u\) 和 \(u'\) 一定不连通。
什么时候不是二分图呢？如下图，连接 \(2,3\)：
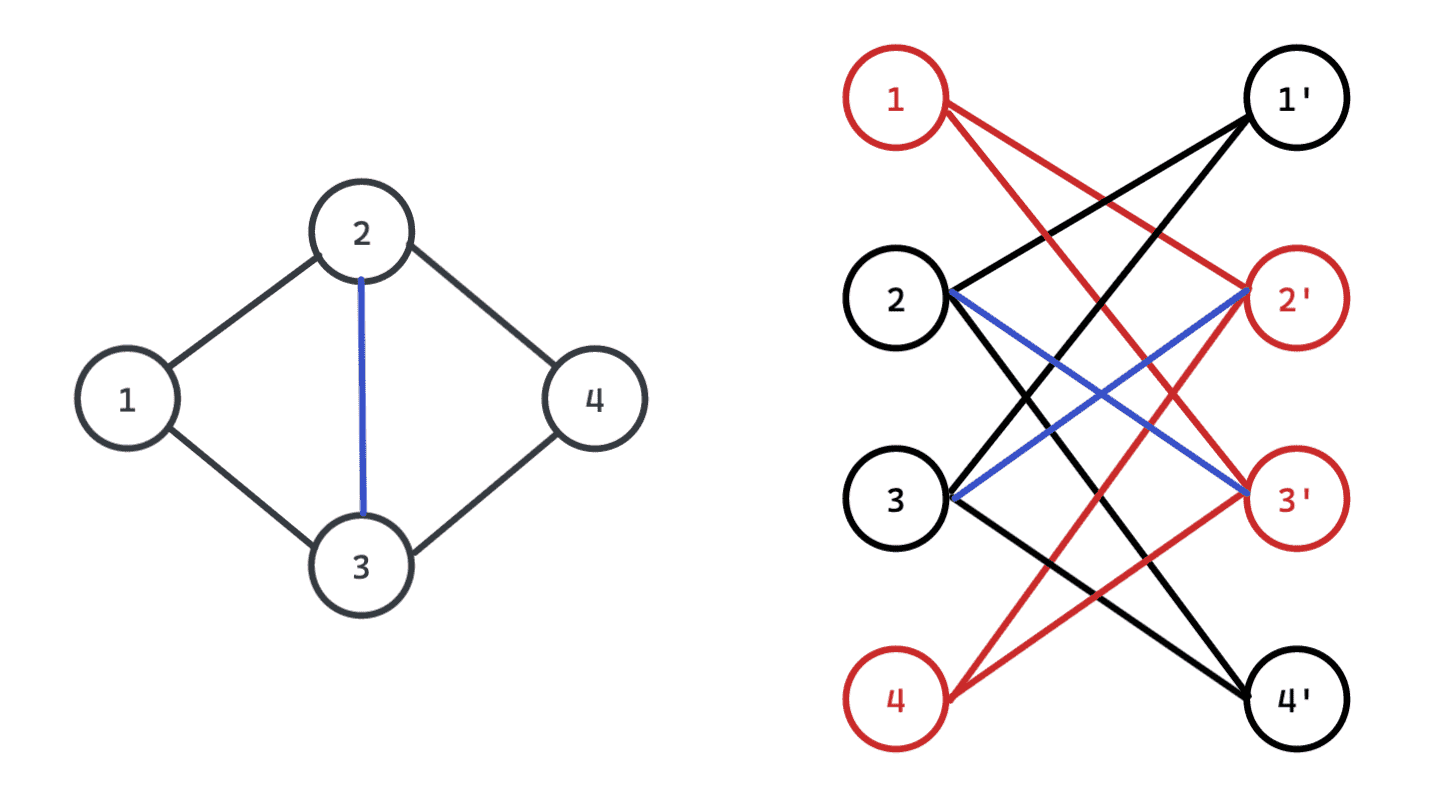
加上这条蓝色边后，可以发现维护的图合并成了一部分。此时点 \(u\) 和点 \(u'\) 变得连通，就无法产生二分图。这种二分图的表示可以很容易用并查集维护，加完边最后判断每个 \(u\) 和 \(u'\) 是否连通即可。二分图两边点的个数也可以很容易地用并查集统计（红点之间相连，黑点之间相连）。
By drogskol
#include <bits/stdc++.h>
using namespace std;
#include <atcoder/dsu>
using namespace atcoder;
using ll=long long;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
ll n,m;cin>>n>>m;
ll ans=n*(n-1)/2-m;
dsu uf(n*2);
while(m--){
int u,v;cin>>u>>v;u--;v--;
uf.merge(u,v+n);
uf.merge(v,u+n);
}
map<int,int> mp;
for(int i=0;i<n;i++){
if(uf.same(i,i+n)){
cout<<0<<endl;
return 0;
}
ans-=mp[uf.leader(i)]++;
}
cout<<ans<<endl;
}
E. Choose Two and Eat One
题意：有 \(n\) 个有权值的球，每次可以选两个球 \(a_i,a_j\)，造成 \(({a_i}^{a_j}+{a_j}^{a_i})\bmod m\) 的贡献，并选择一个球删掉。问剩一个球时的最大贡献。
由于贡献的式子没有规律，所以不能从 \(a_i\) 的角度贪心，而思考一下会发现 DP 状态也设不了，于是考虑其他思路。
我们将每个球 \(i\) 被删掉的时候与别的球 \(j\) 造成的贡献看为一条从 \(i\) 连向 \(j\) 的边，显然每个 \(i\)（除了最后一个点）有一条出边，但可能有多个入边。容易发现此为一个树形结构。而两个球的贡献同样可以在图上表示出来，为一个完全图。所以，答案即为图上最大生成树的权值。将最小生成树算法反向操作即可。
By SSRS
#include <bits/stdc++.h>
using namespace std;
long long modpow(long long x, long long y, long long M){
long long ans = 1;
while (y > 0){
if (y % 2 == 1){
ans *= x;
ans %= M;
}
x *= x;
x %= M;
y /= 2;
}
return ans;
}
struct unionfind{
vector<int> p;
unionfind(int N){
p = vector<int>(N, -1);
}
int root(int x){
if (p[x] < 0){
return x;
} else {
p[x] = root(p[x]);
return p[x];
}
}
bool same(int x, int y){
return root(x) == root(y);
}
void unite(int x, int y){
x = root(x);
y = root(y);
if (x != y){
if (p[x] < p[y]){
swap(x, y);
}
p[y] += p[x];
p[x] = y;
}
}
};
int main(){
int N, M;
cin >> N >> M;
vector<int> A(N);
for (int i = 0; i < N; i++){
cin >> A[i];
}
vector<tuple<int, int, int>> E;
for (int i = 0; i < N; i++){
for (int j = i + 1; j < N; j++){
E.push_back(make_tuple((modpow(A[i], A[j], M) + modpow(A[j], A[i], M)) % M, i, j));
}
}
sort(E.begin(), E.end(), greater<tuple<int, int, int>>());
unionfind UF(N);
long long ans = 0;
for (int i = 0; i < N * (N - 1) / 2; i++){
int c = get<0>(E[i]);
int u = get<1>(E[i]);
int v = get<2>(E[i]);
if (!UF.same(u, v)){
UF.unite(u, v);
ans += c;
}
}
cout << ans << endl;
}
