德州扑克-从入门到入土
规则简介
52 张牌（没有大小王），若干个人，进行许多轮游戏。每轮游戏过程如下：
- 初始有一个按钮（标记该轮的起点）位于某位置，顺时针方向两人依次叫“小盲”、“大盲”。首先由“小盲”和“大盲”依次下“盲注”（不可不下），这决定了这局游戏大致的格局大小。
- 由荷官发牌，每人两张，不公开。之后进行第一轮下注：顺时针依次下注，每个人可以选择与大盲下注一致，或加注至大于等于两倍大盲的金额，或者弃权。
- 由荷官公开另三张牌在中间，称为“翻牌”。之后进行第二轮下注。
- 公开第四张牌在中间，称为“转牌”。之后进行第三轮下注。
- 公开第五张牌在中间，称为“河牌”。每个玩家从自己的两张和公开的五张中确定最大的牌型组合（见下图），之后进行第四轮下注。
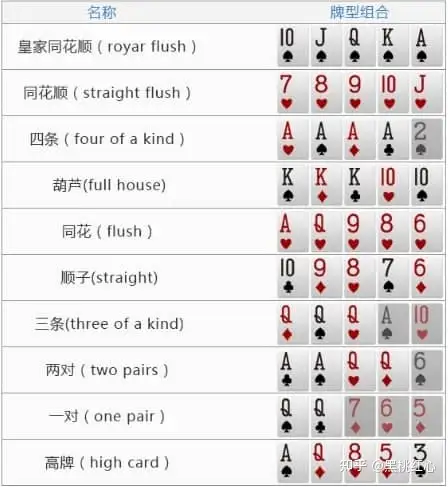
- 玩家依次摊牌，牌最大的胜出，拿走所有玩家下的注，按钮顺时针移动一格，进行下一轮。
这个游戏的奇妙之处在于，每个人不是要考虑让这一局赚的尽可能多，而是要根据按钮位置、他人策略来选择合适的策略、伪装，使若干局的总利润尽可能高。
数学模型
这里我们考虑一个基本的问题：德州扑克是纯运气游戏，还是与玩家策略有决定性关系？
由于原游戏过于复杂，这里先考虑两个人、没有盲注、注码恒为 \(1\) 的情况。设两个人分别为 A 和 B，由 A 先下注，其中 B 纯随机决定下注还是弃权，考虑 A 的策略。由于牌型的情况非常复杂，这里进一步简化：A 和 B 均获得一个 \([0,1]\) 之间的随机实数，较大的胜出。
考虑 A 取到 \(x\) 时是否应该下注。如果下注，此时，有 \(\frac{1}{2}\) 的概率 B 不下注，A 原封不动地收回 \(1\) 的注码；还有 \(\frac{1}{2}x\) 的概率 B 下注且比 A 小，此时 A 收回 \(2\) 的注码；还有 \(\frac{1}{2}(1-x)\) 的概率 B 下注且比 A 大，此时 A 收回 \(0\) 的注码。于是，若 A 取到 \(x\) 时下注，收入的期望为 \(E(x)=\frac{1}{2}\cdot 1+\frac{1}{2}x\cdot 2+\frac{1}{2}(1-x)\cdot 0=x+\frac{1}{2}\)。为了让 A 回本，我们要求期望 \(\ge 1\) 时 A 下注。解得当 \(x\ge \frac{1}{2}\) 时 A 应该下注。
若 A 采用“当 \(x\ge\frac{1}{2}\) 时下注”的策略，每局期望能净赚多少钱呢？首先考虑有多大的概率赚到 \(1\)：若 A 选到了 \(x\)（由前可知，\(x\ge \frac{1}{2}\)，否则根本不会下注），则赚到 \(1\) 的概率为 \(\frac{1}{2}x\)，所以总的赚到 \(1\) 的概率为 \(\int_\frac{1}{2}^1 \frac{1}{2}x\text{d}x=\frac{3}{16}\)。然后考虑有多大的概率亏 \(1\)：若 A 选到了 \(x\)，则亏 \(1\) 的概率为 \(\frac{1}{2}(1-x)\)，所以总的亏掉 \(1\) 的概率为 \(\int_\frac{1}{2}^1 \frac{1}{2}(1-x)\text{d}x=\frac{1}{4}-\frac{3}{16}=\frac{1}{16}\)。剩余 \(3/4\) 的概率不亏不赚。综上，每局的期望为 \(\frac{3}{16}\cdot 1+\frac{1}{16}\cdot (-1)+\frac{3}{4}\cdot 0=\frac{1}{8}\)。
有一种更简洁的算法：由于前面已经算出来了 A 抽到 \(x\) 时收入的期望 \(E(x)\)，利用期望的线性性，则可以得到每局利润的期望为 \(\int_\frac{1}{2}^1 (E(x)-1)\text{d}x=\frac{3}{8}-\frac{1}{2}=\frac{1}{8}\)。于是我们发现，有策略的操作比无策略的操作，每局期望竟然能赚 \(\frac{1}{8}\) 之多。
由于这种简化的问题无法完全反应实际的情况，所以后面我们会计算复杂一点的模型。但在此之前，先让我们考虑一个更有意思的问题：玩家的策略之间的影响。
如果 B 在对局中逐渐发现了 A 的策略，选择使用 A 的策略来进行还击，那么 A 要怎样改变策略才能仍保持优势呢？
类似的分析方式，考虑 A 取到 \(x\) 时是否应该下注。如果下注，此时有 \(\frac{1}{2}\) 的概率 B 不下注，A 原封不动地收回 \(1\) 的注码；还有 \(\frac{1}{2}(x-\frac{1}{2})/\frac{1}{2}\) 的概率 B 下注且比 A 小（因为 B 只有在 \(\ge\frac{1}{2}\) 时才会下注，所以已经保证 B 抽的数 \(\ge\frac{1}{2}\) 了），此时 A 收回 \(2\) 的注码；还有 \(\frac{1}{2}(1-x)/\frac{1}{2}\) 的概率下注且比 A 大，此时 A 收回 \(0\) 的注码。于是，若 A 取到 \(x\) 时下注，收入的期望为 \(E(x)=\frac{1}{2}\cdot 1+\frac{1}{2}(x-\frac{1}{2})/\frac{1}{2}\cdot 2+\frac{1}{2}(1-x)/\frac{1}{2}\cdot 0=2x-\frac{1}{2}\)。同样为了让 A 回本，我们要求期望 \(\ge 1\) 时 A 才下注。解得当 \(x\ge \frac{3}{4}\) 时 A 下注。
此时同上计算可得，在这种策略下，A 利润的期望为 \(\int_\frac{3}{4}^1 (E(x)-1)\text{d}x=\int_\frac{3}{4}^1 (2x-\frac{3}{2})\text{d}x=\frac{7}{16}-\frac{3}{8}=\frac{1}{16}\)。可见，当 B 采取上一局 A 的获胜策略时，在这局却又被新的策略所打败了。这个计算告诉我们，在德州扑克中需要根据对手的策略实时调整自己的策略，同时要学会隐藏自己的策略。
这引出了一个新的推论：任意一种策略，都存在一种策略能够战胜该策略，除非无论如何也不下注。这就产生了一个问题：该博弈的平衡点在“永不下注”上。如何打破这种平衡呢？这就是初始的“盲注”的作用了。强制“盲注”的存在使得平衡必须被打破，从而使这个博弈变得可玩性更高。
