园龄：5年5个月粉丝：19 关注：6

📂学习笔记

🔖字符串

2023-02-24 13:08阅读: 49评论: 0推荐: 0

SAM学习笔记

前言

前排提示：由于作者水平很菜，所以本篇文章不会讲最优性证明、复杂度证明。如有需要请自行搜索

前排提示2；本文巨无敌长，阅读并完全理解可能需要 $1 \sim 2$ 小时。但对于 SAM 这种恐怖算法来说， $2$ 小时其实并不多（毕竟我当初断断续续学了两天才理解）。

前排提示3：可能有点啰嗦，但在能忍受的情况下建议看完，会加深理解。

本篇文章的例子和插图全部来自 pecco 大佬的博客，作者也是通过那篇文章学会的 SAM。但那篇文章的思维跳跃比较快，有些理解写的也不是很完整（大佬博客通病），这篇文章可以看作那篇文章的详细版、简单版。

SAM 是干什么的

SAM，后缀自动机，顾名思义，是后缀的自动机（划掉）。可以理解为一个升级版的 trie 树，其中 trie 树内保存某字符串的所有后缀。例如，对于字符串 $s = aababc$ ，其 trie 树如下：

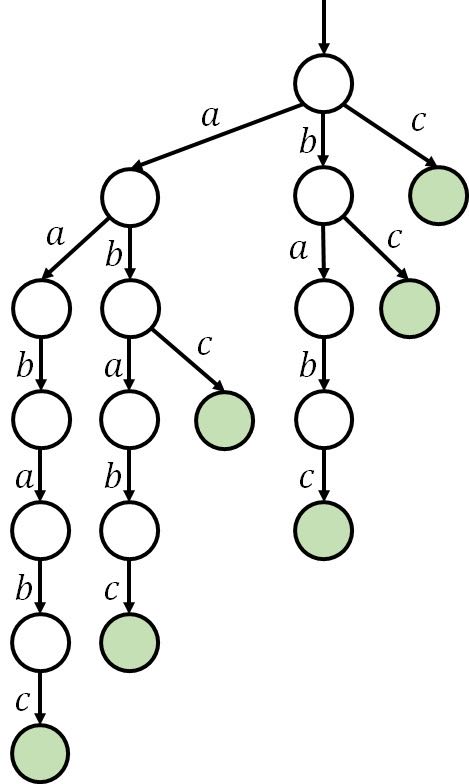
用 trie 树存字符串的每个后缀的其中一个用处为，可以快速地找到一个字符串 $t$ 是否在 $s$ 中出现（当然不止这一个用途，最后会讲应用）。

容易发现，这种 trie 树包含了很多浪费，如下图：

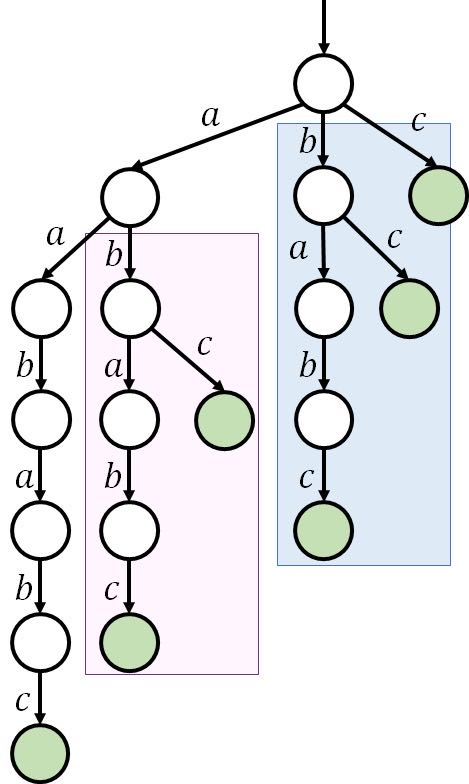
紫色的部分和蓝色的部分结构完全一样，所以可以从根节点直接连一个 $b$ 的边，指向 $ab$ 的节点。SAM 就可以理解成没有任何浪费的 trie 树。想法很自然，但如何形式化的完善这一想法呢？

endpos 集合与 parent tree

定义一个函数 $endpos (t)$ ，表示一个字符串 $t$ 在 $s$ 中所有出现的结束位置集合。如，对于上面的例子 $s = aababc$ ， $endpos (ab) = {3, 5}$ 。

另一种直观的理解方式为，我当前从字符串 $s$ 上某个位置开始走，知道我依次经过了 $t$ 的字符串，那么 $endpos (t)$ 会告诉我，当前我可能处在哪些位置。

我们发现，对于上面例子 $s = aababc$ 来说， $endpos (b) = endpos (ab) = {3, 5}$ ，那么在上面的 trie 树上， $b$ 和 $ab$ 的节点子树完全相同。感性理解，我走了 $b$ 和 $ab$ 后可能所处的位置完全相同，那么后面能怎么走自然也完全相同。

于是我们可以得出一个结论：在 SAM 中， $endpos$ 相同的字符串可以共用一个节点。形式化地，将 $s$ 的所有子串 $t$ 划分成若干个“ $endpos$ 等价类”，则每个等价类与 SAM 上的节点一一对应。

我们显然不能暴力地去找每一个等价类，这就引出了一个新概念：parent tree。它建立了所有 $endpos$ 等价类之间的关系。

还是以 $s = aababc$ 来说。如果我当前走了 $a$ ，那么我当前可能在 ${1, 2, 4}$ 。但如果我当前走了 $ba$ ，我当前只可能在 ${4}$ 。此时，在一个字符串前加上一个新的字符，可能会产生新的限制，从而将集合分裂出去。parent tree 上的边表示的就是这种分裂。

对于 $s = aababc$ ，parent tree 的形态如下：

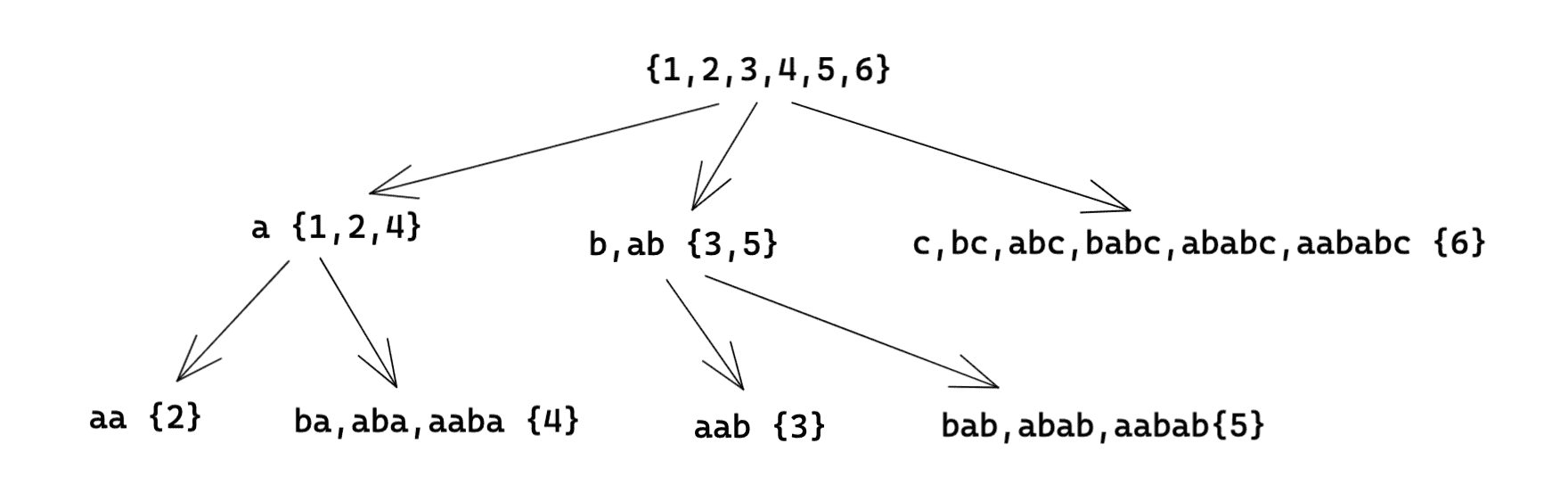
这里说一下对于这张图的感性理解：假如我走了一步，经过 $b$ ，我当前可以在 ${3, 5}$ 。如果我加强了限制，走了两步，为 $ab$ ，那么我当前仍可能在 ${3, 5}$ 。如果我走了三步，为 $bab$ ，那么我只能在 ${5}$ 。同理，如果走了四步，为 $abab$ ，同样只能在 ${5}$ 。

通过感性理解可以发现，parent tree 有几个非常重要的性质：

一个点代表的若干个字符串为最长的字符串的后缀，且长度连续（不可能出现代表 $d,bcd,abcd$ 而不代表 $cd$ 。
一个节点的祖先为该节点字符串的后缀，且依次往上遍历可以遍历到所有后缀。
由性质 2 推出，一个节点的最短字符串长度为，父亲节点的最长长度 $+ 1$ 。

接下来考虑 parent tree 的节点数（即不同的等价类个数，也就是 SAM 的节点数）。由于叶子节点的集合元素个数为 $1$ ，每个节点的元素个数都至少为儿子之和，最终根节点元素个数为 $n$ ，所以总节点数不会超过 $2 n - 1$ （易证，这里不赘述）。

构建 SAM

来到重头戏了！在这里，我们采取动态构造的方法，依次加入每个字符，并同时维护 parent tree 和 SAM。因为两者的节点一一对应，所以我们在同一个结构体里维护：

struct node {
	int fa,nxt[26],len;
} sam[MAXN*2];

其中 sam[u].fa 表示 $u$ 在 parent tree 上的父亲，sam[u].nxt[ch] 表示 $u$ 在 SAM 上经过 $c h$ 到达的节点，sam[u].len 表示 $u$ 所表示的最长字符串的长度。最短长度即为 sam[sam[u].fa].len+1。

这里先把算法流程过一遍，有一个框架，后面再详细说明。

首先有根节点，这里设为 $1$ 号节点。

加入字符的过程中，维护当前整个串对应的节点 $l s t$ 。

加入一个字符 $c h$ 时，新建一个节点 $c u r$ 表示整个串（也可能表示了其他串，但整串是最长的）。

从 $l s t$ 开始在 parent tree 上往上爬，直到爬到一个节点 $p$ 已经存在 $c h$ 的出边。在这之前，每个节点都没有 $c h$ 的出边，所以新建一个 $c h$ 的出边指向 $c u r$ 。

如果爬完了 parent tree，每个节点都没有 $c h$ 的出边，则将 sam[cur].fa 设为根。否则，设碰到的节点为 $p \overset{c h}{\to} q$ ，作如下判断：

如果 sam[p].len+1==sam[q].len，那么将 sam[cur].fa 设为 $q$ ，结束。

否则，新建一个节点 $r$ ，信息与 $q$ 完全相同，但 sam[r].len=sam[sam[q].fa].len+1，并将 sam[q].fa 和 sam[cur].fa 改为 $r$ 。接下来，让 $p$ 继续往上爬，对于每个 $p \overset{c h}{\to} q$ 改为 $p \overset{c h}{\to} r$ 。

最后将当前整个串的节点 lst 改为 cur。

int cnt=1,lst=1;
void insert(int ch) {
	int cur=++cnt,p=lst;
	sam[cur].len=sam[lst].len+1;
	for(;p&&!sam[p].nxt[ch];p=sam[p].fa)
		sam[p].nxt[ch]=cur;
	int q=sam[p].nxt[ch];
	if(!q) sam[cur].fa=1;
	else if(sam[p].len+1==sam[q].len) sam[cur].fa=q;
	else {
		int r=++cnt;
		sam[r]=sam[q],sam[r].len=sam[p].len+1;
		for(;p&&sam[p].nxt[ch]==q;p=sam[p].fa)
			sam[p].nxt[ch]=r;
		sam[q].fa=sam[cur].fa=r;
	}
	lst=cur;
}

看完肯定非常晕，但没关系，我们接下来通过一个例子，将每一步的原理解释清楚。

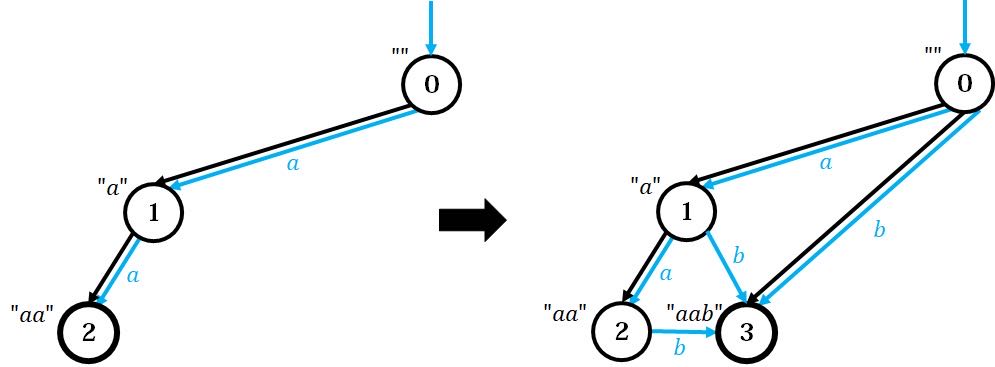
对于 $s = aababb$ ，我们模拟一遍上述过程。前面的两个字符不具有代表性，我们从第三个开始。

左图为加入前两个字符 $aa$ 后的形态，右图新加入了字符 $b$ 。观察左图，根据前面说的过程，找到原先整个串对应的节点 $2$ ，顺着黑色的 tree 边往上爬。容易发现，一直到根节点，每个节点都不存在 $b$ 的出边。于是将每个点走 $b$ 的出边连向新点 $3$ 。

我们当然不只是模拟过程，接下来进行解释：

根据 tree 的性质，在原图上往上爬一定能遍历原串所有的后缀，且是从长往短遍历。我们希望让新图也能存下新串的所有后缀，而新串的后缀等于原串后缀+字符 $b$ 。所以，如果一个原串后缀没有字符 $b$ 的出边，就说明对应的这个新串后缀没有被保存过，必须向新点连 $b$ 的边。连边的意思是，让原串后缀点+字符 $b$ 得到的新串后缀，归属这个新点。

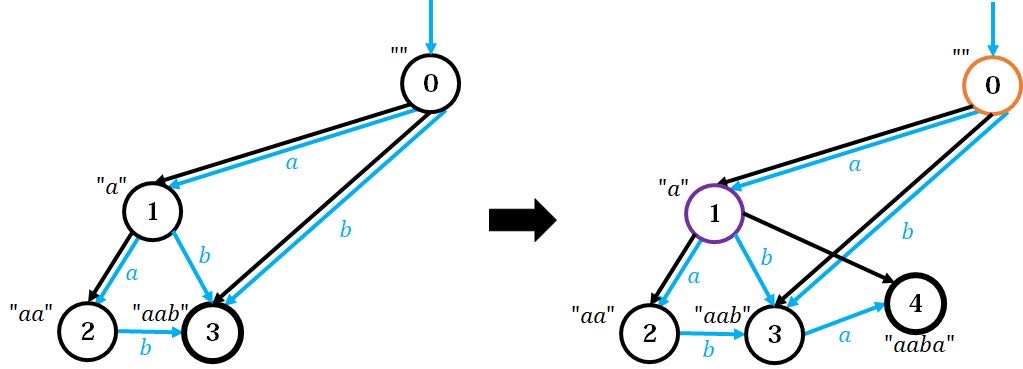
这里一直到根节点都不存在 $b$ 的出边，也就说明原串中不存在任何一个新串的后缀。然而，新节点的 fa 必须为新串的后缀，所以只能连表示空串的根节点了。

左图为加入 $aab$ 后的形态，右图为新加入字符 $a$ 后的形态。观察左图，同样模拟一开始说的过程：找到整个串对应的节点 $3$ ，没有 $a$ 的出边，所以连到新节点 $4$ ；往上爬到 $0$ ，发现 $0$ 已经有了一条 $a$ 的出边指向 $1$ ，且 $1$ 的 $l e n$ 等于 $0$ 的 $l e n + 1$ ，所以将新点 $4$ 的 fa 设为 $1$ 。

事情就是从这里开始奇怪的。这里的过程明显比上面难懂，解释如下：

考虑节点 $3$ 表示的字符串有哪些。容易发现，在原串的所有后缀中， $aab,ab,b$ 归到节点 $3$ 。由于能归到同一个节点，它们同属一个等价类，也就是对后面的影响可以看作等价的。这个节点不存在 $a$ 的出边，意味着原串不存在 $aaba,aba,ba$ ，但这些都是新串的后缀。那么我们将这个节点连到 $4$ ，就意味着让 $aaba,aba,ba$ 都归属到节点 $4$ 。但是新串的后缀不止有这三个，还有更短的 $a$ 等，于是继续往上跳。

跳到了节点 $0$ ，它表示的字符串为空串，通过字符 $a$ 的出边自然就是 $a$ 。这里已经有节点 $1$ 表示 $a$ 了，说明新串的后缀 $a$ 已经在原串中出现过，那么就不需要让 $a$ 来归属 $4$ 了，只需归属 $1$ 即可。为了让 $4$ 往上跳能跳到所有后缀，我们让它的 fa 设为 $1$ 。如果有更短的后缀，自然也在原串中出现过，从 $1$ 往上跳也能遍历到，所以不需要再添加新边了。

读到这里，可能还有一个疑问，为什么要求 $1$ 的 $l e n$ 等于 $0$ 的 $l e n + 1$ 呢？这个问题我们将在下面对比解释。

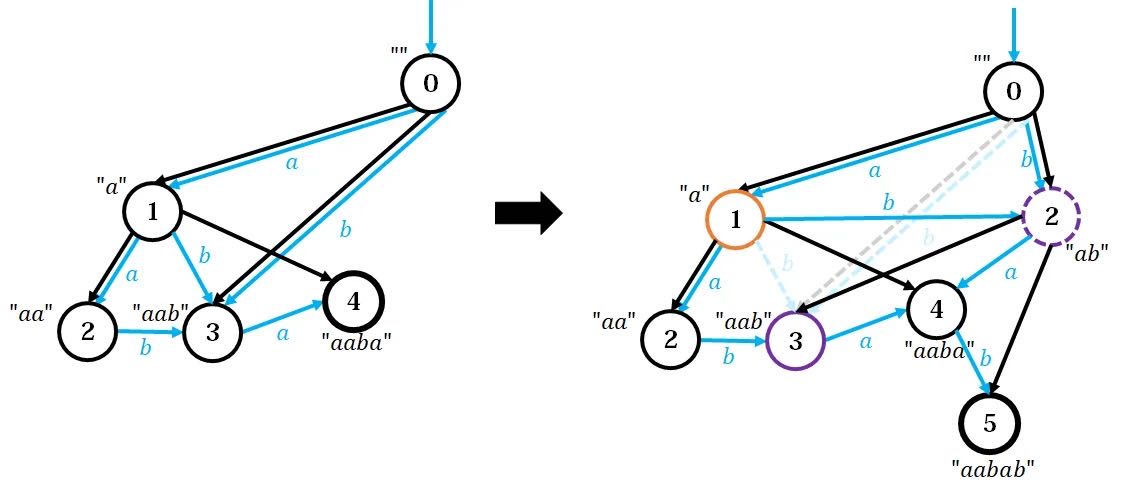
左图为添加 $aaba$ 后的形态，右图新添加了字符 $b$ 。这次我们不模拟了，直接开始讲解（因为太麻烦了）。

观察左图，找到原串的节点 $4$ ，它代表的字符串有 $aaba,aba,ba$ ，这些都是原串的后缀，而它们不存在 $b$ 的出边，即原串中不存在 $aabab,abab,bab$ ，所以要连到新点 $5$ 上。此时新点 $5$ 表示的字符串有 $aabab,abab,bab$ 。

接着沿着 tree 往上爬，找到节点 $1$ ，它代表的字符串为 $a$ 。这个节点存在 $b$ 的出边，指向 $3$ ，这意味着原串中已经存在新串的后缀 $ab$ ，且归属节点 $3$ 。

如果我们像上面一样，直接把新点 $5$ 的 fa 设为 $3$ ，即节点 $3$ 为新串的后缀，就会产生问题： $3$ 所代表的另一个字符串 $aab$ 并非新串后缀。

因为， $3$ 的 $l e n$ 并不是 $1$ 的 $l e n + 1$ ，这意味着 $3$ 代表的最长串并非由 $1$ 转移而来。如果 $3$ 表示的某个串比 $ab$ 更长，则其一定不是新串后缀。这是因为，比 $ab$ 更长的新串后缀如 $bab$ 等，已经确定在原串中没有出现，所以才连到了新点 $5$ 。

原来，在原串中 $ab$ 和 $aab$ 之所以能共用一个节点 $3$ ，是因为历史的局限性，我们以为这两个串是等价的。但加上新字符后，我们发现， $ab$ 是新串后缀而 $aab$ 不是，所以这两个必须区分开。为此，我们专门开一个新节点 $r$ ，只存这个 $ab$ ，而剥夺节点 $3$ 对 $ab$ 的占有权。

由于以前这两个等价，所以 $r$ 应该与节点 $3$ 有相同的出边，但对于所有原串的更短的后缀 $x$ ，如果 $x \overset{b}{\to} 3$ ，则更改为 $x \overset{b}{\to} r$ 。这是因为， $x$ 存的一定为 $a$ 的后缀，添加一个字符 $b$ 才到 $ab$ ，而现在 $r$ 才是真的 $ab$ ，所以要这样连。对于那些连到 $3 : aab$ 的点，如 $2 : aa$ ，一定不是原串的后缀，不会被更改。

此时，还要将 $3$ 的 fa 设为 $r$ （因为 $r$ 显然是 $3$ 的后缀），且 $r$ 的 fa 设为 $3$ 的原 fa。这样，我们才能在 tree 上正确的遍历这些串的后缀。最后的最后，别忘了将新点的 fa 设为 $r$ 。

现在可以解释第二节最后的问题了：为什么 $0$ 的 $l e n + 1$ 等于 $1$ 的 $l e n$ ，就不需要这么麻烦？因为此时 $1$ 代表的字符串总共就只有一个，不会出现因历史局限性而混淆两个串的情况，是合法的新串后缀。

完结撒花！ 如果有哪些部分没看懂或不清楚，强烈建议先对照图和算法流程模拟一遍，再看我的解析。个人认为绝对能理解（蜜汁自信）

应用

基础应用可以直接看 pecco 大佬的原文，讲得比较明白。这里着重说一下较难理解的最长公共子串。

要求 $s$ 和 $t$ 的最长公共子串，可以对 $s$ 建 SAM，从左到右扫 $t$ 的每一位，算以这一位结尾的最长公共子串所在的节点。每次新加入一位时，如果可以直接转移则转，如果没有这条转移边，就退而求其次，跳到 fa 节点试图转移（因为 fa 是本质不同的最长后缀），直到有转移边为止。

如果要求 $s_{1}, s_{2}, \dots, s_{n}$ 的最长公共子串，可以对 $s_{1}$ 建 SAM，把 $s_{2} \sim s_{n}$ 都跑一遍，对每个节点算出跑到这个节点的最短长度（因为要公共子串），最后取 $max$ 。注意，跑到一个节点相当于也跑到了它的 tree 上的祖先（因为祖先是后缀），所以要树形 DP 更新一遍再统计答案。

更多神仙应用可参见 OI-wiki。

例题

由于作者很菜，所以这里只放链接，就不班门弄斧了。

上一篇TimusOJ杂题集锦

posted @ 2023-02-24 13:08 曹轩鸣阅读(49) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

cxm1024的博客

SAM学习笔记

前言

SAM 是干什么的

endpos 集合与 parent tree

构建 SAM

应用

例题

公告

常用链接

我的标签

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论