线段树入门

【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 $k$。
求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1 x y k：将区间 $[x, y]$ 内每个数加上 $k$。
2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

样例输出 #1

11
8
20

提示

对于 $30\%$ 的数据：$n \leq 8$，$m \leq 10$。
对于 $70\%$ 的数据：$n \leq {10}^3$，$m \leq {10}^4$。
对于 $100\%$ 的数据：$1 \leq n, m \leq {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\leq {10}^{18}$。

【样例解释】

线段树模板:

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+9;
using i64 = long long;
struct tree
{
    int l;  // 左儿子
    int r;  // 右儿子
    i64 add;// 懒标记
    i64 value;// 维护的区间内的值
};
i64 arr[MAXN];
tree t[MAXN*4+2];// 记住这里要全初始化为零
void create(int x,int l,int r)
{
    t[x].l=l,t[x].r=r;
    if(l==r)
    {
       t[x].value=arr[l];// 注意这里value是递归返回的
       return ;
    }
    int mid =t[x].l+(t[x].r-t[x].l)/2;
    create(x*2,l,mid);
    create(x*2+1,mid+1,r);
    t[x].value=t[x*2].value+t[x*2+1].value;//递归返回整个区间维护的值
}
void spread(int p)
{
    if(t[p].add!=0)//存在懒标记,那么就把懒标记往下面传递
    {
        t[p*2].value+=(t[p*2].r-t[p*2].l+1)*t[p].add;
        t[p*2+1].value+=(t[p*2+1].r-t[p*2+1].l+1)*t[p].add;
        t[p*2].add+=t[p].add;// 乘二啊我擦！！！
        t[p*2+1].add+=t[p].add;
        // 标记下移，但是只移动一次,能节省时间，待需要的时候再往下移动
        t[p].add=0;
    }
}
void change(int p,int x,int y,int z)//递归返回查询结果
{
    if(x<=t[p].l&&t[p].r<=y)// 注意这个范围，这个区间要完整包含于我ask的区间
    {
        t[p].value+=(t[p].r-t[p].l+1)*z; 
        t[p].add+=z;//代表如果要查询儿子,就必须先把懒标记下移,而这里不下移动，因为本次查询不需要再向下调整了，可以把多次调整转化成一次调整，从而提高调整效率
        return ;
    }
    spread(p);//下移懒标记,这里非常关键

    int mid=(t[p].l+t[p].r)/2;
    if(x<=mid)
    {
        change(p*2,x,y,z);//change的时候x y 是选中的范围，这个是不能改的
    }
    if(y>mid)
    {
        change(p*2+1,x,y,z);
    }
    t[p].value=t[p*2].value+t[p*2+1].value;
}
i64 ask(int p,int x,int y)
{
    if(x<=t[p].l&&y>=t[p].r)return t[p].value;
    spread(p); //这里也要下传懒标记，千万别忘了，如果是查询或者修改子数组，首先要下放懒标记
    i64 ans=0;
    int mid =(t[p].l+t[p].r)/2;
    if(x<=mid)ans+=ask(p*2,x,y);//同理，ask 的时候也不能改！
    if(y>mid) ans+=ask(p*2+1,x,y);
    return ans;
}
int main()
{
    int n,m;
    std::cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        std::cin>>arr[i];
    }
    create(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int t;
        std::cin>>t;
        if(t==1)
        {
            int a,b,c;
            std::cin>>a>>b>>c;
            change(1,a,b,c);
        }
        else
        {
            int x,y;
            std::cin>>x>>y;
            i64 ans= ask(1,x,y);
            cout<<ans<<'\n';
        }
    }
    return 0;
}

这里放一下链接：

大佬的线段树讲解

【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面三种操作：

将某区间每一个数乘上 $x$；
将某区间每一个数加上 $x$；
求出某区间每一个数的和。

输入格式

第一行包含三个整数 $n,q,m$，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $q$ 行每行包含若干个整数，表示一个操作，具体如下：

操作 $1$：格式：1 x y k 含义：将区间 $[x,y]$ 内每个数乘上 $k$

操作 $2$：格式：2 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$

操作 $3$：格式：3 x y 含义：输出区间 $[x,y]$ 内每个数的和对 $m$ 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 $3$ 的结果。

样例 #1

样例输入 #1

样例输出 #1

17
2

提示

【数据范围】

对于 $30 \%$ 的数据：$n\leq 8$，$q \leq 10$。
对于 $70 \%$ 的数据：$n \leq 10^3$ , $ q \leq 10^4 $。
对于 $100\%$ 的数据：$1 \leq n \leq 10^5$，$1 \leq q \leq 10^5$。

除样例外，$m = 571373$。

（数据已经过加强 ^_）

样例说明：

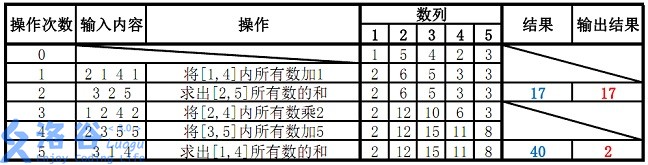
故输出应为 $17$、$2$（$40 \bmod 38 = 2$）。

AC code:

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
i64 n, q, m;
const int maxn = 1e6 + 100;

i64 ar[maxn];
struct node
{
    i64 l, r;
    i64 add;
    i64 mul;
    i64 pre;
};
node tr[maxn + 4];
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)
void create(i64 x, i64 start, i64 end)
{
    tr[x].l = start, tr[x].r = end;
    tr[x].mul = 1, tr[x].add = 0;
    if (start == end)
    {
        tr[x].pre = ar[start] % m;
        return;
    }
    i64 mid = (start + end) >> 1;
    create(ls(x), start, mid);
    create(rs(x), mid + 1, end);
    tr[x].pre = (tr[ls(x)].pre + tr[rs(x)].pre) % m;
}
void spread(i64 p)
{
    //
    if (tr[p].mul != 1)
    {
        tr[ls(p)].pre *= tr[p].mul;
        tr[ls(p)].pre %= m;
        tr[ls(p)].add *= tr[p].mul % m;
        tr[ls(p)].add %= m;
        tr[rs(p)].pre *= tr[p].mul;
        tr[rs(p)].pre %= m;
        tr[rs(p)].add *= tr[p].mul % m;
        tr[rs(p)].add %= m;
        tr[rs(p)].mul *= tr[p].mul;
        tr[rs(p)].mul %= m;
        tr[ls(p)].mul *= tr[p].mul;
        tr[ls(p)].mul %= m;
        tr[p].mul = 1;
    }
    if (tr[p].add != 0)
    {
        tr[ls(p)].pre += (tr[ls(p)].r - tr[ls(p)].l + 1) % m * tr[p].add % m;
        tr[rs(p)].pre += (tr[rs(p)].r - tr[rs(p)].l + 1) % m * tr[p].add % m;
        tr[ls(p)].add += tr[p].add;
        tr[ls(p)].add %= m;
        tr[rs(p)].add += tr[p].add;
        tr[rs(p)].add %= m;
        tr[p].add = 0;
    }
}
void add(i64 p, i64 x, i64 y, i64 z)
{
    if (x > tr[p].r || y < tr[p].l)
        return;
    if (x <= tr[p].l && tr[p].r <= y)
    {
        spread(p);
        tr[p].pre += (tr[p].r - tr[p].l + 1) % m * z % m;
        tr[p].pre %= m;
        tr[p].add += z % m;
        return;
    }
    spread(p);
    i64 mid = (tr[p].l + tr[p].r) >> 1;
    if (mid >= x)
    {
        add(ls(p), x, y, z);
    }
    if (mid < y)
    {
        add(rs(p), x, y, z);
    }
    tr[p].pre = (tr[ls(p)].pre + tr[rs(p)].pre) % m;
}
void mul(i64 p, i64 x, i64 y, i64 z)
{
    if (x > tr[p].r || y < tr[p].l)
        return;
    if (x <= tr[p].l && tr[p].r <= y)
    {
        spread(p);
        tr[p].pre = (tr[p].pre * z) % m;
        tr[p].mul = tr[p].mul * z % m;
        tr[p].mul %= m;
        return;
    }
    spread(p);
    i64 mid = (tr[p].l + tr[p].r) >> 1;
    if (mid >= x)
    {
        mul(ls(p), x, y, z);
    }
    if (mid < y)
    {
        mul(rs(p), x, y, z);
    }
    tr[p].pre = (tr[ls(p)].pre + tr[rs(p)].pre) % m;
}
i64 ask(i64 p, i64 x, i64 y)
{
    if (x > tr[p].r || y < tr[p].l)
        return 0;
    if (tr[p].l >= x && tr[p].r <= y)
    {
        return tr[p].pre;
    }
    i64 mid = (tr[p].l + tr[p].r) >> 1;
    i64 ans = 0;
    spread(p);
    if (mid >= x)
    {
        ans += ask(ls(p), x, y);
        ans %= m;
    }
    if (mid < y)
    {
        ans += ask(rs(p), x, y);
        ans %= m;
    }
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(0);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> n >> q >> m;
    for (int i = 1; i <= n; i++)
        std::cin >> ar[i];
    create(1, 1, n);
    for (int i = 1; i <= q; i++)
    {
        int t;
        std::cin >> t;
        i64 x, y, k;
        switch (t)
        {
        case 1:
            std::cin >> x >> y >> k;
            // mul
            mul(1, x, y, k);
            break;
        case 2:
            std::cin >> x >> y >> k;
            // add
            add(1, x, y, k);
            break;
        case 3:
            std::cin >> x >> y;
            i64 ans = ask(1, x, y);
            std::cout << ans << '\n';
            break;
        }
    }
    return 0;
}

这一题的关键就是对于两个$lazytag$的优先级的转换，然后就是普通的线段树的修改，但是我的代码因为对线段树不熟悉，包含一些多余的步骤，耗时比较多，还有很多细节可以优化。

[JSOI2008] 最大数

题目描述

现在请求你维护一个数列，要求提供以下两种操作：

查询操作。

语法：Q L

功能：查询当前数列中末尾 $L$ 个数中的最大的数，并输出这个数的值。

限制：$L$ 不超过当前数列的长度。$(L > 0)$

插入操作。

语法：A n

功能：将 $n$ 加上 $t$，其中 $t$ 是最近一次查询操作的答案（如果还未执行过查询操作，则 $t=0$），并将所得结果对一个固定的常数 $D$ 取模，将所得答案插入到数列的末尾。

限制：$n$ 是整数（可能为负数）并且在长整范围内。

注意：初始时数列是空的，没有一个数。

输入格式

第一行两个整数，$M$ 和 $D$，其中 $M$ 表示操作的个数，$D$ 如上文中所述。

接下来的 $M$ 行，每行一个字符串，描述一个具体的操作。语法如上文所述。

输出格式

对于每一个查询操作，你应该按照顺序依次输出结果，每个结果占一行。

样例 #1

样例输入 #1

样例输出 #1

96
93
96

提示

数据规模与约定

对于全部的测试点，保证 $1 \leq M \leq 2 \times 10^5$，$1 \leq D \leq 2 \times 10^9$。

其实用ST表也可以写，而且时间复杂度更低，但是我现在是在联系线段树，所以就再练了一手线树维护最值的代码

AC code:

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
i64 M, D;
const int maxn = 2e5 + 9;
i64 ar[maxn],num;
struct tree
{
    int l, r;
    i64 pre;
};
tree t[4 * maxn];
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)

void create(int p, int l, int r)
{
    t[p].l = l, t[p].r = r;
    if (l == r)
    {
        t[p].pre = ar[l];
        return;
    }
    int mid = (l + r) >> 1;
    create(ls(p), l, mid);
    create(rs(p), mid + 1, r);
    t[p].pre = std::max(t[ls(p)].pre , t[rs(p)].pre);
}
void change(int p, int x,i64 z)
{
    if (t[p].l > x || t[p].r < x)
        return;
    if (t[p].l == t[p].r)
    {
        // t[p].tag=true; 查询最值的时候不需要懒标记
        t[p].pre = z;
        return ;
    }
    int mid = (t[p].l + t[p].r) >> 1;
    if (mid >= x)
        change(ls(p), x,z);
    if (mid < x)
        change(rs(p), x,z);
    t[p].pre = std::max(t[ls(p)].pre, t[rs(p)].pre);// 这里存在越界的可能！！！！
}
i64 search(int p, int x, int y)
{
    if (t[p].r < x || t[p].l > y)
        return LONG_LONG_MIN;
    if (x <= t[p].l && t[p].r <= y)
    {
        return t[p].pre;
    }
    i64 ans = LONG_LONG_MIN;
    int mid = (t[p].l + t[p].r) >> 1;
    if (mid >= x)
        ans = std::max(ans, search(ls(p), x, y));
    if (mid < y)
        ans = std::max(ans, search(rs(p), x, y));
    return ans;
}
int main()
{
    std::cin >> M >> D;
    int cnt = 0;
    for (int i = 1; i < maxn; i++)
        ar[i] = LONG_LONG_MIN;
    create(1,1,maxn-1);
    for (int i = 1; i <= M; i++)
    {
        char c;
        i64 x;
        std::cin>>c>>x;
        if (c == 'A')
        {
            change(1,++cnt,(x+num)%D);
        }
        else
        {
            std::cout<<(num=search(1,cnt-x+1,cnt))<<'\n';
        }
    }
    return 0;
}

无聊的数列

题目背景

无聊的 YYB 总喜欢搞出一些正常人无法搞出的东西。有一天，无聊的 YYB 想出了一道无聊的题：无聊的数列。。。

题目描述

维护一个数列 $a_i$，支持两种操作：

1 l r K D：给出一个长度等于 $r-l+1$ 的等差数列，首项为 $K$，公差为 $D$，并将它对应加到 $[l,r]$ 范围中的每一个数上。即：令 $a_l=a_l+K,a_{l+1}=a_{l+1}+K+D\ldots a_r=a_r+K+(r-l) \times D$。
2 p：询问序列的第 $p$ 个数的值 $a_p$。

输入格式

第一行两个整数数 $n,m$ 表示数列长度和操作个数。

第二行 $n$ 个整数，第 $i$ 个数表示 $a_i$。

接下来的 $m$ 行，每行先输入一个整数 $opt$。

若 $opt=1$ 则再输入四个整数 $l\ r\ K\ D$；

若 $opt=2$ 则再输入一个整数 $p$。

输出格式

对于每个询问，一行一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

对于 $100\%$ 数据，$0\le n,m \le 10^5,-200\le a_i,K,D\le 200, 1 \leq l \leq r \leq n, 1 \leq p \leq n$。

注意这题推差分数组变换要仔细一点~~就差一点就可以直接一发AC了呜呜呜~~

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int maxn = 1e5 + 9;
#define int long long
struct tree
{
    int l, r;
    i64 add;
    i64 pre;
};
tree t[maxn * 4];
i64 a[maxn], b[maxn];
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
void create(int p, int l, int r)
{
    t[p].l = l, t[p].r = r;
    if (l == r)
    {
        t[p].pre = b[l];
        return;
    }
    int mid = (l + r) >> 1;
    create(ls(p), l, mid);
    create(rs(p), mid + 1, r);
    t[p].pre = t[ls(p)].pre + t[rs(p)].pre;
}
void push_down(int p)
{
    if (t[p].add)
    {
        auto deal = [&](int x)
        {
            t[x].pre += (t[x].r - t[x].l + 1) * t[p].add;
            t[x].add += t[p].add;
        };
        deal(ls(p));
        deal(rs(p));
        t[p].add = 0;
    }
}
void change(int p, int x, int y, i64 z)
{
    if (t[p].r < x || t[p].l > y)
        return;
    if (x <= t[p].l && t[p].r <= y)
    {
        t[p].pre += (t[p].r - t[p].l + 1) * z;
        t[p].add += z;
        return;
    }
    push_down(p);
    int mid = (t[p].r + t[p].l) >> 1;
    if (mid >= x)
        change(ls(p), x, y, z);
    if (mid < y)
        change(rs(p), x, y, z);
    t[p].pre = t[ls(p)].pre + t[rs(p)].pre;
}
i64 __search(int p, int x, int y)
{
    if (t[p].r < x || t[p].l > y)
        return 0;
    if (x <= t[p].l && t[p].r <= y)
        return t[p].pre;
    push_down(p);
    int mid = (t[p].l + t[p].r) >> 1;
    i64 ans = 0;
    if (mid >= x)
        ans += __search(ls(p), x, y);
    if (mid < y)
        ans += __search(rs(p), x, y);
    return ans;
}
signed main()
{
    std::ios::sync_with_stdio(0);
    std::cin.tie(0), cout.tie(0);
    int n, m;
    std::cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        b[i] = a[i] - a[i - 1]; // 差分数组
    }
    create(1, 1, n);
    int x;
    for (int i = 1; i <= m; i++)
    {
        std::cin >> x;
        if (x == 1)
        {
            int l, r, K, D;
            cin >> l >> r >> K >> D;
            // 维护b数组
            change(1, l + 1, r, D);
            change(1, l, l, K);
            change(1, r + 1, r + 1, -K-D*(r-l));
        }
        else
        {
            std::cin >> x;
            // 求b数组的前缀和
            cout << __search(1, 1, x) << '\n';
        }
    }
    return 0;
}
/*
6
6
0 0 0 0 0 0
1 1 6 1 1
2 2
2 3
2 4
2 5
2 6

*/

posted @ 2024-07-24 19:33 -风间琉璃- 阅读(6) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

cxjy0322

线段树入门

【模板】线段树 1

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

线段树模板:

这里放一下链接：

大佬的线段树讲解

【模板】线段树 2

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

AC code:

[JSOI2008] 最大数

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

AC code:

无聊的数列

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

公告