HDU 1045 Fire Net（搜索剪枝）

http://acm.split.hdu.edu.cn/showproblem.php?pid=1045

http://acm.hdu.edu.cn/showproblem.php?pid=1045

题目链接（总有一个可以点开）……

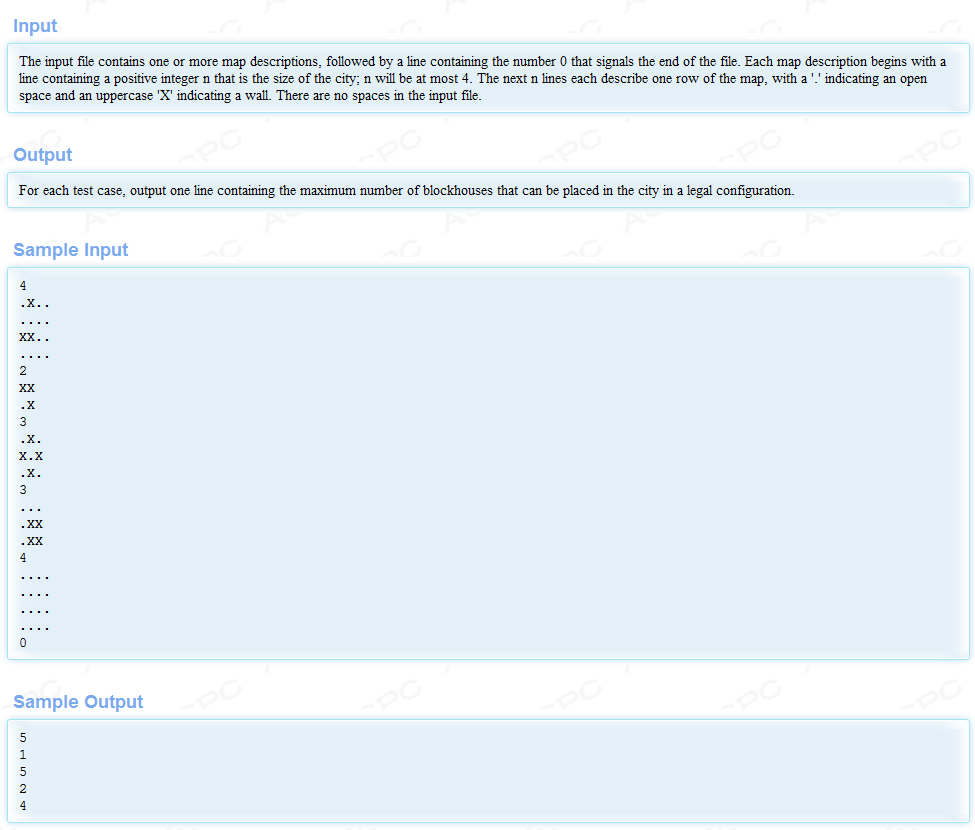
题意：给出一张地图，上面只有两种字符（.和X），X相当于无法穿透的墙。问这张地图上最多可以放置多少个互不攻击的子弹……

第一反应是搜索，然而后来看到网上有些大神说这是二分图匹配……看来还是要研究下。

我剪枝的思路：对每个点设置所有关联的点（上下左右四个方向直到被墙挡住），每个点依次存放关联点。这样每次搜索的时候就可以省一些时间，同时降低编程复杂度。

每次搜到的子弹数都用ans[]存下（ans[i]true意为可能存在大于i的可行方案），操作的时候二维表变成一位表（这样方便）。

例如有张4*4的表：

（0,0）->（0）

（0,1）->（1）

...

（1,0）->（4）

...

（3,3）->（15）

具体就是这样。

代码如下：

 1 #include <cstdio>
 2 #include <vector>
 3 #include <cstring>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <functional>
 7 
 8 using namespace std;
 9 
10 #define REP(i,n)        for(int i(0); i <  (n); ++i)
11 #define rep(i,a,b)        for(int i(a); i <= (b); ++i)
12 #define dec(i,a,b)        for(int i(a); i >= (b); --i)
13 #define for_edge(i,x)        for(int i = H[x]; i; i = X[i])
14 
15 #define LL    long long
16 #define ULL    unsigned long long
17 #define MP    make_pair
18 #define PB    push_back
19 #define FI    first
20 #define SE    second
21 #define INF    1 << 30
22 
23 const int N    =    100000        +    10;
24 const int M    =    10000        +    10;
25 const int Q    =    100        +    10;
26 const int A    =    6        +    1;
27 
28 vector <int> v[Q];
29 int c[A][A], h[A][A];
30 char st[Q];
31 bool f[Q], ans[Q];
32 int n, num, ret;
33 
34 void dfs(int k, int low, bool * f){
35     ans[k] = true; bool now = true; REP(i, n * n) if (!f[i]) { now = false; break; } if (now) return; int d[Q];
36     REP(j, num) d[j] = f[j]; rep(i, low, num - 1) if (!f[i]){ f[i] = true; REP(j, v[i].size()) f[v[i][j]] = true; dfs(k + 1, low + 1, f); REP(j, num) f[j] = d[j];}
37 }
38 
39 
40 int main(){
41 #ifndef ONLINE_JUDGE
42     freopen("test.txt", "r", stdin);
43     freopen("test.out", "w", stdout);
44 #endif
45 
46     while (~scanf("%d", &n), n){
47         REP(i, n){ scanf("%s", st); REP(j, n) c[i][j] = st[j] == '.' ? 0 : 1; }
48         //REP(i, n){ REP(j, n) putchar(c[i][j] + 48); putchar(10);}
49         int cnt = 0; REP(i, n) REP(j, n) h[i][j] = cnt++; 
50         REP(i, n * n + 10) v[i].clear(); num = n * n;
51         REP(i, n) REP(j, n) if (!c[i][j]){
52             rep(k, j + 1, n - 1){ if (c[i][k]) break; v[h[i][j]].PB(h[i][k]); }
53             rep(k, i + 1, n - 1){ if (c[k][j]) break; v[h[i][j]].PB(h[k][j]); }
54             dec(k, j - 1, 0){ if (c[i][k]) break; v[h[i][j]].PB(h[i][k]); }
55             dec(k, i - 1, 0){ if (c[k][j]) break; v[h[i][j]].PB(h[k][j]); }
56         }
57         //REP(i, n) REP(j, n){ printf("%d %d: ", i, j); REP(k, v[h[i][j]].size()) printf("%d ", v[h[i][j]][k]); puts("");} puts("");
58         memset(ans, false, sizeof ans); REP(i, n) REP(j, n) f[h[i][j]] = c[i][j];
59         REP(i, n) REP(j, n) if (!c[i][j]) dfs(0, h[i][j], f);
60         ret = 0; dec(i, num, 0) if (ans[i]){  ret = i;  break;}
61         printf("%d\n", ret);
62     }
63     
64     
65     return 0;
66     
67 }
View Code

HDU上 0MS..手动胜利！！(数据好像蛮弱的)

posted @ 2016-09-03 16:25  cxhscst2  阅读(477)  评论(1)  编辑  收藏  举报