P2862

P2862 题解

---

写数据结构的时候碰到的，最后发现和 ds 没啥关系。

数据范围很小，可以接受大约 \(O(n^2\cdot \log n)\) 的复杂度。

以下 \(v\) 表示值域（本题为 \(10^4\))。

先考虑暴力枚举正方形位置。

那么需要枚举左上角顶点位置和边长，\(O(v^3)\)；判断合法性可以二维前缀和，\(O(1)\) 查询，判断三叶草数量是否大于等于 \(C\)。

故复杂度 \(O(v^3)\)，考虑优化。

暴力的主要复杂度来源有两个：

1. 枚举顶点

2. 枚举边长

---

真的有必要枚举值域内所有点吗？有哪些点不可能作为答案？

将 有三叶草的行列 涂成灰色。

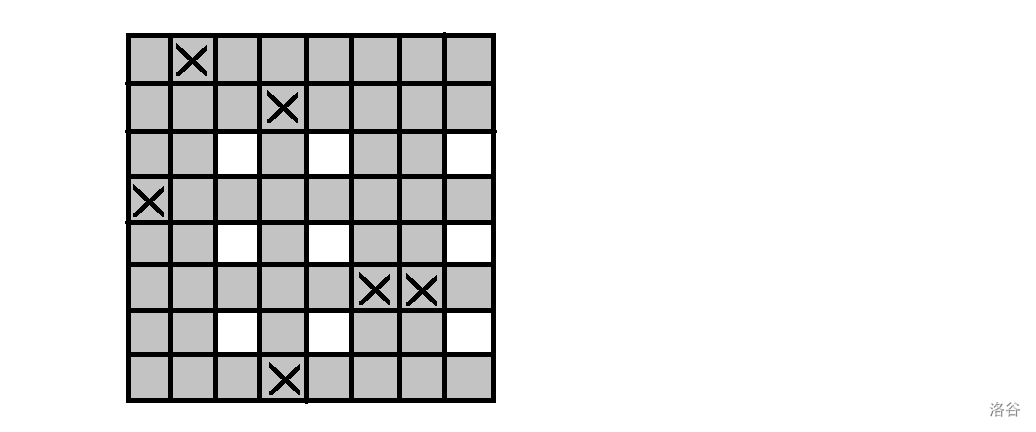
只有灰色部分可能作为正方形左上角。

如果（正方形顶点）取在白色部分，必然不优于取在它右下方。因为向右下移动 不会减少三叶草数量，但 更省边长。

所以，离散化再枚举，复杂度 \(O(v^2)\to O(n^2)\)。

---

考虑边长枚举的优化。

发现单调性：顶点枚举了，是固定的，那么正方形中的三叶草数量随边长增加而不减。可以二分。

\(O(v)\to O(\log v\cdot \log n)\)

（这个 \(\log n\) 是实现的时候带的，蒟蒻不知道怎么优化掉，但是能过qwq）

---

时间复杂度 \(O(n^2\cdot \log n\cdot \log v)\)，空间复杂度 \(O(n^2)\)。

时空复杂度带常数 \(4\)。

那么就剩下代码了。

//Problem: P2862
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define i32 INT_MAX
#define i64 LONG_LONG_MAX
#define pii pair<int, int>
#define pll pair<long long, long long>
#define pb push_back
typedef long long ll;
const int N = 1010;
ll read(){ll x=0,f=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}return x*f;}
void print(ll x){if(x<0)putchar('-'),x=-x;if(x>9)print(x/10);putchar(x%10+48);}
char gc(){char c=getchar();while(c==' '||c=='\n')c=getchar();return c;}

int n, m, c, xmax, ymax, answer = inf, l, r, mid, ans;
int x[N], y[N];
int b[N];
int map[N][N], s[N][N];

int sum(int x1, int y1, int x2, int y2) {
    return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}
// 查询：左上角 (x1, y1)，右下角 (x2, y2) 正方形中三叶草数

int main() {
    std::cin >> c >> n;
    for(int i = 1; i <= n; i++) {
        x[i] = b[++m] = read();
        y[i] = b[++m] = read();
        xmax = std::max(xmax, x[i]);
        ymax = std::max(ymax, y[i]); // 记录这个是为了判越界~
    }
    std::sort(b + 1, b + m + 1); m = std::unique(b + 1, b + m + 1) - b - 1;
    for(int i = 1; i <= n; i++) {
        x[i] = std::lower_bound(b + 1, b + m + 1, x[i]) - b;
        y[i] = std::lower_bound(b + 1, b + m + 1, y[i]) - b;
        map[x[i]][y[i]]++; // map是四叶草数量数组
    } // 离散化
    for(int i = 1; i <= m; i++)
        for(int j = 1; j <= m; j++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + map[i][j];
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= m; j++) {
            int cx = b[i], cy = b[j]; // 正方形左上角为原图中的 (cx, cy); 离散坐标 (i, j)
            if(cx > xmax || cy > ymax) continue;
            l = 0, r = std::max(xmax - cx , ymax - cy) + 1, mid, ans = inf; // 二分正方形的边长为多少原图长度
            while(l <= r) { // 二分边长
                mid = l + r >> 1;
                if(sum(i, j, std::upper_bound(b + 1, b + m + 1, cx + mid) - b - 1, std::upper_bound(b + 1, b + m + 1, cy + mid) - b - 1) >= c) {
                // upper_bound 搜索：原坐标 对应的 离散后坐标
                    r = mid - 1;
                    ans = mid;
                } else {
                    l = mid + 1;
                }
            }
            answer = std::min(answer, ans);
        }
    }
    std::cout << answer << '\n';
    return 0;
}