CSP模拟28
考废了,无语
[CF1681E] Labyrinth Adventures
有点神奇的题;
首先可以想到简单dp ,设 $dp_{i,0|1} $ 表示在第 \(i\) 层,从上 or 右门出的最短路径,
显然:
$$ dp_{i,0}= \min(dp_{i-1,0}+dis_{0,0} , dp_{i-1,1}+dis_{1,0}) $$
$$ dp_{i,1}= \min(dp_{i-1,0}+dis_{0,1} , dp_{i-1,1}+dis_{1,1}) $$
考虑优化,发现每次询问会有重复的部分,这个状态转移方程可以写成矩阵的形式,所以我们考虑用线段树维护矩阵的区间乘积,就可以过了。
复杂度 \(O(m\log n)\)
点击查看代码
#include <iostream>
#include <cstdio>
#include <cmath>
const int MAXN=1e5+10;
const int inf=2147483647;
using namespace std;
inline int read() {
int f=1,x=0;
char ch=getchar();
while(ch>'9' || ch<'0') {
if(ch=='-') {
f=-1;
}
ch=getchar();
}
while(ch>='0' && ch<='9') {
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return f*x;
}
int n,m;
struct Door {
int x1,y1;
int x2,y2;
}a[MAXN];
struct Pos {
int x,y,pos;
}s,t;
int dp[MAXN][2];
int main() {
n=read();
for(int i=1;i<n;i++) {
a[i].x1=read();
a[i].y1=read();
a[i].x2=read();
a[i].y2=read();
}
m=read();
while(m--) {
s.x=read(),s.y=read() ,t.x=read(),t.y=read();
s.pos=max(s.x,s.y) ,t.pos=max(t.x,t.y);
if(s.pos>t.pos) {
swap(s,t);
}
if(s.pos==t.pos) {
cout<<abs(s.x-t.x)+abs(s.y-t.y);
putchar('\n');
continue;
}
for(int i=1;i<=n;i++) {
dp[i][0]=dp[i][1]=inf;
}
dp[s.pos][0]=abs(a[s.pos].x1+1-s.x)+abs(a[s.pos].y1-s.y);
dp[s.pos][1]=abs(a[s.pos].x2-s.x)+abs(a[s.pos].y2+1-s.y);
for(int i=s.pos+1;i<=t.pos-1;i++) {
dp[i][0]=min(dp[i-1][0]+abs(a[i].x1-a[i-1].x1)+abs(a[i].y1-a[i-1].y1),
dp[i-1][1]+abs(a[i].x1+1-a[i-1].x2)+abs(a[i-1].y2+1-a[i].y1));
dp[i][1]=min(dp[i-1][0]+abs(a[i].y2+1-a[i-1].y1)+abs(a[i-1].x1+1-a[i].x2),
dp[i-1][1]+abs(a[i-1].x2-a[i].x2)+abs(a[i-1].y2-a[i].y2));
}
int l=dp[t.pos-1][0],r=dp[t.pos-1][1];
int ans=inf;
ans=min(l+abs(a[t.pos-1].x1+1-t.x)+abs(a[t.pos-1].y1-t.y),
r+abs(a[t.pos-1].x2-t.x)+abs(a[t.pos-1].y2+1-t.y));
cout<<ans; putchar('\n');
}
return 0;
}
[BJOI2019] 光线
考虑Dp,对于第 \(i\) 块玻璃,我们设 \(f_i\) 表示在 \(i\) 块和第 \(i+1\) 块玻璃中间方向下的光线 ,\(g_i\) 表示表示在 \(i\) 块和第 \(i-1\) 块玻璃中间方向上的光线。
光线可由穿透和反射得到,所以可以得出状态转移方程:
$$ f_i=f_{i-1}·a_i + g_{i+1}·b_i $$
$$ g_i=f_{i-1}·b_i + g_{i+1}·a_i $$
发现这个式子没办法转移,而我们最后只想要 \(f_n\) ,所以我们考虑把 \(g_{i+1}\) 消去。
而且我们知道 \(f_1=1\) ,所以可以想办法从他转移过来。
我们设 \(F_i=\frac{f_i}{f_{i-1}}\) ,$G_i=\frac{g_i}{f_{i-1}} $ ,
答案 \(ans= \prod_{i=1}^n F_i\)
考虑对式子进行操作:
$$ f_i=f_{i-1}·a_i + g_{i+1}·b_i $$
$$ \frac{f_1}{f_{i-1}}=a_i+ \frac{g_{i+1}}{f_{i-1}}·b_i $$
$$ F_i=a_i+G_{i+1}·F_i·b_i$$
$$ F_i=\frac{a_i}{1-G_{i+1}·b_i}$$
同理:
$$G_i=b_i+a_i·F_i·G_{i+1}$$
就可以递推了。
复杂度 \(O(n)\)
点击查看代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>
#define int long long
const int mod=1e9+7;
const int MAXN=5e5+10;
using namespace std;
inline int read() {
int f=1,x=0;
char ch=getchar();
while(ch>'9' || ch<'0') {
if(ch=='-') {
f=-1;
}
ch=getchar();
}
while(ch>='0' && ch<='9') {
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return f*x;
}
int n,invv;
int a[MAXN],b[MAXN];
int f[MAXN],g[MAXN];
int fpow(int x,int k) {
int res=1;
while(k) {
if(k&1) res=res*x%mod;
x=x*x%mod;
k>>=1;
}
return res;
}
int inv(int x) {
return fpow(x,mod-2)%mod;
}
signed main() {
n=read();
invv=inv(100);
for(int i=1;i<=n;i++) {
a[i]=read()*invv%mod ,b[i]=read()*invv%mod;
}
for(int i=n;i>=1;i--) {
f[i]=1ll*a[i]*inv(1ll-b[i]*g[i+1]%mod+mod)%mod;
g[i]=(b[i]+1ll*a[i]*f[i]%mod*g[i+1]%mod)%mod;
}
for(int i=2;i<=n;i++) {
f[i]=f[i]*f[i-1]%mod;
}
cout<<f[n];
return 0;
}
kkk
我不会数数
计数且不会,首先把所有数排序。对于一种合法的队列,设 \(a_i\) 为排完序后的数列,\(b_i\) 表示在第 \(i\) 位填的数,那么要有 $ b_i \geqslant a_i$ ,不然的话会被覆盖掉,没有办法产生影响。
所以设 \(dp_{i,j}\) 表示现在填了 \(i\) 个数,第 \(i\) 个数为 \(j\) .从每一个存在的比 \(j\) 的数转移。
$$ dp_{i,j}= \sum_{k=1}^{j}dp_{i,k} $$
可以前缀和优化,复杂度 \(O(n^2)\)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
const int MAXN=3010;
const int mod=1e9+7;
using namespace std;
inline int read() {
int f=1,x=0;
char ch=getchar();
while(ch>'9' || ch<'0') {
if(ch=='-') {
f=-1;
}
ch=getchar();
}
while(ch>='0' && ch<='9') {
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return f*x;
}
int n,tot;
int a[MAXN];
int dp[MAXN][MAXN];
bool vis[MAXN];
int main() {
n=read();
for(int i=1;i<=n;i++) {
a[i]=read();
vis[a[i]]=1;
dp[0][a[i]]=1;
}
sort(a+1,a+n+1);
dp[0][0]=1;
for(int i=1;i<=n;i++) {
for(int j=a[i];j<=n;j++) {
dp[i][j]=dp[i][j-1];
if(!vis[j]) continue;
dp[i][j]=(dp[i-1][j]+dp[i][j])%mod;
}
}
for(int i=1;i<=n;i++) {
cout<<dp[i][n];
putchar('\n');
}
return 0;
}
[AGC005D] ~K Perm Counting
还是数数
直接考虑不好搞,考虑容斥,设 \(f_m\) 为含有至少 \(m\) 处 \(|P_i-i|=k\)
答案即为 $ \sum_{i=0}^{n}f_i$
考虑如何计算。
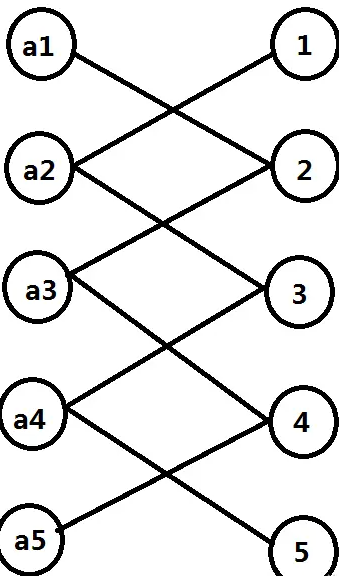
我们可以把它画出一张图,左边的表示位置,右边的表示权值,所以当 \(k=1\) 时,上图中的所以边都会使 \(|P_i-i|=k\) , 我们可以把上图看成一条条的链,在一条链上,选择相邻的两个节点,会使 \(|P_i-i|=k\) , 一个节点只能连出一条边,
所以我们根据这个来列状态转移方程。
设 \(dp_{i,j,0/1}\) 表示考虑到第 \(i\) 个节点,已经连了 \(j\) 条边,且第 \(i\) 个节点是否与第 \(i-1\) 个节点连边。
显然有:
$$ dp_{i,j,0}=dp_{i-1,j,0}+dp_{i-1,j,1} $$
$$ dp_{i,j,1}=dp_{i-1,j-1,0} $$
注意一条链的开头是不可以连边的,特判一下就可以了。
最后的答案为 $ \sum_{i=0}^{n}!(n-i)·dp_{2n,i} $
复杂度为 \(O(n^2)\)
据说可以使用多项式科技可以优化到 \(O(n\log n)\)
点击查看代码
#include <iostream>
#include <cstdio>
#include <cmath>
#define int long long
const int mod=924844033;
const int MAXN=4010;
using namespace std;
inline int read() {
int f=1,x=0;
char ch=getchar();
while(ch>'9' || ch<'0') {
if(ch=='-') {
f=-1;
}
ch=getchar();
}
while(ch>='0' && ch<='9') {
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return f*x;
}
int n,k,cnt;
int dp[MAXN<<1][MAXN][2];
int jc[MAXN],ans,vis[MAXN<<1];
void init() {
jc[0]=1;
for(int i=1;i<=n;i++) {
jc[i]=jc[i-1]*i%mod;
}
}
signed main() {
n=read() ,k=read();
init();
for(int i=1;i<=k;i++) {
for(int p=0;p<=1;p++) {
for(int j=i;j<=n;j+=k) {
cnt++;
if(i!=j) vis[cnt]=1;
}
}
}
dp[0][0][0]=1;
for(int i=1;i<=(n<<1);i++) {
for(int j=0;j<=n;j++) {
dp[i][j][0]=(dp[i-1][j][0]+dp[i-1][j][1])%mod;
if(vis[i] && j) {
dp[i][j][1]=dp[i-1][j-1][0]%mod;
}
}
}
ans=0;
for(int i=0;i<=n;i++) {
if(i&1) {
ans=((ans-jc[n-i]%mod*(dp[n<<1][i][0]+dp[n<<1][i][1])%mod)+mod)%mod;
}
else {
ans=((ans+jc[n-i]%mod*(dp[n<<1][i][0]+dp[n<<1][i][1])%mod)+mod)%mod;
}
}
cout<<ans%mod;
return 0;
}

