数据结构之栈(Java,C语言的实现)以及相关习题巩固

合集 - 算法(3)
1.分治法介绍(以及在棋盘覆盖问题的使用)2.数据结构 顺序表(C语言 与 Java实现)以及部分练习题
3.数据结构之栈(Java,C语言的实现)以及相关习题巩固
收起

目录

栈

概念以及代码实现

栈是仅限于在表尾进行插入和删除的线性表,它遵循先进后出,后进先出原则

  • 所以可以在递归,判断回文,反转链表.......

image-20240530132703003

代码实现部分java

public interface Stack_i <T>{
    //入栈
    void push(T e);
    //出栈
    T pop();
    //获取栈顶元素
    T peek();
    //获取栈的元素个数
    int size();
    //栈是否为空
    boolean isEmpty();
}

import java.util.Random;
public class MyArr<T> {

    private int capacity = 0;
    private int size = 0;
    private T[] arr;

    public MyArr(int capacity) {
        if (capacity < 0) this.capacity = 10; //if no right input, we will initial capacity 10
        this.capacity = capacity;
        this.arr = (T[]) new Object[capacity];
    }

    public int getCapacity() {
        return capacity;
    }

    public int getSize() {
        return size;
    }

    public T[] setCapacity(int capacity) {
        if (capacity < 0) {
            throw new RuntimeException("扩大小异常");
        }
        this.capacity = capacity;
        T[] newNum = (T[]) new Object[capacity];
        for (int i = 0; i < this.size; ++i) {
            newNum[i] = this.arr[i];
        }
        return newNum;
    }

    //增加元素
    public void add(T val) {
        if (this.size >= this.capacity) {
            this.arr = setCapacity(2 * this.capacity);
        }
        this.arr[this.size++] = val;
    }
    //数组末尾增加元素
    public void addLst(T val){
        this.add(val);
    }

    //删除元素
    public  T removeByIndex(int index) {
        if (index < 0 || index > this.capacity) {
            throw new RuntimeException("数组越界");
        }
        for (int i = index; i < size - 1; ++i) {
            arr[i] = arr[i + 1];
        }
        size--;
        if (size < this.capacity / 4 && this.capacity > 4) {
            arr = setCapacity(this.capacity / 4);
        }
        return this.arr[index];
    }
    //删除数组末尾元素
    public T removeLast(){
        return this.removeByIndex(this.size-1);
    }
    //修改位置元素
    public void modify(int index, T val) {
        if (index < 0 || index > size - 1) {
            throw new RuntimeException("数组越界");
        }
        arr[index] = val;
    }

    //获取某元素位置
    public int locateVal(T val) {
        for (int i = 0; i < size; ++i) {
            if (arr[i] == val) {
                return i;//return index
            }
        }
        // if no find return -1
        return -1;
    }
    //获取尾元素
    public T getLast(){
        return this.arr[this.size-1];
    }
    //打印元素


    @Override
    public String toString() {
        StringBuffer stringBuffer = new StringBuffer();
        stringBuffer.append('[');
        for (int i = 0; i < this.size - 1; ++i) {
            stringBuffer.append(arr[i] + ",");
        }
        if(size>0) stringBuffer.append(arr[size - 1]);
        stringBuffer.append(']');
        return stringBuffer.toString();
    }

}


public class StackImplement<T> implements Stack_i<T>{

    private MyArr<T> data;
    private int size=0;
    @Override
    public void push(T e) {
        this.size++;
        this.data.addLst(e);
    }

    public StackImplement() {
        data = new MyArr<>(10);
    }

    @Override
    public T pop() {
        if(this.isEmpty()){
            throw new RuntimeException("栈为空");
        }
        return this.data.removeLast();
    }

    @Override
    public T peek() {
        return this.data.getLast();
    }

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        if(size==0)return true;
        return false;
    }
    public int getCapacity(){
        return this.data.getCapacity();
    }
}

c语言实现(顺序栈)

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define OVERFLOW 0
#define MAXSIZE 10
typedef int Status;
typedef int Element;

//声明栈的顺序结构定义
typedef struct {
	Element* base;
	Element* top;
	int stackSize;
}SqStack;
//栈的功能
Status InitStack(SqStack* S);//初始化栈
Status Push(SqStack* S, Element e);//入栈操作
Status Pop(SqStack* S, Element* e);//出栈操作,并返回出去的值
Status IsEmpty(SqStack S);//判断栈是否为空
void PrintStack(SqStack S);//打印栈
Status OperateMenu();//用户界面选择
Element GetTop(SqStack S);//获取头元素
void DestroyStack(SqStack* S);//销毁链表
Status ClearStack(SqStack* S);//清理栈中元素
int StackLen(SqStack S);//获取栈长度

int main() {
	SqStack S;
	/*
	赋值为NULL，确保变量具有一个初始状态，避免出现潜在问题,如果没有初始化，
	系统会分配一个随机地址，在后面对指针修改访问时可能会程序崩溃
	*/
	S.base = NULL;
	S.top = NULL;
	S.stackSize = 0;
	int choice;//记录用户选择
	Element e;//元素类型
	int temp = 0;//接受函数返回值
	int len;//获取栈长度
	while (OK) {
		choice = OperateMenu();
		switch (choice)
		{
		case 1:
			InitStack(&S);
			printf("初始化栈\n");
			break;
		case 2:
			printf("请输入要入栈的元素\n");
			scanf("%d", &e);
			temp = Push(&S, e);
			if(temp==-1){
				printf("此栈未被初始化！\n");
				break;
			}
			printf("入栈成功!\n");
			PrintStack(S);//打印元素
			break;

		case 3:
			temp = Pop(&S, &e);
			if(temp==-1){
				printf("此栈未被初始化！\n");
				break;
			}
			if (temp == ERROR) {
				printf("栈空!\n");
				break;
			}
			printf("出栈的元素为:%d\n", e);
			PrintStack(S);
			break;

		case 4:
			temp = IsEmpty(S);
			if(temp==-1){
				printf("此栈未被初始化！\n");
				break;
			}
			if (temp == ERROR) {
				printf("不为空栈!\n");
				PrintStack(S);
				break;
			}
			printf("为空栈\n");
			break;
		case 5:
			PrintStack(S);
			break;
		case 6:
			e = GetTop(S);
			if(e==-2){
				printf("此栈未被初始化！\n");
				break;
			}
			if (e == -1) {
				printf("为空栈\n");
				break;
			}
			printf("栈顶元素为: %d\n", e);
			PrintStack(S);
			break;
		case 7:
			temp = ClearStack(&S);
			if(temp==-1){
				printf("此栈未被初始化！\n");
				break;
			}
			printf("清理成功!\n");
			break;
		case 8:
			len = StackLen(S);
			if(len == -1){
				printf("此栈未被初始化！\n");
				break;
			}
			printf("链表长度为:%d\n", len);
			PrintStack(S);
			break;
		case 9:
			DestroyStack(&S);
			printf("销毁成功\n");
			break;
		default:
			exit(OVERFLOW);
		}

	}
	return 0;
}
Status InitStack(SqStack* S) {
	S->base = (Element*)malloc(sizeof(Element) * MAXSIZE);
	if (S->base == NULL) {
		exit(OVERFLOW);//申请失败,异常结束程序
	}
	S->top = S->base;
	S->stackSize = MAXSIZE;
	//申请成功
	return OK;
}
Status Push(SqStack* S,Element e) {
	//判断栈是否初始化
	if(S->top==NULL||S->base==NULL){
		printf("此栈未被初始化！\n");
		return -1;
	}
	//判断栈是否满
	if (S->top - S->base == S->stackSize) {
		S->base = (Element*)realloc(S->base, sizeof(Element) * MAXSIZE);
		S->stackSize += MAXSIZE;
		S->top = S->base + MAXSIZE;
	}
	*(S->top) = e;
	S->top++;
	//插入完毕
	return OK;
}
Status Pop(SqStack* S, Element* e) {
	if(S->top==NULL||S->base==NULL)return -1;//此栈未被初始化
	if (S->top == S->base)return ERROR;//此时为空栈
	*e = *(--S->top);
	//出栈成功
	return OK;
}
Status IsEmpty(SqStack S) {
	if(S.top==NULL||S.base==NULL)return -1;//此栈未被初始化
	if (S.base == S.top)return OK;//判断空栈
	else return ERROR;
}
void PrintStack(SqStack S) {
	if(S.top==NULL||S.base==NULL){
		printf("此栈未被初始化\n");
		return;//此栈未被初始化
	}
	if (S.base == S.top) {
		printf("此栈为空栈\n");
		return;
	}
	
	Element* ptr = --S.top;
	while (ptr!=S.base) {
		printf("%d\t", *ptr);
		--ptr;
	}
	//打印栈底元素
	printf("%d", *S.base);
	printf("\n");
	return;
}
Status OperateMenu() {
	int choice = 0;//记录用户选择
	printf("----------------欢迎使用栈----------------\n");
	printf("----------------1.初始化栈----------------\n");
	printf("----------------2.入栈操作----------------\n");
	printf("----------------3.出栈操作----------------\n");
	printf("----------------4.判断栈是否为空----------\n");
	printf("----------------5.打印栈------------------\n");
	printf("----------------6.获取头元素--------------\n");
	printf("----------------7.清空列表元素------------\n");
	printf("----------------8.获取栈的长度------------\n");
	printf("----------------9.销毁栈------------------\n");
	printf("----------------10.退出--------------------\n");
	printf("----------------请输入选项----------------\n");
	scanf("%d", &choice);
	return choice;

}
Element GetTop(SqStack S) {
	if(S.top==NULL||S.base==NULL)return -2;//此栈未被初始化
	if (S.base == S.top) return -1;	
	return *(--S.top);
}
void DestroyStack(SqStack* S) {
	S->base = NULL;
	S->top = NULL;
	S->stackSize = 0;
}
Status ClearStack(SqStack* S) {
	if(S->top==NULL||S->base==NULL)return -1;//此栈未被初始化
	if (S->top == S->base)return ERROR;//空表
	S->top = S->base;
	return OK;
}
int StackLen(SqStack S) {
	if(S.top==NULL||S.base==NULL)return -1;//此栈未被初始化
	return S.top - S.base;
}

例题

232. 用栈实现队列

1614. 括号的最大嵌套深度

给定 有效括号字符串 s，返回 s 的 嵌套深度。嵌套深度是嵌套括号的 最大 数量。

示例 1：

输入：s = "(1+(2*3)+((8)/4))+1"

输出：3

解释：数字 8 在嵌套的 3 层括号中。

示例 2：

输入：s = "(1)+((2))+(((3)))"

输出：3

解释：数字 3 在嵌套的 3 层括号中。

示例 3：

输入：s = "()(())((()()))"

输出：3

提示：

  • 1 <= s.length <= 100
  • s 由数字 0-9 和字符 '+'、'-'、'*'、'/'、'('、')' 组成
  • 题目数据保证括号字符串 s 是 有效的括号字符串
java
    
class Solution {
    public int maxDepth(String s) {
        // 使用top表示栈顶指针
        int top = 0;
        // 记录括号数量
        int res = 0;
        for (int i = 0; i < s.length(); ++i) {
            // 如果碰见左括号说明 括号深度增加 即入栈
            if (s.charAt(i) == '(') {
                ++top;
                // 记录最大深度
                if (top > res) {
                    res = top;
                }
                // 碰到右括号出栈 深度就减少
            } else if (s.charAt(i) == ')') {
                --top;
            }
        }
        return res;
    }
}

234. 回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为

回文链表

。如果是，返回 true ；否则，返回 false 。

示例 1：

img

输入：head = [1,2,2,1]
输出：true

示例 2：

img

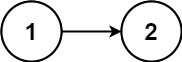
输入：head = [1,2]
输出：false

提示：

  • 链表中节点数目在范围[1, 105] 内
  • 0 <= Node.val <= 9

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
     public boolean isPalindrome(ListNode head) {
        // 利用栈的先进后出原则 
        /*
        可以把链表节点都入栈 然后逐一出栈 栈底指针与栈顶指针对比元素即可
         */
        int[] stack = new int[100001];
        int base = 0;
        int top = 0;
        ListNode p = head;
        while (p != null) {
            stack[top++] = p.val;
            p = p.next;
        }
        --top;
        while(base<=top){
            if(stack[base]!=stack[top])return false;
            base = base+1;
            top = top-1;
        }
        return true;
    }
}

1614. 括号的最大嵌套深度

LCR 123. 图书整理 I

206. 反转链表

402. 移掉 K 位数字

844. 比较含退格的字符串

LCR 036. 逆波兰表达式求值

[面试题 03.01. 三合一](

posted @   Yang0710  阅读(15)  评论(0)  编辑  收藏  举报
相关博文：
· 数据结构 顺序表(C语言 与 Java实现)以及部分练习题
· Java 集合的概念
· 栈(顺序)的实现：括号的解析
· 栈（stack）是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫做栈的顶（top），它是后进先出（LIFO）的
· 数据结构之线性结构-栈
阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 开源Multi-agent AI智能体框架aevatar.ai，欢迎大家贡献代码
· Manus重磅发布：全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· AI技术革命，工作效率10个最佳AI工具
  1. 1 イエスタデイ（翻自 Official髭男dism） 茶泡饭,春茶,kobasolo
  2. 2 世间美好与你环环相扣 柏松
世间美好与你环环相扣 - 柏松
00:00 / 00:00
An audio error has occurred, player will skip forward in 2 seconds.

作词 : 尹初七

作曲 : 柏松

编曲 : 彭圣杰

偏偏秉烛夜游

偏偏秉烛夜游

午夜星辰 似奔走之友

爱你每个结痂伤口

酿成的陈年烈酒

入喉尚算可口

入喉尚算可口

怎么泪水 还偶尔失守

邀你细看心中缺口

裂缝中留存 温柔

此时已莺飞草长 爱的人正在路上

此时已莺飞草长 爱的人正在路上

我知他风雨兼程 途经日暮不赏

穿越人海 只为与你相拥

此刻已皓月当空 爱的人手捧星光

我知他乘风破浪 去了黑暗一趟

感同身受 给你救赎热望

知道你不能 还要你感受

知道你不能 还要你感受

让星光加了一点彩虹

让樱花偷偷 吻你额头

让世间美好 与你环环相扣

此时已莺飞草长 爱的人正在路上

此时已莺飞草长 爱的人正在路上

我知他风雨兼程 途经日暮不赏

穿越人海 只为与你相拥

此刻已皓月当空 爱的人手捧星光

我知他乘风破浪 去了黑暗一趟

感同身受 给你救赎热望

此时已莺飞草长 爱的人正在路上

此时已莺飞草长 爱的人正在路上

我知他风雨兼程 途经日暮不赏

穿越人海 只为与你相拥

此刻已皓月当空 爱的人手捧星光

我知他乘风破浪 去了黑暗一趟

感同身受 给你救赎热望

知道你不能 还要你感受

知道你不能 还要你感受

让星光加了一点彩虹

当樱花开的纷纷扬扬

当世间美好 与你环环相扣

特别鸣谢：槿葵，我们的海报制作妹妹。

原唱：柏松

吉他：柏松

和声：柏松

录音：柏松

混音：张强

点击右上角即可分享
微信分享提示
AI IDE Trae