树分治入门 POJ1741,hdu5977

经常发现一些布布扣一类的网站直接爬csdn的blog，娘的

原文地址在这http://blog.csdn.net/cww97/article/details/77506430

树分治讲解

对于树上的路径问题，一种高效的处理方式就是分治算法。关于树分治算法的研究，详见2009年IOI国家集训队论文——《分治算法在树的路径问题中的应用》。
通常对于树上的分治算法有两种，第一种是针对点进行的分治，另一种是针对边进行的分治，可以证明，大部分情况下点分治算法的性能更加稳定，而边分治在某些情况下，算法效率非常低。所以以下主要讨论点分治。
如POJ-1741,求解一棵树中路径长度不大于K的有多少点对。
对于一棵有根树，树中满足对所对应的一条路径，必然是以下两种情况之一：
1.经过根节点
2.路径在以根节点某个儿子为根的一棵子树中
对于情况2，可以递归求解，下面主要来考虑情况1.
那么对于这道题的情况1，设dis[i]为节点i到根的距离，我们就是要求解有多少对经过根的路径，那么问题等价于能找到多少对不同的点对(i,j)，使得dis[i]+dis[j]<=k，而且i和j要属于以当前根的两个不同的儿子为根的子树中。
将问题转化以下，就可以发现所求结果等价于在一棵有根树中找到的点对数x-在以当前根的儿子为根的子树所找到的点对数。
求X、Y的过程均可以转化为以下问题：已知A[1],A[2],…A[m]，求满足i

poj1741

论文里第一道例题

参考了网上的两个板

kuangbin的solve写的很csy，这一部分用了这个

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4 + 7;
const int INF = 0x3f3f3f3f;
int n, k, ans;

struct Edge{
    int from, to, w, nxt;
    Edge(){}
    Edge (int f, int t, int _w, int n):from(f),to(t),w(_w),nxt(n){}
} edges[N * 2];
bool vis[N];
int head[N], E, siz[N], dep[N];

void Init(){
    E = 0;
    memset(head, -1, sizeof(head));
    memset(vis, false, sizeof(vis));
}
void AddEdge(int u,int v,int w){
    edges[E] = Edge(u, v, w, head[u]);
    head[u] = E++;
}

int dfssize(int u, int pre){
    siz[u] = 1;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        siz[u] += dfssize(e.to, u);
    }
    return siz[u];
}

//找重心
void dfsroot(int u, int pre, int totnum, int &minn, int &root){
    int maxx = totnum - siz[u];
    for (int i = head[u]; i != -1;i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to]) continue;
        dfsroot(e.to, u, totnum, minn, root);
        maxx = max(maxx, siz[e.to]);
    }
    if(maxx < minn){minn = maxx; root = u;}
}

//求每个点离重心的距离
void dfsdep(int u,int pre,int dist, int &num){
    dep[num++] = dist;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        dfsdep(e.to, u, dist + e.w, num);
    }
}

//计算以u为根的子树中有多少点对的距离小于等于K
int calc(int u, int d){
    //printf("calc(%d, %d)\n", u, d);
    int ans = 0, num = 0;
    dfsdep(u, -1, d, num);
    sort(dep, dep + num);
    int i = 0, j = num - 1;
    for (; i < j; i++){
        while (dep[i]+dep[j]>k && i<j) j--;
        ans += j - i;
    }
    return ans;
}

void solve(int u){
    int Max = N, root, minn = INF;
    int totnum = dfssize(u, -1);
    dfsroot(u, -1, totnum, minn, root);
    ans += calc(root, 0);
    vis[root] = 1;
    for(int i = head[root]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if (vis[e.to]) continue;
        ans -= calc(e.to, e.w);
        solve(e.to);
    }
}

int main(){
    ///freopen("in.txt","r",stdin);
    int u, v, w;
    for (; ~scanf("%d%d", &n, &k) && (n|k);){
        Init();
        for(int i = 1; i < n; i++){
            scanf("%d%d%d", &u, &v, &w);
            AddEdge(u, v, w);
            AddEdge(v, u, w);
        }
        ans = 0;
        solve(1);
        printf("%d\n", ans);
    }
    return 0;
}

2016ICPC大连 hdu5977

现场的时候k = 7，树形dp可以水过，重现赛的时候k改为了10

需要树分治，裸的树分治（如上），统计距离小于等于k的点对数

本题问路径经包含所有颜色的点对数

利用位运算状压，k种颜色，k<=10，每种颜色占一位

原题转化为统计路径 or运算和 == fullk的点对数

fullk = (1<<k) - 1;

poj1741通过一个sort和两个指针统计出了dist<=k的点对数

这里是二进制位，sort不灵了，需要另一种nlogn的方案

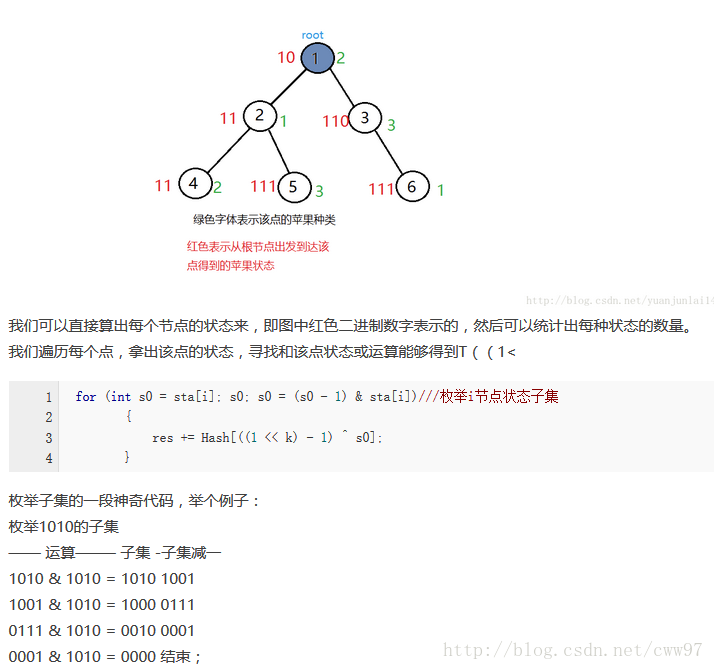
对于每点u的状态dep[u]，枚举其每个子集s0，ans += hash[fullk ^ so]

枚举子集一开始也不会，很玄学，这里有一些讲解，骚到了

位运算状压其实很好想，把原来的加号改成or运算就好了

很骚的一段就是calc中的一段，从这里再次盗个图来，举了个枚举子集的例子

我见他代码第一行是

/**此代码借鉴了某大神的，我看懂了后又分析的*/

似乎他也参考了这个blog

扯了一堆有的没的

最后贴自己的代码吧，用上题的板子改，dfsdep和dfs看着改就好，calc动些脑子

#include <map>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 5e4 + 7;
const int INF = 0x3f3f3f3f;
int n, k;
LL ans;
int col[N], fullk;
LL hashS[1200];

struct Edge{
    int from, to, w, nxt;
    Edge(){}
    Edge (int f, int t, int _w, int n):from(f),to(t),w(_w),nxt(n){}
} edges[N * 2];
bool vis[N];
//本题中边无w，dep为节点到root col or运算和
int head[N], E, siz[N], dep[N];

void Init(){
    E = 0; fullk = (1<<k) - 1;
    memset(head, -1, sizeof(head));
    memset(vis, false, sizeof(vis));
}
void AddEdge(int u,int v,int w){
    edges[E] = Edge(u, v, w, head[u]);
    head[u] = E++;
}

int dfssize(int u, int pre){
    siz[u] = 1;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        siz[u] += dfssize(e.to, u);
    }
    return siz[u];
}

//找重心
void dfsroot(int u, int pre, int totnum, int &minn, int &root){
    int maxx = totnum - siz[u];
    for (int i = head[u]; i != -1;i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to]) continue;
        dfsroot(e.to, u, totnum, minn, root);
        maxx = max(maxx, siz[e.to]);
    }
    if(maxx < minn){minn = maxx; root = u;}
}

//求每个点离重心的距离
void dfsdep(int u, int pre, int dist, int &num){
    //printf("u = %d, num = %d, dist = %d\n", u, num, dist);
    dep[num++] = dist;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        dfsdep(e.to, u, dist | (1<<col[e.to]), num);
    }
}

//计算以u为根的子树中有多少点对的距离小于等于K, 经过u
LL calc(int u, int d){ //d为基础距离
    //printf("calc(%d, %d)\n", u, d);
    LL ans = 0;
    int num = 0;
    dfsdep(u, -1, d, num);
    memset(hashS, 0, sizeof(hashS));
    for (int i = 0; i < num; i++) hashS[dep[i]]++;
    for (int i = 0; i < num; i++){
        hashS[dep[i]]--;
        ans += hashS[fullk];
        for (int s0 =  dep[i]; s0; s0 = (s0-1) & dep[i]){
            ans += hashS[fullk ^ s0];
        }
        hashS[dep[i]]++;
    }
    return ans;
}

void dfs(int u){
    int root, minn = INF;
    int totnum = dfssize(u, -1);
    dfsroot(u, -1, totnum, minn, root);
    //printf("---------> root = %d\n", root);
    ans += calc(root, 1<<col[root]);
    //printf("ans = %d\n", ans);
    vis[root] = 1;
    for(int i = head[root]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if (vis[e.to]) continue;
        ans -= calc(e.to, (1<<col[root]) | (1<<col[e.to])); //减去重复部分，即没必要经过u的
        //printf("ans = %d\n", ans);
        dfs(e.to);                             //在下一层dfs中解决
    }
}

int main(){
    //freopen("in.txt", "r", stdin);
    int u, v;
    for (; scanf("%d%d", &n, &k) == 2;){
        Init();
        for (int i = 1; i <= n; i++) {
            scanf("%d", &col[i]);
            col[i]--;
        }
        for (int i = 1; i < n; i++){
            scanf("%d%d", &u, &v);
            AddEdge(u, v, 0);
            AddEdge(v, u, 0);
        }
        ans = 0;
        if (k == 1) ans = (LL)n * (LL)n;
        else dfs(1);
        printf("%lld\n", ans);
    }
    return 0;
}

一个子集枚举的小题目

poj2531，给个20个点的图，问最小割

还有点迷糊这个怎么就能剪枝了

#include <cstdio>
#include <algorithm>
using namespace std;

int main(){
    int n, g[20][20];
    scanf("%d", &n);
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            scanf("%d", &g[i][j]);
    int ans = 0;
    //剪枝就是把i++改成了i+=2，让i总是奇数
    for(int i = 1; i < (1<<n); i += 2){
        int sum = 0;
        for (int j = 0; j < n; j++) if (i & (1<<j)){
            for(int k = 0; k < n; k++)
                if ((~i) & (1<<k)) sum += g[j][k];
        }
        ans = max(ans, sum);
    }
    printf("%d\n", ans);
    return 0;
}

这题正解好像是dfs

不过，随机化乱搞似乎也可以，乱搞好玩啊，here

操作1e5次
对于每一次操作，随机选择一个点，把他放到另一个集合里面去，然后for一遍，算出当前的割值sum，再与记录的最大值ans比较更新

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int n, g[22][22];
bool go[22];

int main(){
    for (; ~scanf("%d", &n);){
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                scanf("%d", &g[i][j]);

        memset(go, 0, sizeof(0));
        int _ = 1e5, sum = 0, ans = 0;
        for (; _--;){
            int t = rand() % n;
            go[t] ^= 1;
            for (int i = 0; i < n; i++){
                if (go[t] ^ go[i]) sum += g[t][i];
                else sum -= g[t][i];
            }
            ans = max(sum, ans);
        }
        printf("%d\n", ans);
    }
    return 0;
}