机器学习作业笔记
Assignment2: mds & isomap
陈伟文 10152510217
指导教师:金博
问题
实现mds算法和isomap算法
数据
sklearn生成的三维点的数据,抄书上的
似乎墙筑高了,好多vpn炸了,uci上不去了,不知道后续作业的数据该如何
def get_data():
return datasets.samples_generator.make_s_curve(200, random_state=0)公式们
算法概述
MDS
isomap
数据预处理
计算距离矩阵
def get_dis(mat, kk):
"""
generate the distance matrix of the graph
:param mat: the position of the points
:param kk: the number of neighbors we get
:return: the distance matrix
"""
n = len(mat)
m = len(mat[0])
ans = np.zeros((n, n))
for i in range(n):
for j in range(n):
ans[i][j] = sqrt(sum(sqr(mat[i][k] - mat[j][k]) for k in range(m)))
sor = sorted(ans[i])
tmp = sor[kk - 1]
for j in range(n):
if ans[i][j] > tmp:
ans[i][j] = INF
return ansfloyed计算多源最短路
def floyed(d):
"""
shortest path algorithm: o(n^3)
:param d: distance matrix
:return: shortest distance matrix
"""
n = len(d)
for k in range(n):
for i in range(n):
for j in range(n):
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
return d核心代码
mds
def mds(dist, d, color):
"""
need I say something more?
:param dist: distance matrix
:param d: dimensionality
:param color: as you know
:return: new coordinate after dimensionality reduction
"""
n = len(dist)
disti = np.zeros(n)
distj = np.zeros(n)
for i in range(n): # formula 10.7
disti[i] = (1./n) * sum(sqr(dist[i][j]) for j in range(n))
for j in range(n): # formula 10.8
distj[j] = (1./n) * sum(sqr(dist[i][j]) for i in range(n))
# formula 10.9
dists = (1./(n*n)) * sum(sqr(dist[i][j]) for i in range(n) for j in range(n))
# formula 10.10
B = np.zeros((n, n))
for i in range(n):
for j in range(n):
B[i][j] = -1./2 * (sqr(dist[i][j]) - disti[i] - distj[j] + dists)
# decomposition B
eig_val, eig_vec = np.linalg.eig(B)
val = sorted(eig_val, reverse=True)
arg_list = np.argsort(-eig_val)
vec = np.zeros((n, n))
col = np.zeros(len(color))
# sort
for i in range(n):
vec[i] = eig_vec[arg_list[i]].real
col[i] = color[arg_list[i]]
ans = np.dot(vec[:, :d], np.diag(np.sqrt(val[:d])))
return ans, colmain
def main():
data, color = get_data()
print(color)
fig = plt.figure()
ax = fig.add_subplot(121, projection='3d')
plt.title('3d data')
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=color)
dis_mat = get_dis(data, 10)
dis_mat = floyed(dis_mat)
res, col = mds(dis_mat, 2, color)
ax = fig.add_subplot(122)
plt.title('isomap_data')
ax.scatter(res[:, 0].real, res[:, 1].real, c=col)
plt.show()运行结果
可以看出,很明显将三维坐标里的S形状的曲面拉成了一个平面
origin data是三维的,可以转,于是乎
头文件
# -*-encoding:utf-8-*-
"""
Machine Learning
homework2 mds & isomap
cww97 10152510217
2017/10/11
"""
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from numpy import square as sqr
from math import sqrt
import mpl_toolkits.mplot3d
INF = 0x3f3f3f3fAssignment3: 数据中心化
陈伟文 10152510217
2017/10/15
关于中心化
因为上课没认真听(划掉),百度了一波,看见了彭先生的blog,还有这个知乎
以PCA为例说下中心化的作用。
下面两幅图是数据做中心化(centering)前后的对比,可以看到其实就是一个平移的过程,平移后所有数据的中心是(0,0).
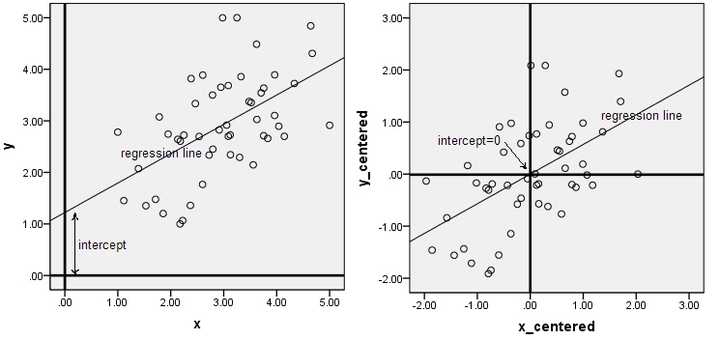
在做PCA的时候,我们需要找出矩阵的特征向量,也就是主成分(PC)。比如说找到的第一个特征向量是a = [1, 2],a在坐标平面上就是从原点出发到点(1,2)的一个向量。如果没有对数据做中心化,那算出来的第一主成分的方向可能就不是一个可以“描述”(或者说“概括”)数据的方向了。还是看图比较清楚。
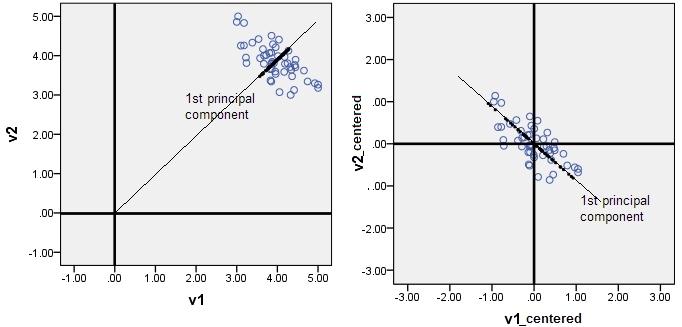
黑色线就是第一主成分的方向。只有中心化数据之后,计算得到的方向才能比较好的“概括”原来的数据。黑色线就是第一主成分的方向。只有中心化数据之后,计算得到的方向才能比较好的“概括”原来的数据。
回头看题目
在对高维数据降维前应先进行“中心化”,常见方法是将协方差矩阵
XXT 转换为XHHTXT ,其中H=I−1m11T,分析其效果
主要分析H,中心化的作用就是减掉平均值
把H带入原式,则
期中
若数据
则
记
继续算下去,
现在可以看出这个结果了:
实现了
至于(可能是因为上课神游了)
老师下次讲题目的时候能不能提一下协方差矩阵啊
assignment4: 决策树
标签(空格分隔): 机器学习
Problem
4.6 试选择4个UCI数据集,对上述3种算法所产生的未剪枝、预剪枝、后剪枝决策树进行实验比较,并进行适当的统计显著性检验
决策树算法
(from 书74页)
输入:
训练集
属性集
过程:
生成节点 node
if D 中样本全属于同一类别C then
将node 标记为 C 类节点; return
end if
if A == None or D 中样本在A上取值相同 then
将 node 标记为叶节点,其类别标记为 D 中样本数最多的类; return
end if
从 A 中选择最优划分属性 a[*];
for a[*] 的每个值 a[*][v] do:
为 node 生成一个分支; 令 D[v] 表示 D 在 a[*] 上取值为 a[*][v] 的样本子集;
if D[v] 为空 then
将分支标记为叶节点,其类别标记为 D 中样本最多的类; return
else
以 TreeGenerate(D[v], A \ {a[*]}) 为分支节点
end if
end for输出: 以 node 为根节点的一棵决策树
CART决策树 使用基尼指数(Gini Index)来选择划分属性。其公式如下:
先看眼结果吧
非常非常抱歉,因为人在外地,携带的电脑无力跑大规模数据,估统计学评估也没意义
三种剪枝的算法用树上的西瓜数据跑,
生成的决策树和树上的图一毛一样,说明我算法没写错,命要写没了
结论:
后剪枝决策树比起预剪枝决策树保留了更多的分支。在一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但同时其训练时间花销也比较大。
丑到不想看的代码
听说这次作业可以import现成的包,但是sklearn中的包剪枝并不方便
# -*- encoding: utf-8 -*-
from numpy import *
import pandas as pd
from treeplot import *
import copy
import re
# 计算数据集的基尼指数
def calc_Gini(dataset):
num_entries = len(dataset)
label_cnt = {}
# 给所有可能分类创建字典
for feat_vec in dataset:
current_label = feat_vec[-1]
if current_label not in label_cnt.keys():
label_cnt[current_label] = 0
label_cnt[current_label] += 1
Gini = 1.0
# 以2为指数计算香农熵
for key in label_cnt:
prob = float(label_cnt[key]) / num_entries
Gini -= prob * prob
return Gini
# 对离散变量划分数据集,取出该特征取值为 value 的所有样本
def split_data_set(dataset, axis, value):
ret_data_set = []
for feat_vec in dataset:
if feat_vec[axis] == value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_data_set.append(reduced_feat_vec)
return ret_data_set
# 对连续变量划分数据集,direction规定划分的方向,
# 决定是划分出小于value的数据样本还是大于value的数据样本集
def split_continuous_dataset(dataset, axis, value, direction):
ret_data_set = []
for feat_vec in dataset:
if direction == 0:
if feat_vec[axis] > value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_data_set.append(reduced_feat_vec)
else:
if feat_vec[axis] <= value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_data_set.append(reduced_feat_vec)
return ret_data_set
# 选择最好的数据集划分方式
def choose_best_feature_to_split(dataset, labels):
num_features = len(dataset[0]) - 1
best_Gini_index = 100000.0
best_feature = -1
best_split_dict = {}
for i in range(num_features):
feat_list = [example[i] for example in dataset]
# 对连续型特征进行处理
if type(feat_list[0]).__name__ == 'float' or type(feat_list[0]).__name__ == 'int':
# 产生n-1个候选划分点
sort_feat_list = sorted(feat_list)
split_list = []
for j in range(len(sort_feat_list) - 1):
split_list.append((sort_feat_list[j] + sort_feat_list[j + 1]) / 2.0)
best_split_Gini = 10000
slen = len(split_list)
# 求用第j个候选划分点划分时,得到的信息熵,并记录最佳划分点
for j in range(slen):
value = split_list[j]
new_Gini_index = 0.0
sub_dataset0 = split_continuous_dataset(dataset, i, value, 0)
sub_dataset1 = split_continuous_dataset(dataset, i, value, 1)
prob0 = len(sub_dataset0) / float(len(dataset))
new_Gini_index += prob0 * calc_Gini(sub_dataset0)
prob1 = len(sub_dataset1) / float(len(dataset))
new_Gini_index += prob1 * calc_Gini(sub_dataset1)
if new_Gini_index < best_split_Gini:
best_split_Gini = new_Gini_index
best_split = j
# 用字典记录当前特征的最佳划分点
best_split_dict[labels[i]] = split_list[best_split]
Gini_index = best_split_Gini
# 对离散型特征进行处理
else:
unique_vals = set(feat_list)
new_Gini_index = 0.0
# 计算该特征下每种划分的信息熵
for value in unique_vals:
sub_dataset = split_data_set(dataset, i, value)
prob = len(sub_dataset) / float(len(dataset))
new_Gini_index += prob * calc_Gini(sub_dataset)
Gini_index = new_Gini_index
if Gini_index < best_Gini_index:
best_Gini_index = Gini_index
best_feature = i
# 若当前节点的最佳划分特征为连续特征,则将其以之前记录的划分点为界进行二值化处理
# 即是否小于等于best_split_value
if type(dataset[0][best_feature]).__name__ == 'float' or type(dataset[0][best_feature]).__name__ == 'int':
best_split_value = best_split_dict[labels[best_feature]]
labels[best_feature] = labels[best_feature] + '<=' + str(best_split_value)
for i in range(shape(dataset)[0]):
if dataset[i][best_feature] <= best_split_value:
dataset[i][best_feature] = 1
else:
dataset[i][best_feature] = 0
return best_feature
# 特征若已经划分完,节点下的样本还没有统一取值,则需要进行投票
def majority_cnt(class_list):
class_cnt = {}
for vote in class_list:
if vote not in class_cnt.keys():
class_cnt[vote] = 0
class_cnt[vote] += 1
return max(class_cnt)
# ------------------------------ for 预剪枝-------------------------------------
# 由于在Tree中,连续值特征的名称以及改为了 feature<=value的形式
# 因此对于这类特征,需要利用正则表达式进行分割,获得特征名以及分割阈值
def classify(inputTree, featLabels, testVec):
firstStr = list(inputTree.keys())[0]
if '<=' in firstStr:
featvalue = float(re.compile("(<=.+)").search(firstStr).group()[2:])
featkey=re.compile("(.+<=)").search(firstStr).group()[:-2]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(featkey)
if testVec[featIndex]<=featvalue:
judge = 1
else:
judge=0
for key in secondDict.keys():
if judge == int(key):
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
else:
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
return classLabel
# 测试决策树正确率
def testing(my_tree,data_test,labels):
error=0.0
for i in range(len(data_test)):
if classify(my_tree,labels,data_test[i])!=data_test[i][-1]:
error+=1
print('my_tree %d' %error)
return float(error)
# 测试投票节点正确率
def testingMajor(major,data_test):
error=0.0
for i in range(len(data_test)):
if major!=data_test[i][-1]:
error+=1
print('major %d' %error)
return float(error)
# -----------------------------end for 预剪枝--------------------------------------
# 主程序,递归产生决策树
def create_tree(dataset, labels, data_full, labels_full, data_test, pre_cut):
class_list = [example[-1] for example in dataset]
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
if len(dataset[0]) == 1:
return majority_cnt(class_list)
temp_labels = copy.deepcopy(labels)
best_feat = choose_best_feature_to_split(dataset, labels)
best_feat_label = labels[best_feat]
my_tree = {best_feat_label: {}}
if type(dataset[0][best_feat]).__name__ == 'str':
current_label = labels_full.index(labels[best_feat])
feat_values_full = [example[current_label] for example in data_full]
unique_vals_full = set(feat_values_full)
feat_values = [example[best_feat] for example in dataset]
unique_vals = set(feat_values)
del (labels[best_feat])
# 针对 best_feat 的每个取值,划分出一个子树。
for value in unique_vals:
sub_labels = labels[:]
if type(dataset[0][best_feat]).__name__ == 'str':
unique_vals_full.remove(value)
my_tree[best_feat_label][value] = create_tree(
split_data_set(dataset, best_feat, value), sub_labels, data_full, labels_full,
split_data_set(data_test, best_feat, value), pre_cut)
if type(dataset[0][best_feat]).__name__ == 'str':
for value in unique_vals_full:
my_tree[best_feat_label][value] = majority_cnt(class_list)
if pre_cut:
if testing(my_tree, data_test, temp_labels) < testingMajor(majority_cnt(class_list), data_test):
return my_tree
return majority_cnt(class_list)
else:
return my_tree
# --------------------------------后剪枝-------------------------------------
def postPruningTree(inputTree, dataSet, data_test, labels):
firstStr = list(inputTree.keys())[0]
secondDict=inputTree[firstStr]
classList=[example[-1] for example in dataSet]
featkey = copy.deepcopy(firstStr)
if '<=' in firstStr:
featkey = re.compile("(.+<=)").search(firstStr).group()[:-2]
featvalue=float(re.compile("(<=.+)").search(firstStr).group()[2:])
labelIndex = labels.index(featkey)
temp_labels=copy.deepcopy(labels)
del(labels[labelIndex])
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
if type(dataSet[0][labelIndex]).__name__=='str':
next_set = split_data_set(dataSet,labelIndex,key)
next_test = split_data_set(data_test,labelIndex,key)
inputTree[firstStr][key] = postPruningTree(secondDict[key], next_set, next_test, copy.deepcopy(labels))
else:
inputTree[firstStr][key] = postPruningTree(secondDict[key],\
split_continuous_dataset(dataSet,labelIndex, featvalue, key),\
split_continuous_dataset(data_test,labelIndex, featvalue, key),\
copy.deepcopy(labels))
if testing(inputTree,data_test,temp_labels)<=testingMajor(majority_cnt(classList),data_test):
return inputTree
return majority_cnt(classList)
# ------------------------------------------------------------------------------------------
def no_cut(data, labels, data_full, labels_full, data_test):
my_tree = create_tree(data, labels, data_full, labels_full, data_test, False)
createPlot(my_tree)
def pre_cut(data, labels, data_full, labels_full, data_test):
my_tree = create_tree(data, labels, data_full, labels_full, data_test, True)
print(my_tree)
createPlot(my_tree)
def post_cut(data, labels, data_full, labels_full, data_test):
my_tree = create_tree(data, labels, data_full, labels_full, data_test, False)
my_tree = postPruningTree(my_tree, data, data_test, labels_full)
createPlot(my_tree)
if __name__ == '__main__':
df = pd.read_csv('data/xigua.csv', sep='\t', encoding='utf-8')
data = df.values[:11, 1:].tolist()
data_full = data[:]
data_test = df.values[11:, 1:].tolist()
labels = df.columns.values[1:-1].tolist()
labels_full = labels[:]
#no_cut(data, labels, data_full, labels_full, data_test)
pre_cut(data, labels, data_full, labels_full, data_test)
# post_cut(data, labels, data_full, labels_full, data_test)treeplot.py
参考自网络
import matplotlib.pyplot as plt # 载入 pyplot API
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def getNumLeafs(myTree):
# 初始化树的叶子节点个数
numLeafs = 0
# myTree.keys() 获取树的非叶子节点'no surfacing'和'flippers'
# list(myTree.keys())[0] 获取第一个键名'no surfacing'
firstStr = list(myTree.keys())[0]
# 通过键名获取与之对应的值,即{0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}
secondDict = myTree[firstStr]
# 遍历树,secondDict.keys()获取所有的键
for key in secondDict.keys():
# 判断键是否为字典,键名1和其值就组成了一个字典,如果是字典则通过递归继续遍历,寻找叶子节点
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else: # 如果不是字典,则叶子结点的数目就加1
numLeafs += 1
return numLeafs # 返回叶子节点的数目
def getTreeDepth(myTree):
maxDepth = 0 # 初始化树的深度
firstStr = list(myTree.keys())[0] # 获取树的第一个键名
secondDict = myTree[firstStr] # 获取键名所对应的值
for key in secondDict.keys(): # 遍历树
#如果获取的键是字典,树的深度加1
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
#去深度的最大值
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth # 返回树的深度
#设置画节点用的盒子的样式
decisionNode = dict(boxstyle = "sawtooth",fc="0.8")
leafNode = dict(boxstyle = "round4",fc="0.8")
#设置画箭头的样式 http://matplotlib.org/api/patches_api.html#matplotlib.patches.FancyArrowPatch
arrow_args = dict(arrowstyle="<-")
#绘图相关参数的设置
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
# annotate函数是为绘制图上指定的数据点xy添加一个nodeTxt注释
# nodeTxt是给数据点xy添加一个注释,xy为数据点的开始绘制的坐标,位于节点的中间位置
# xycoords设置指定点xy的坐标类型,xytext为注释的中间点坐标,textcoords设置注释点坐标样式
# bbox设置装注释盒子的样式,arrowprops设置箭头的样式
'''
figure points:表示坐标原点在图的左下角的数据点
figure pixels:表示坐标原点在图的左下角的像素点
figure fraction:此时取值是小数,范围是([0,1],[0,1]),在图的左下角时xy是(0,0),最右上角是(1,1)
其他位置是按相对图的宽高的比例取最小值
axes points : 表示坐标原点在图中坐标的左下角的数据点
axes pixels : 表示坐标原点在图中坐标的左下角的像素点
axes fraction : 与figure fraction类似,只不过相对于图的位置改成是相对于坐标轴的位置
'''
createPlot.ax1.annotate(nodeTxt,xy=parentPt,\
xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',\
va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
# 绘制线中间的文字(0和1)的绘制
def plotMidText(cntrPt,parentPt,txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] #计算文字的x坐标
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] #计算文字的y坐标
createPlot.ax1.text(xMid,yMid,txtString)
# 绘制树
def plotTree(myTree,parentPt,nodeTxt):
#获取树的叶子节点
numLeafs = getNumLeafs(myTree)
#获取树的深度
depth = getTreeDepth(myTree)
#firstStr = myTree.keys()[0]
#获取第一个键名
firstStr = list(myTree.keys())[0]
#计算子节点的坐标
cntrPt = (plotTree.xoff + (1.0 + float(numLeafs))/2.0/plotTree.totalW,\
plotTree.yoff)
#绘制线上的文字
plotMidText(cntrPt,parentPt,nodeTxt)
#绘制节点
plotNode(firstStr,cntrPt,parentPt,decisionNode)
#获取第一个键值
secondDict = myTree[firstStr]
#计算节点y方向上的偏移量,根据树的深度
plotTree.yoff = plotTree.yoff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
#递归绘制树
plotTree(secondDict[key],cntrPt,str(key))
else:
#更新x的偏移量,每个叶子结点x轴方向上的距离为 1/plotTree.totalW
plotTree.xoff = plotTree.xoff + 1.0 / plotTree.totalW
#绘制非叶子节点
plotNode(secondDict[key],(plotTree.xoff,plotTree.yoff),\
cntrPt,leafNode)
#绘制箭头上的标志
plotMidText((plotTree.xoff,plotTree.yoff),cntrPt,str(key))
plotTree.yoff = plotTree.yoff + 1.0 / plotTree.totalD
#绘制决策树,inTree的格式为{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
def createPlot(inTree):
#新建一个figure设置背景颜色为白色
fig = plt.figure(1,facecolor='white')
#清除figure
fig.clf()
axprops = dict(xticks=[],yticks=[])
#创建一个1行1列1个figure,并把网格里面的第一个figure的Axes实例返回给ax1作为函数createPlot()
#的属性,这个属性ax1相当于一个全局变量,可以给plotNode函数使用
createPlot.ax1 = plt.subplot(111,frameon=False,**axprops)
#获取树的叶子节点
plotTree.totalW = float(getNumLeafs(inTree))
#获取树的深度
plotTree.totalD = float(getTreeDepth(inTree))
#节点的x轴的偏移量为-1/plotTree.totlaW/2,1为x轴的长度,除以2保证每一个节点的x轴之间的距离为1/plotTree.totlaW*2
plotTree.xoff = -0.5/plotTree.totalW
plotTree.yoff = 1.0
plotTree(inTree,(0.5,1.0),'')
# plt.title(title)
plt.show()参考文献
[1] scikit-learn学习 - 决策树 ——zhaoxianyu 博客园
[2] AttributeError: ‘list’ object has no attribute ‘write_pdf’——xyq_idata 博客园
[3] 安装GraphViz以供python调用——tina_ttl CSDN











 浙公网安备 33010602011771号
浙公网安备 33010602011771号