luogu4827 梦美的线段树

梦美的线段树 题解

写完被出题人喷代码丑了呜呜呜

---

题目链接点这

这题有点毒瘤啊，__int128才能过，建议食用洛谷ide

介于前面三篇的都比较玄学（代码都比较丑）,打算自己写一发

自己写的线段树常数应该比其他几篇大一点，为了方便理解吧

首先数学期望

$E = \sum P_i * sum_i = 一通操作 = \frac{\sum sum_i^2}{sum_{rt}}$

这一步应该比较好计算，同时相信大部分人都死在了这里比如我

然后想到这题不是线段树维护期望，而是维护区间平方和

对于一个节点

struct node{
    int sum, tag; // 常规都区间和 & 标记
    int len; 也很好理解
    
    // 然后就有些奇怪都东西了
    int len_2, len_sum, con;
};

con: contribution, 即为该节点对答案分子的贡献，$con_rt = \sum sum_i^2$

因为con比较难以一步计算出来，所以考虑一个比较容易想到(放屁)的区间平方和

$sum^2$更新时，$sum_{new}^2 = (sum_{old} + tag * len)^2 = sum_{old}^2 + 2*len * tag * sum_{old} + len^2 * tag^2$

即 sum += $2*len*tag*sum_{old} + len^2*tag^2$

包含上子节点的话就是，$\sum sum^2$，也就是 con 了

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ con & += \…

对于难以统计的 $\sum ((len*sum))$ 和 $\sum (len^2 )$ 这里变可以单独维护，这里便是Node结构体里奇怪的len_sum, len_2，注释里标注了include child nodes，都是包含其子节点的。

那么考虑这两个奇怪的东西，

• $\sum (len_i^2 )$简单，建树的时候直接构造就好了
• 对于$\sum (len_i*sum_i)$
• $ \begin{align*}
  \sum (len_isum_i)_{new} & = \sum(len_i * (sum_i + len_itag)) \
  &= \sum(len_i * sum_i + len_i^2tag) \
  &= \sum(len_isum_i)_{old} + tag * \sum len_i^2
  \end{align*} $

又回到了len_2

所以这里代码里对应的：

• len_2: $\sum len_i^2$
• len_sum: $\sum(len_i*sum_i)$
• con: $\sum sum^2$,答案的分子在con[root]里

这么一来，线段树部分就很清晰了，自认为自己的数学功底很差，所以推公式的时候慢慢推，让像我一样的弱智都能看得懂

本来想交一发 long long先来个90分的，然后发现，前90分也要__int128，这便是这题毒瘤的地方了。代码量到这里已经可以了，何必再爆long long,数据结构配高精有意思吗？有意思吗？有意思吗？据观察大家都用的__int128过的。

不过听郭黑康说最后一个点q是MOD的倍数（题目不是保证不是倍数的吗？？？），没遇到这个坑，也不知道是不是我写法的原因，int128之后CE了几发就过了

最后输出答案的时候，gcd,power啥的，就不说了，老生常谈了

#include <bits/stdc++.h>
using namespace std;
typedef __int128 LL;
const int N = (1e5 + 7) << 2;
const LL MOD = 998244353;

LL sqr(LL x){return x*x;}
LL gcd(LL x, LL y){
	if (y) while((x %= y) && (y %= x));
	return x + y;
}
LL power(LL a, LL x){
    LL ans = 1;
    for (; x; x >>= 1){
        if (x & 1) ans = (ans * a) % MOD;
        a = (a * a) % MOD;
    }
    return ans % MOD;
}
//------------head & math-------------

int arr[N];

struct SegTree{
    #define lc (rt << 1)
    #define rc (rt << 1 | 1)
    #define lson rt<<1, l, mid
    #define rson rt<<1|1, mid+1, r

    int n;
    // for one Node
    LL sum[N], len[N], tag[N];
    LL len_2[N], len_sum[N];  // include child nodes
    LL con[N]; // contribution, also include child nodes

    // commonly pushUp
    void pushUp(const LL &rt) {
        sum[rt] = sum[lc] + sum[rc];
        len_sum[rt] = len[rt]*sum[rt] + len_sum[lc] + len_sum[rc];
        con[rt] = sqr(sum[rt]) + con[lc] + con[rc];
    }

    void Tag(const LL &rt, const LL &l, const LL &r, const LL &v){
        sum[rt] += v * (r-l+1);
        tag[rt] += v;
        con[rt] += 2*v*len_sum[rt] + sqr(v)*len_2[rt];
        len_sum[rt] += v * len_2[rt];
    }

    void pushDown(const LL &rt, const LL &l, const LL &r){
        if (!tag[rt]) return;
        LL mid = (l+r) >> 1;
        Tag(lson, tag[rt]);
        Tag(rson, tag[rt]);
        tag[rt] = 0;
    }

    void build(const LL &rt, const LL &l, const LL &r) {
        if (l == r) {
            sum[rt] = len_sum[rt] = (LL)arr[l];
            len[rt] = len_2[rt] = 1;
            tag[rt] = 0;
            con[rt] = sqr(sum[rt]);
            return;
        }
        LL mid = (l + r) >> 1;
        build(lson);
        build(rson);
        len[rt] = len[lc] + len[rc];
        len_2[rt] = sqr(len[rt]) + len_2[lc] + len_2[rc];
        tag[rt] = 0;
        pushUp(rt);
    }

    void update(const LL &rt, const LL &l, const LL &r, const LL &L, const LL &R, const LL &v) {
        if (L <= l && r <= R) {
            Tag(rt, l, r, v);
            return;
        }
        LL mid = (l + r) >> 1;
        pushDown(rt, l, r);
        if (L <= mid) update(lson, L, R, v);
        if (mid <  R) update(rson, L, R, v);
        pushUp(rt);
    }

    void query(){ // print ans;
        LL p = con[1], q = sum[1], gd = gcd(p, q);
        p /= gd, q /= gd;
        //printf("%d, %d: ", p, q);
        LL ans = ((p%MOD) * power(q, MOD-2)) % MOD;
        printf("%lld\n", ans);
    }

    void print(LL rt, LL l, LL r){ // prLL tree, debug
        printf("%d: [%d, %d], len = %d, len_2 = %d, sum = %d, len_sum = %d, tag = %d, con = %d\n", 
            rt, l, r, len[rt], len_2[rt], sum[rt], len_sum[rt], tag[rt], con[rt]);
        if (l == r) return;
        LL mid = (l + r) >> 1;
        print(rt<<1, l, mid);
        print(rt<<1|1, mid+1, r);
    }
} T;


int main(){
    //freopen("in.txt", "r", stdin);
    int n, m;
    scanf("%d%d", &n, &m);
    for (LL i = 1; i <= n; i++){
        scanf("%d", &arr[i]);
    }
    T.build(1, 1, n);
    //T.print(1, 1, n);

    for (int op, l, r, v; m--;){
        scanf("%d", &op);
        if (op==2) T.query();
        else{ // update
            scanf("%d%d%d", &l, &r, &v);
            T.update(1, 1, n, l, r, v);
        }
    }
    return 0;
}

最后再扯点啥呢，自己写结构体都是把结构体当成class来用的，就当是全是public的class吧

define lson, rson也是一个令人愉悦的点，跟kuangbing学的

还有哪里看不懂欢迎私戳我提问或者cww970329@qq.com

附件：

• 可能炸的公式1

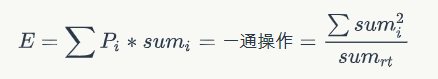
• 可能炸的公式1

• 可能炸的公式2