排序算法—快速排序（Quick Sort）

快速排序（Quick Sort）

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

1.算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 “基准”（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。/

2.具体算法实现

• 先选择一个基准（base），一般是数组最左边的值，或者是最右边的值（如果base是左边，则从右边开始。）

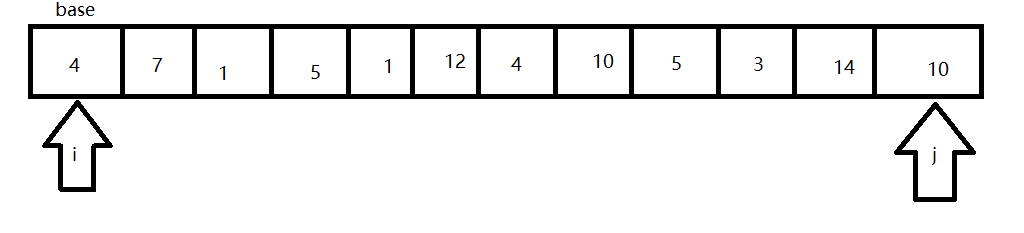
• 如果j需要从右往左遍历，如果发现arr[j]<base则停下，i开始从左往右遍历，发现arr[i]>base停下。
  
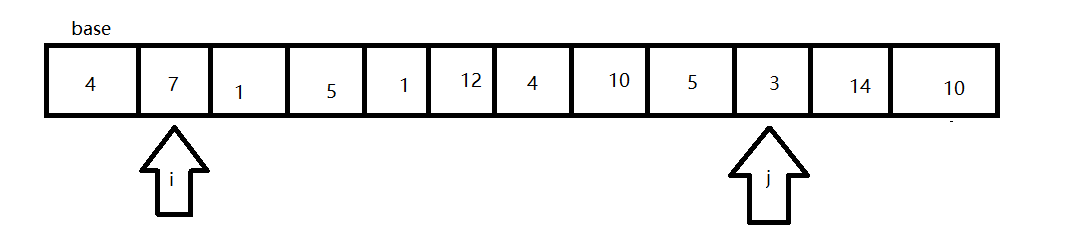
• 交换arr[i]与arr[j]的位置
  
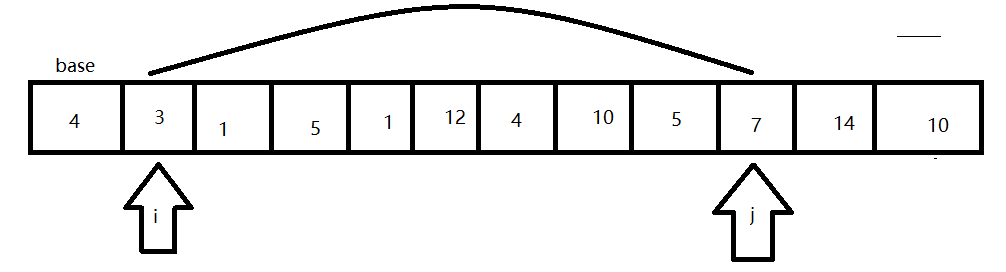
• 然后j和i继续寻找，并交换位置
  
  
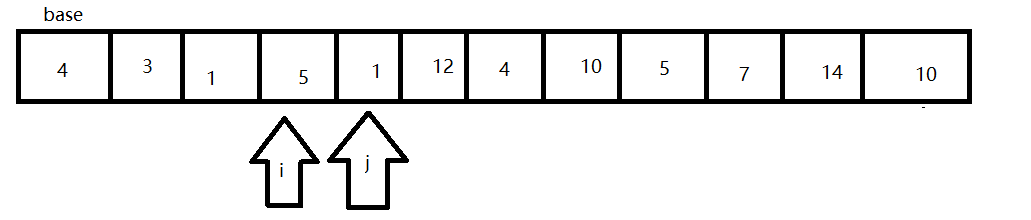
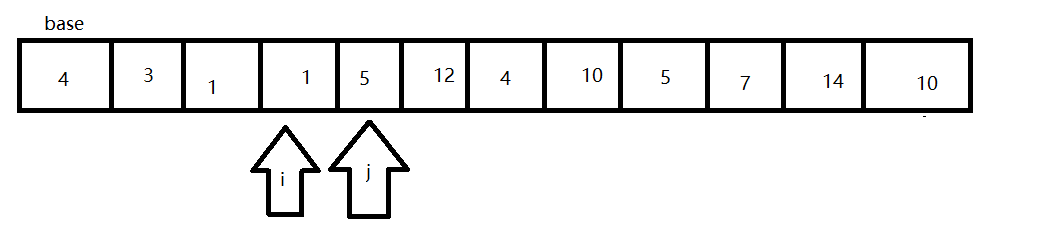
• 当i和j相同时，结束一轮寻找，并将此时的数字与base交换。
  
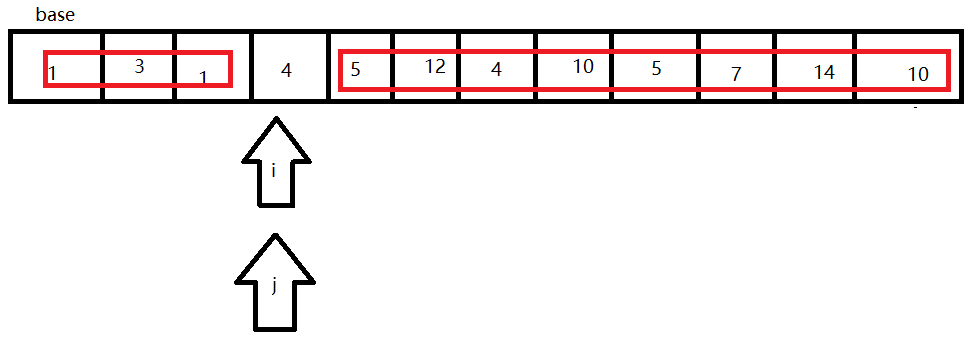
• 此时根据base，将数组分割成两个部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

3. 算法分析

快速排序算法的时间复杂度和各次标准数据元素的值关系很大。如果每次选取的标准元素都能均分两个子数组的长度,这样的快速排序过程是一个完全二叉树结构。(即每个结点都把当前数组分成两个大小相等的数组结点,n个元素数组的根结点的分解次数就构成一棵完全二叉树)。这时分解次数等于完全二叉树的深度log2n;每次快速排序过程无论把数组怎样划分、全部的比较次数都接近于n-1次，所以最好情况下快速排序算法的时间复杂度为O(nlog2n):快速排序算法的最坏情况是数据元素已全部有序，此时数据元素数组的根结点的分需次数构成一棵二叉退化树(即单分支二叉树),一棵二叉退化树的深度是n,所以最坏情况下快速排序算法的时间复杂度为O(n2)。般情况下 ,标准元素值的分布是随机的，数组的分邮大数构成模二又树，这样的二叉树的深度接近于log2n, 所以快速排序算法的平均(或称期望）时间复杂度为O(nlog2n)

public class quickSort {
    public static  void  main(String[] args)
    {
        int[] arr=new int[10000];
        int n=arr.length;
        Random random = new Random();//默认构造方法
        for(int i=0;i<n;i++)
        {
            arr[i]=(int)random.nextInt(100);//在数组中随机生成[0，100)的数
        }
        funQuickSort(arr,0,n-1);

    }

    public static  void funQuickSort(int[] arr,int start,int end )
    {
        if(start>end)
        {
            return;
        }
        int base=arr[start];
        int i=start;
        int j=end;
        while (i!=j)
        {
            while(arr[j] >= base && i < j)
            {
                j--;
            }
            while(arr[i] <= base && i < j)
            {
                i++;
            }
            int temp=arr[i];
            arr[i]=arr[j];
            arr[j]=temp;
        }
        arr[start]=arr[i];
        arr[i]=base;
        funQuickSort(arr,start,i-1);
        funQuickSort(arr,j+1,end);
    }
}

快速排序前的数组：2 43 7 46 43 25 26 36 22 35 32 41 26 34 42 29 39 43 4 3 46 4 17 45 36 48 21 16 26 0 39 45
快速排序后的数组：0 2 3 4 4 7 16 17 21 22 25 26 26 26 29 32 34 35 36 36 39 39 41 42 43 43 43 45 45 46 46 48