二维几何前置知识

前言:只写了部分的前置知识

精度问题

计算几何的坐标一般是实数，会出现精度问题，所以我们每次运算时需要设一个精度偏差值\(eps\)，一般取1e^-8

const double eps=1e-8;

一般浮点数用\(double\)

判断正负

int sgn(double x){
	if(fabs(x)<eps) return 0;
	if(x<0) return -1;
	return 1;
}

比较大小

int dcmp(double x,double y){
	if(fabs(x-y)<eps) return 0;
	if(x<y) return -1;
	return 1;
}

点\((Point)\)

定义

struct Point{
	double x,y;
	Point(){}
	Point(double x,double y):x(x),y(y){}
};

两点之间距离

double Dis(Point A,Point B){
	return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
}

向量\((vector)\)

定义

向量指具有大小和方向的量。它可以形象化地表示为带箭头的线段。
箭头所指：代表向量的方向；线段长度：代表向量的大小

表示

由于向量只与大小和方向有关，我们可以把向量看成原点\((0,0)\)到一个点\((x,y)\)的有向线段,直接用点的数据结构来表示向量

#define Point Vector

向量的运算

加

点与向量相加得到另一个点，向量与向量相加得到另外一个向量

Point operator +(Point B){return Point(x+B.x,y+B.y);}

减

两个点的差是一个向量，向量\(A\)减\(B\)得到由\(B\)指向\(A\)的向量

Point operator -(Point B){return Point(x-B.x,y-B.y);}

乘

向量与实数相乘得到等比例放大的向量

Point operator *(double k){return Point(x*k,y*k);}

除

向量与实数相除得到等比例缩小的向量

Point operator /(double k){return Point(x/k,y/k);}

相等

bool operator ==(Point B){return sgn(x-B.x)==0&&sgn(y-B.x)==0;}

叉积\((cross product)\)

计算公式:
\(C=A*B=|A||B|sin<a,b> \)

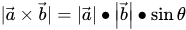
double Cross(Vector A,Vector B){
	return A.x*B.y-A.y*B.x;
}

可用于:算两个向量所构成的平行四边形面积,判断两个向量的方向等等

Wating to end...