树状数组学习笔记

众所周知，树状数组是一个常用的数据结构。。。

1.为啥用树状数组：

如果用普通的前缀数组来维护前缀的信息，即使查询时o(1)的，但是修改就几乎要o(n)，效率有时十分低下.

而树状数组却弥补了这一缺点，修改和查询都是o(logn)的

2.如何构建树状数组：

根据二次幂的性质，我们可以把一个数转化成一个独一无二的二进制数，所以，我们可以建立一个类似于二进制数的数组来维护前缀和

假如一个整数　　x可以别分为x=2^i1+2^i2+2^i3...+2^im那么就可以把一个区间[1...x]分为(logx)的几个小区间

假设i1>i2>i3>...im

1长度为2^i1区间[1,2^i1]

2长度为2^i2区间[2^i1+1,2^i1+2^i2]

3长度为2^i3区间[2^i2+2^i1+1,2^i1+2^i2+2^i3]

...

这些小区间的特点是长度为二进制分解下最小的二次幂，也就是lowbit(x);

 例如11=8+2+1=2^3+2^1+2^0,那么区间11可以分为[1,8],[9,10],[11],长度分别为lowbit(8)=8,lowbit(10)=2,lowbit(11)=1

 

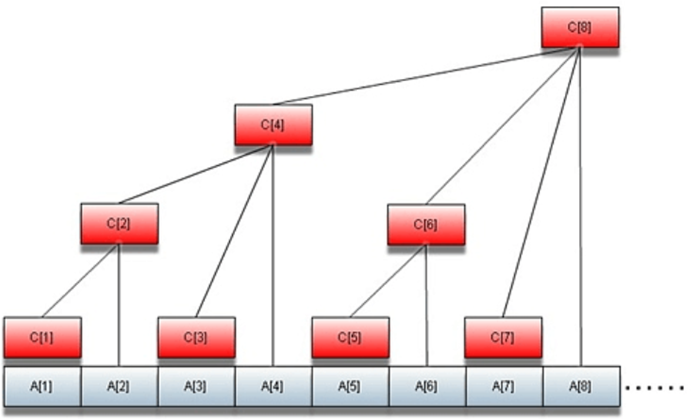
 C[i]=A[i]+A[i-1]+A]i-lowbit(i)+1]

C[1] = A[1];

C[2] = A[1] + A[2];

C[3] = A[3];

C[4] = A[1] + A[2] + A[3] + A[4];

C[5] = A[5];

C[6] = A[5] + A[6];

C[7] = A[7];

C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

求lowbit(i):

lowbit(i)=i&(-i);

修改

void insert(long long x,long long vol) {
    while(x<=n) {
        c[x]+=vol;
        x+=lowbit(x);
    }
}

查询

long long ask(long long x) {
    long long sum=0;
    while(x) {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}

特别注意，树状数组的下标不能为0，比如insert(0,a)和ask(0)

模板题https://www.luogu.com.cn/problem/P3374

话不多说，直接上代码

#include<bits/stdc++.h>
using namespace std;
long long lowbit(long long x) {
    return x&(-x);
}
long long n,m,c[1000000],a[1000000];
void insert(long long x,long long vol) {
    while(x<=n) {
        c[x]+=vol;
        x+=lowbit(x);
    }
}
long long ask(long long x) {
    long long sum=0;
    while(x) {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}

int main() {
    scanf("%lld%lld",&n,&m);
    for(long long i=1; i<=n; i++) {
        scanf("%lld",&a[i]);
        insert(i,a[i]);
    }

    for(long long i=1; i<=m; i++) {
        long long x,y,s;
        scanf("%lld%lld%lld",&s,&x,&y);
        if(s==1) insert(x,y);
        else {
            long long p=ask(y)-ask(x-1);
            printf("%lld\n",p);
        }
    }

}

 

 例题：https://www.luogu.com.cn/problem/P1428

 第一眼看到题目，就想到了暴力，发现就是求维护一个小于第i头鱼的可爱值的前缀，但如果数据范围大一些呢？

仔细分析，这里我们就需要运用到树状数组

样例：

6
4 3 0 5 1 2
我们可以把每一个小鱼的权值当作当作树状数组的序号，把它的权值加上一，就相当于等于这个权值的小鱼多了一个，我们只需要找出小于这个权值的数目就行了

#include<bits/stdc++.h>
using namespace std;
const int N=100001;
int c[N],n,ans,b[N];
int lowbit(int x)
{
    return x&(-x);
}
struct data{
    int x,y;
}a[N];
bool cmp(data c,data d){
    if(c.x==d.x) return c.y<d.y;
    return c.x<d.x;
}
void insert(int x)
{
    while(x<=N)
    {
        c[x]++;//为什么是加1呢就相当于是把等于这个权值的小鱼加1 
        x+=lowbit(x);
    }
}
int ask(int x)
{
    long long sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d",&x);
            cout<<ask(x)<<" ";//找出比x小的有多少 
        insert(x+1);//因为是统计小于这个数的，所以要加1，请仔细思考 
    }

}

如果数据太大，要用离散化

#include<bits/stdc++.h>
using namespace std;
const int N=100001;
int c[N],n,ans,b[N];
int lowbit(int x)
{
    return x&(-x);
}
struct data{
    int x,y;
}a[N];
bool cmp(data c,data d){
    if(c.x==d.x) return c.y>d.y; //这样可以保证严格小于的情况 
    return c.x<d.x;
}
void insert(int x)
{
    while(x<=n)
    {
        c[x]++;
        x+=lowbit(x);
    }
}
int ask(int x)
{
    long long sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
int main(){
    scanf("%d",&n);
    a[0].x=-1;
    for(int i=1;i<=n;i++){
       scanf("%d",&a[i].x);
       a[i].y=i;//记录第i个数的坐标，因为在排序后会被打乱 
    }
    sort(a+1,a+n+1,cmp);
    int tot=1;
    for(int i=1;i<=n;i++){    
    b[a[i].y]=i; //a[i].y相当于第i小的数的坐标，把这个坐标设为第i小 
}

    for(int i=1;i<=n;i++){
    cout<<ask(b[i])<<" ";//b[i]相当于第i个数是第几大的 
        insert(b[i]);
    }
}

但由于要排序，所以这个代码不快

例题2：http://bzoj.org/p/1016

首先，可以写dp

转移方程轻易得出

设s[i]是前i个数的前缀

f[i]+=f[j](s[j]>s[i])

#include<bits/stdc++.h>
using namespace std;
const long long N=5*1e5;
const long long mod=1000000009;
long long s[N],ans,n,a[N],f[N];
int main(){
    scanf("%lld",&n);
    for(long long i=1;i<=n;i++)
    scanf("%lld",&a[i]),s[i]=s[i-1]+a[i];
    f[0]=1;
    for(int i=1;i<=n;i++)
    for(int j=0;j<i;j++)
    {
        if(s[i]>=s[j])
        f[i]=(f[i]+f[j])%mod;
    }
        cout<<f[n];
}

 这一段其实可以用树状数组来优化

只需要找到前面有多少比他小

f[0]=1,所以当s[i]<0，那么这种情况就不可取，所以也要把0打入树状数组

#include<bits/stdc++.h>
using namespace std;
const long long N=1e6+10,mod=1000000009;
long long n,c[N],aa[N],ans;
struct data{
    long long num,vol;
}a[N];
bool cmp(data c,data d){
    if(c.vol==d.vol) return c.num<d.num;
    else return c.vol<d.vol;
}
long long lowbit(long long x){
    return x&(-x);
}
void insert(long long x,long long vol){
    while(x<=N){
        c[x]=(c[x]+vol)%mod;
        x+=lowbit(x);
        
    }
}
long long ask(long long x){
    long long sum=0;
    while(x){
        sum=(sum+c[x])%mod;
        x-=lowbit(x);
    }
    return sum;
}
int main(){
    scanf("%lld",&n);    
    for(long long i=1;i<=n;i++)
    {
        long long x;
        scanf("%lld",&x);
        a[i].vol=a[i-1].vol+x;//算出前缀    
        a[i].num=i;    //标记位置，日常离散化 
    }
    sort(a+1,a+n+1,cmp);
    long long falg=0;//falg统计有多少个前缀比0小 (falg比flag好打，篡改单词) 
    for(int i=1;i<=n;i++){
    if(a[i].vol<0) falg++; 
}
    falg++;//falg统计有多少个前缀比0小 ,所以0应该是第falg+1小 
    long long tot=0,i=0;//tot表示运行了多少次，应该要运行n+1次，因为还要包括0，i表示第i小的数 
    while(tot<=n+1){
    
    if(tot==falg) insert(falg,1);//为什么这里i不++呢，因为没有跳到下一个值,insert(falg,1)相当于把0放入树状数组，因为0是第flag小的 
    else aa[a[i].num]=tot,i++;
    tot++;
}//日常离散化  

    for(long long i=1;i<=n;i++)
    {  
       long long f=ask(aa[i]);
       if(i==n) cout<<f;//输出f[n] 
       insert(aa[i],f);
    }

}

树状数组虽然快但是也有局限性，维护的东西特别少，不宜拓展

谢谢阅读

//黄鸡djskal爆蔡我