自然语言第四课（HMM）

Hidden Markov Model（HMM）

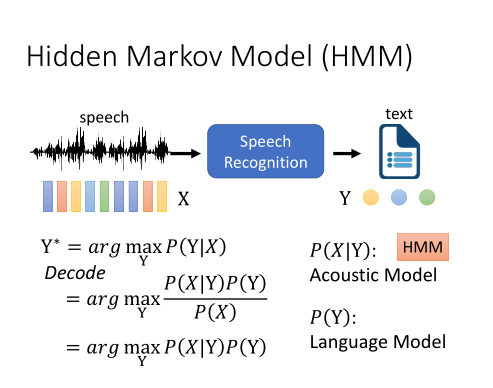
　　X是输入语音序列，Y是输出文字，我们的目标是穷举所有可能的Y，找到一个P(Y|X)最大化。这个过程叫作解码。
　　根据贝叶斯定律，我们可以把它变成P(X|Y)P(Y)/P(X)。
　　由于P(X)与我们的解码任务是无关的，因为不会随着Y变化而变化，所以我们只需要算argmaxP(X|Y)P(Y)。
　　前面这项P(X|Y)是Acoustic Model，HMM可以建模，后面那项P(Y)是Language Model，有很多种建模方式。

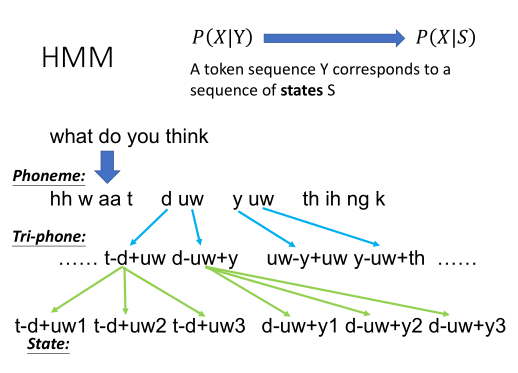
　　音标、字或词，这些单位，对HMM的隐变量来说，都太大了。所以我们需要为P(X|Y)建模，变成为P(X|S)建模。S为状态，是人定义的。它是比音素Phoneme还要小的单位。
　　序列中的每一个音素，都会受到前后音素单位的影响。我们会用一个Tri-phone，把当前的每一个音素，都加上它前后的音素，相当于把原来的音素切得更细。
　　这样d后面的uw，和y后面的uw表达出来就会是不同的单位了。

　　

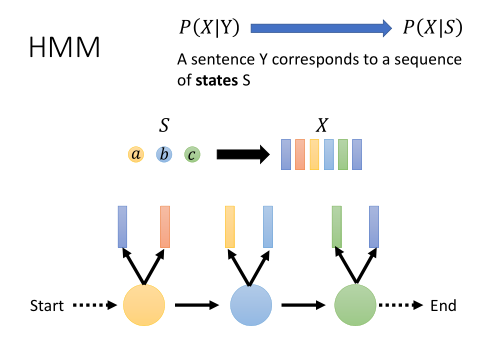
 　　假设我们有一段声音信号X，它内容包含了一系列特征向量。我们会先从Start状态转移到第一个状态，发射出一些向量，再到第二个状态，发射出一些向量……以此类推，直至走到END状态。

　　在HMM中如何使用深度学习

　　　　方法1：Tandem（串联）

　　　　　　之前的声学特征是MFCC格式，深度学习方法输入一个MFCC，预测它属于哪个状态的概率。
　　　　　　接着我们把HMM的输入，原为声学特征，由深度学习的输出取代掉。我们也可以取最后一个隐层或者是瓶颈层(bottleneck)。

　　　　方法2：DNN-HMM Hybrid（混合模型）

　　　　　　HMM中有一个高斯混合模型。我们想把它用DNN取代掉。
　　　　　　高斯混合模型是给定一个状态，预测声学特征向量的分布，即P(x|a)。
　　　　　　而DNN是训练一个State的分类器，计算给定一个声学特征下，它是某个状态的概率，即P(a|x)。
　　　　　　用贝叶斯定律，可以得到P(x|a)=P(a|x)P(x)/P(a)。
　　　　　　P(a)可以通过在训练资料中统计得到。P(x)可以忽略。

　　https://www.cnblogs.com/yanqiang/p/13268037.html