AES算法实现与优化
AES算法实现与优化
AES算法简介
高级加密标准(英语:Advanced Encryption Standard,缩写:AES),又称Rijndael加密法(荷兰语发音: [ˈrɛindaːl],音似英文的“Rhine doll”),是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES,已经被多方分析且广为全世界所使用。经过五年的甄选流程,高级加密标准由美国国家标准与技术研究院(NIST)于2001年11月26日发布于FIPS PUB 197,并在2002年5月26日成为有效的标准。现在,高级加密标准已然成为对称密钥加密中最流行的算法之一。
该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计,结合两位作者的名字,以Rijndael为名投稿高级加密标准的甄选流程。
| 密钥长度 | 128、192、156bit |
|---|---|
| 分组长度 | 128bit |
| 结构 | 置换排列网络 |
| 重复回数 | 10、12、14等(视密钥长度而定) |
关系密码攻击可以破解9个加密循环/256比特(密钥)的AES。另外选择明文攻击可以破解8个加密循环,192或256比特(密钥)的AES,或7个加密循环、128位(密钥)的AES。
密码说明
严格地说,AES和Rijndael加密法并不完全一样(虽然在实际应用中两者可以互换),因为Rijndael加密法可以支持更大范围的区块和密钥长度:AES的区块长度固定为128比特,密钥长度则可以是128,192或256比特;而Rijndael使用的密钥和区块长度均可以是128,192或256比特。加密过程中使用的密钥是由Rijndael密钥生成方案产生。
大多数AES计算是在一个特别的有限域完成的。
AES加密过程是在一个4×4的字节矩阵上运作,这个矩阵又称为“体(state)”,其初值就是一个明文区块(矩阵中一个元素大小就是明文区块中的一个Byte)。(Rijndael加密法因支持更大的区块,其矩阵的“列数(Row number)”可视情况增加)加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:
AddRoundKey—矩阵中的每一个字节都与该次轮密钥(round key)做XOR运算;每个子密钥由密钥生成方案产生。SubBytes—透过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。ShiftRows—将矩阵中的每个横列进行循环式移位。MixColumns—为了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每内联的四个字节。最后一个加密循环中省略MixColumns步骤,而以另一个AddRoundKey取代。
代码流程图如下图:
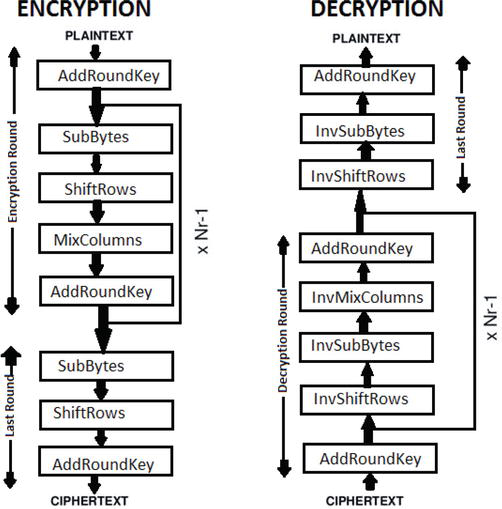
对应的c语言代码如下:
static void Cipher(state_t* state, const uint8_t* RoundKey)
{
uint8_t round = 0;
AddRoundKey(0, state, RoundKey);
for (round = 1; ; ++round) {
SubBytes(state);
ShiftRows(state);
if (round == Nr) {
break;
}
MixColumns(state);
AddRoundKey(round, state, RoundKey);
}
AddRoundKey(Nr, state, RoundKey);
}
解谜操作与加密操作相反,
AddRoundKey步骤
AddRoundKey步骤,回合密钥将会与原矩阵合并。在每次的加密循环中,都会由主密钥产生一把回合密钥(通过Rijndael密钥生成方案产生),密钥大小会跟原矩阵一样,与原矩阵中每个对应的字节作XOR操作。
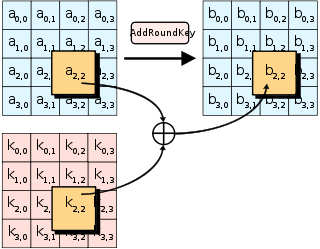
对应的c代码如下:
static void AddRoundKey(uint8_t round, state_t* state, const uint8_t* RoundKey) {
uint8_t i,j;
for (i = 0; i < 4; ++i) {
for (j = 0; j < 4; ++j) {
(*state)[i][j] ^= RoundKey[(round * Nb * 4) + (i * Nb) + j];
}
}
}
SubBytes步骤
在SubBytes步骤中,矩阵中的各字节通过一个8位的 S-box 进行转换。这个步骤提供了加密法非线性的变换能力。S-box 与 $GF(2^8)$ 上的乘法逆元有关,已知具有良好的非线性特性。为了避免简单代数性质的攻击,S-box结合了乘法逆元及一个可逆的仿射变换矩阵建构而成。此外在建构S-box时,刻意避开了不动点与反不动点,即以S-box替换字节的结果会相当于错排的结果。
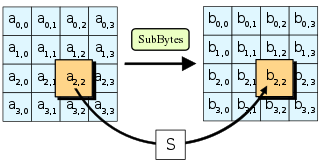
对应的c代码:
static void SubBytes(state_t* state) {
uint8_t i, j;
for (i = 0; i < 4; ++i) {
for (j = 0; j < 4; ++j) {
(*state)[j][i] = getSBoxValue((*state)[j][i]);
}
}
}
AES算法的 S-box:
static const uint8_t sbox[256] = {
//0 1 2 3 4 5 6 7 8 9 A B C D E F
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 };
ShiftRows步骤
ShiftRows描述矩阵的列操作。在此步骤中,每一列都向左循环位移某个偏移量。在AES中(区块大小128位),第一列维持不变,第二列里的每个字节都向左循环移动一格。同理,第三列及第四列向左循环位移的偏移量就分别是2和3。128位和192比特的区块在此步骤的循环位移的模式相同。经过ShiftRows之后,矩阵中每一竖行,都是由输入矩阵中的每个不同行中的元素组成。Rijndael算法的版本中,偏移量和AES有少许不同;对于长度256比特的区块,第一列仍然维持不变,第二列、第三列、第四列的偏移量分别是1字节、2字节、3字节。除此之外,ShiftRows操作步骤在Rijndael和AES中完全相同。
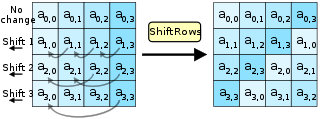
对应的c代码:
static void ShiftRows(state_t* state) {
uint8_t temp;
// Rotate first row 1 columns to left
temp = (*state)[0][1];
(*state)[0][1] = (*state)[1][1];
(*state)[1][1] = (*state)[2][1];
(*state)[2][1] = (*state)[3][1];
(*state)[3][1] = temp;
// Rotate second row 2 columns to left
temp = (*state)[0][2];
(*state)[0][2] = (*state)[2][2];
(*state)[2][2] = temp;
temp = (*state)[1][2];
(*state)[1][2] = (*state)[3][2];
(*state)[3][2] = temp;
// Rotate third row 3 columns to left
temp = (*state)[0][3];
(*state)[0][3] = (*state)[3][3];
(*state)[3][3] = (*state)[2][3];
(*state)[2][3] = (*state)[1][3];
(*state)[1][3] = temp;
}
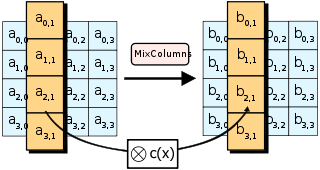
MixColumns步骤
在MixColumns步骤,每一列的四个字节通过线性变换互相结合。每一列的四个元素分别当作${\displaystyle 1,x,x{2},x{3}}$ 的系数,合并即为 ${\displaystyle GF(2^{8})}$ 中的一个多项式,接着将此多项式和一个固定的多项式 ${\displaystyle c(x)=3x{3}+x+x+2}$ 在模 ${\displaystyle x^{4}+1}$ 下相乘。此步骤亦可视为Rijndael有限域之下的矩阵乘法。MixColumns函数接受4个字节的输入,输出4个字节,每一个输入的字节都会对输出的四个字节造成影响。因此ShiftRows和MixColumns两步骤为这个密码系统提供了扩散性。
对应c代码:
static uint8_t xtime(uint8_t x)
{
return ((x<<1) ^ (((x>>7) & 1) * 0x1b));
}
// MixColumns function mixes the columns of the state matrix
static void MixColumns(state_t* state)
{
uint8_t i;
uint8_t Tmp, Tm, t;
for (i = 0; i < 4; ++i) {
t = (*state)[i][0];
Tmp = (*state)[i][0] ^ (*state)[i][1] ^ (*state)[i][2] ^ (*state)[i][3] ;
Tm = (*state)[i][0] ^ (*state)[i][1] ; Tm = xtime(Tm); (*state)[i][0] ^= Tm ^ Tmp ;
Tm = (*state)[i][1] ^ (*state)[i][2] ; Tm = xtime(Tm); (*state)[i][1] ^= Tm ^ Tmp ;
Tm = (*state)[i][2] ^ (*state)[i][3] ; Tm = xtime(Tm); (*state)[i][2] ^= Tm ^ Tmp ;
Tm = (*state)[i][3] ^ t ; Tm = xtime(Tm); (*state)[i][3] ^= Tm ^ Tmp ;
}
}
密码算法实现
Rijndael的作者曾经为该算法提供了一个[主页](IAIK Krypto Group - AES Lounge (archive.org))。
现在这个主页的内容已经扩充了许多内容:
包括一些分析AES安全性的论文、AES硬件实现、高速AES实现、低代价AES实现、软件实现、侧信道分析、出错分析、AES扩展指令集等等内容。
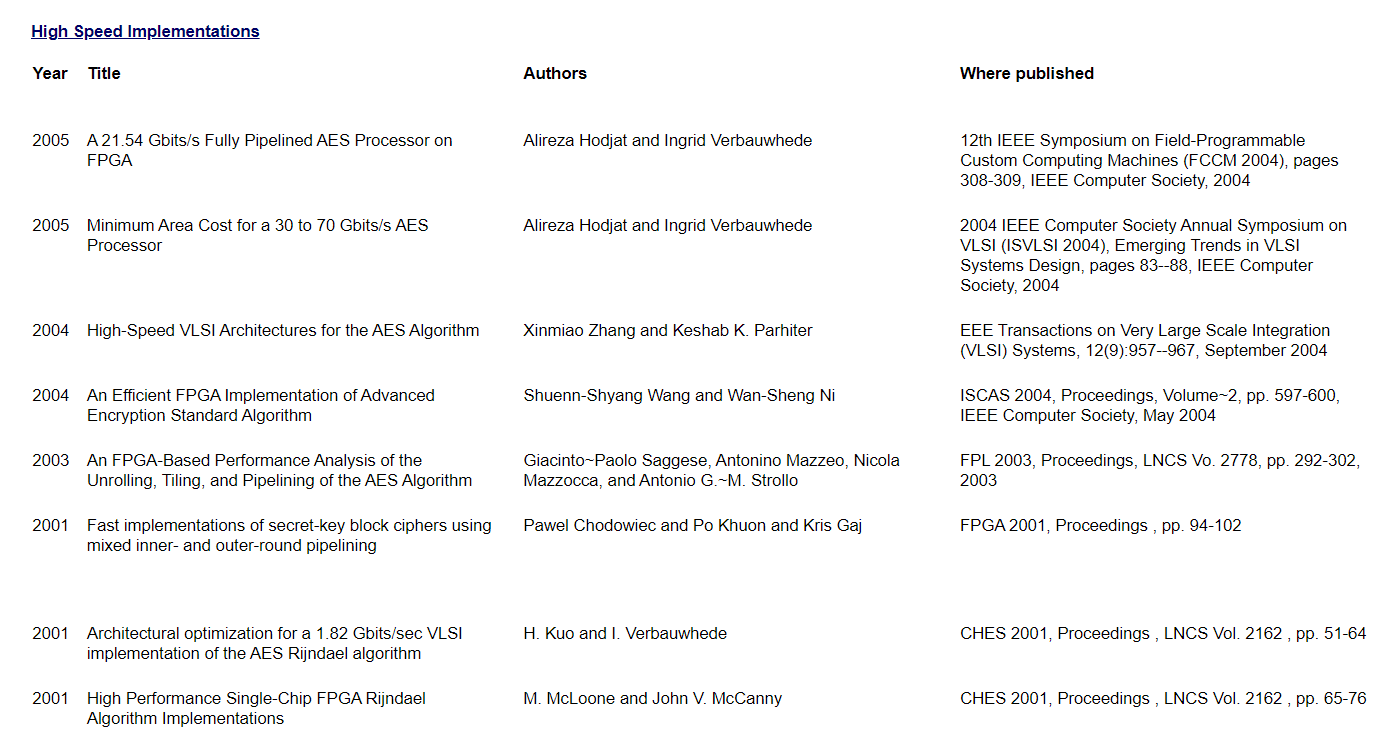
可以看到AES加密速率从2001年的1.82Gbits/sec发展到2005年21.54Gbits/sec以及70Gbits/sec,发展非常迅速,大多都是使用FPGA在硬件算法实现层面进行的优化。

在侧信道分析部分可以看到经典的论文,比如AES高阶掩码,功率分析等等。有机会可以看一看。
在软件中实现AES时应该小心,特别是围绕侧通道攻击。
对较短的块进行加密只能通过填充源字节(通常使用空字节)来实现。
算法实现需要考虑的细节
分组密码有五种工作体制:
- 电码本模式(Electronic Codebook Book (ECB));
- 2.密码分组链接模式(Cipher Block Chaining (CBC));
- 计算器模式(Counter (CTR));
- 密码反馈模式(Cipher FeedBack (CFB));
- 输出反馈模式(Output FeedBack (OFB))
电码本模式(Electronic Codebook Book (ECB)
这种模式是将整个明文分成若干段相同的小段,然后对每一小段进行加密。
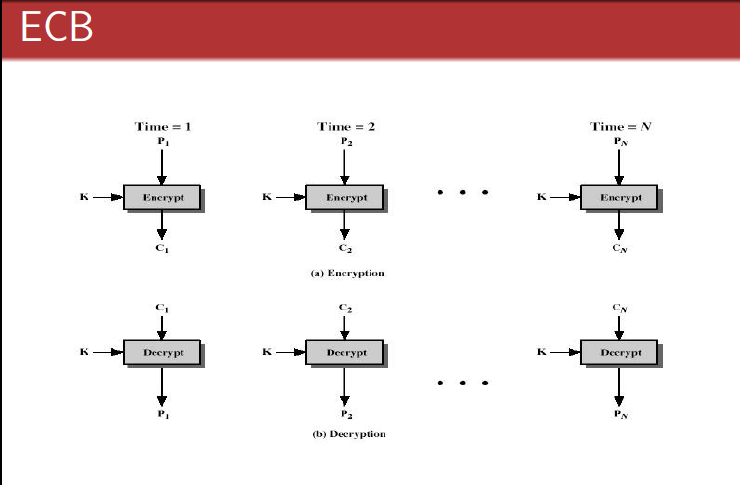
这个方法很简单,但是不安全,因为保留了明文的结构信息。
对应的c代码实现:
void AES_ECB_encrypt(const struct AES_ctx* ctx, uint8_t* buf)
{
Cipher((state_t*)buf, ctx->RoundKey);
}
void AES_ECB_decrypt(const struct AES_ctx* ctx, uint8_t* buf)
{
InvCipher((state_t*)buf, ctx->RoundKey);
}
密码分组链接模式(Cipher Block Chaining (CBC))
这种模式是先将明文切分成若干小段,然后每一小段与初始块或者上一段的密文段进行异或运算后,再与密钥进行加密。
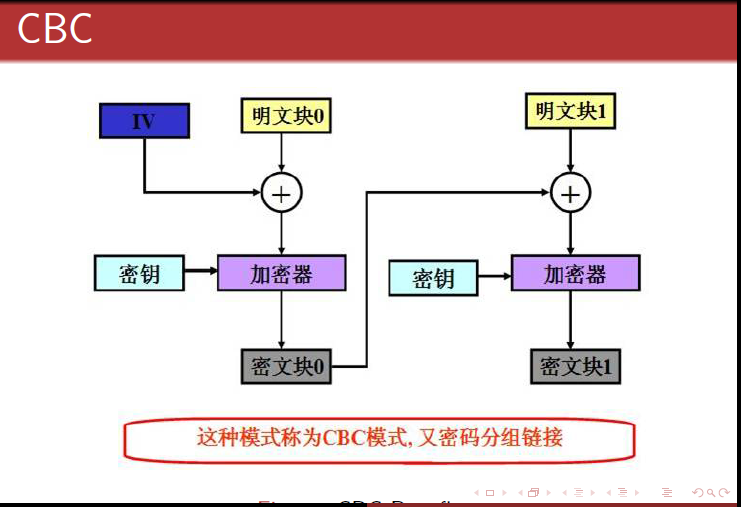
对应c实现:
static void XorWithIv(uint8_t* buf, const uint8_t* Iv)
{
uint8_t i;
for (i = 0; i < AES_BLOCKLEN; ++i) {
buf[i] ^= Iv[i];
}
}
void AES_CBC_encrypt_buffer(struct AES_ctx *ctx, uint8_t* buf, size_t length)
{
size_t i;
uint8_t *Iv = ctx->Iv;
for (i = 0; i < length; i += AES_BLOCKLEN) {
XorWithIv(buf, Iv);
Cipher((state_t*)buf, ctx->RoundKey);
Iv = buf;
buf += AES_BLOCKLEN;
}
memcpy(ctx->Iv, Iv, AES_BLOCKLEN);
}
void AES_CBC_decrypt_buffer(struct AES_ctx* ctx, uint8_t* buf, size_t length)
{
size_t i;
uint8_t storeNextIv[AES_BLOCKLEN];
for (i = 0; i < length; i += AES_BLOCKLEN) {
memcpy(storeNextIv, buf, AES_BLOCKLEN);
InvCipher((state_t*)buf, ctx->RoundKey);
XorWithIv(buf, ctx->Iv);
memcpy(ctx->Iv, storeNextIv, AES_BLOCKLEN);
buf += AES_BLOCKLEN;
}
}
计算器模式(Counter CTR)
计算器模式不常见,在CTR模式中, 有一个自增的算子,这个算子用密钥加密之后的输出和明文异或的结果得到密文,相当于一次一密。这种加密方式简单快速,安全可靠,而且可以并行加密,但是在计算器不能维持很长的情况下,密钥只能使用一次。CTR的示意图如下所示:
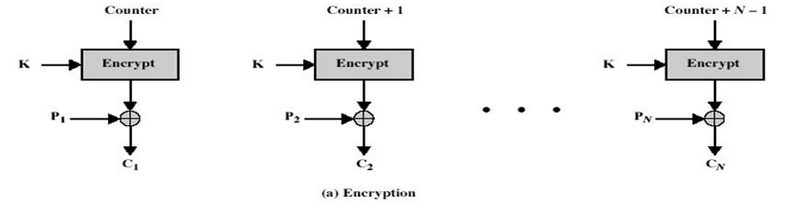
对应的c代码:
void AES_CTR_xcrypt_buffer(struct AES_ctx* ctx, uint8_t* buf, size_t length)
{
uint8_t buffer[AES_BLOCKLEN];
size_t i;
int bi;
for (i = 0, bi = AES_BLOCKLEN; i < length; ++i, ++bi) {
if (bi == AES_BLOCKLEN) {
memcpy(buffer, ctx->Iv, AES_BLOCKLEN);
Cipher((state_t*)buffer,ctx->RoundKey);
for (bi = (AES_BLOCKLEN - 1); bi >= 0; --bi) {
if (ctx->Iv[bi] == 255) {
ctx->Iv[bi] = 0;
continue;
}
ctx->Iv[bi] += 1;
break;
}
bi = 0;
}
buf[i] = (buf[i] ^ buffer[bi]);
}
}
其他两种比较复杂,不再详细说明、也没有写相应的代码。
加密算法优化
使用32或更多比特寻址的系统,可以事先对所有可能的输入创建对应表,利用查表来实现SubBytes,ShiftRows和MixColumns步骤以达到加速的效果。这么做需要产生4个表,每个表都有256个格子,一个格子记载32位的输出;约占去4KB(4096字节)存储器空间,即每个表占去1KB的存储器空间。如此一来,在每个加密循环中,只需要查16次表,作12次32位的XOR运算,以及AddRoundKey步骤中4次32位XOR运算。若使用的平台存储器空间不足4KB,也可以利用循环交换的方式一次查一个256格32位的表。参考文章:Efficient Software Implementation of AES on 32-Bit Platforms | SpringerLink
使用一种面向字节的方法,即从字节的角度分析,可以将SubBytes, ShiftRows, MixColumns三个步骤合为一个操作。参考资料中也给出了相应的论文和实现。
不使用查找表时的优化
这种优化面向嵌入式设备,因为设备内存通常不足4KB。实际上这种优化目前已经有人完成、并且将所有的查找表替换为了实时计算。参考资料7中有详细的描述。
仅仅使用 Sbox 查找表的优化
这项工作在2003年由Bertoni等人完成,它们在低内存嵌入式设备中仅仅使用Sbox和InvSbox的情况下对AES算法进行了优化。详细内容见参考资料9,11。
算法的关键是使用了明文矩阵的转置。

这个操作非常简单,但是有一些非常有趣的结果。
结果是 SubBytes , ShiftRows, AddRoundKey 与之前的操作时类似的,但是MixColumns通过这个转置运算可以被极大地加速。
在旧的 MixColumns 中,操作是这样的,实际上是 $GF(2^8)$ 上的矩阵乘法:

每一列代价为4次乘法,4次XOR加法,3次移位操作。
总代价为 16次 $GF(2^8)$ 乘法,16次加法,12次移位以及一个中间变量。
新的 MixColumns 操作:
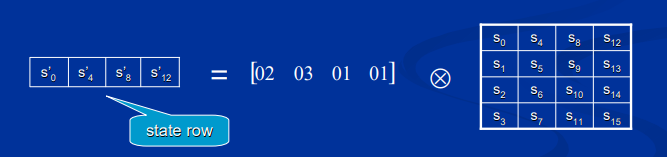
区别在于以行来处理state数组而不是按列处理。
新的 MixColumns 需要16次乘法和16次XOR运算,不需要其他操作。
解密与加密类似,详细内容查看参考资料9和11。
面向字节、全查表加密优化
理论上来讲这种方法的速度最快(如果将上面的优化结合起来应该会更快,由于时间限制,不能写出完整的代码),但是并不安全,优化的核心是将运算过程用查表的方式实现,以下是用到的几个查询表:
Sbox && InvSbox
分别是Sbox和Sbox的逆
uchar Sbox[256] = { // forward s-box
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16};
uchar InvSbox[256] = { // inverse s-box
0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb,
0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb,
0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e,
0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25,
0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92,
0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84,
0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06,
0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b,
0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73,
0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e,
0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b,
0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4,
0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f,
0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef,
0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d};
Xtime2Sbox && Xtime3Sbox
Xtime2Sbox这个表是Xtime2和Sbox的组合,即Xtime2[Sbox[]],Xtime3Sbox同理,在MixColumns加密过程中用来做有限域中的乘法,在上面的算法说明中有解释。
// combined Xtimes2[Sbox[]]
uchar Xtime2Sbox[256] = {
0xc6, 0xf8, 0xee, 0xf6, 0xff, 0xd6, 0xde, 0x91, 0x60, 0x02, 0xce, 0x56, 0xe7, 0xb5, 0x4d, 0xec,
0x8f, 0x1f, 0x89, 0xfa, 0xef, 0xb2, 0x8e, 0xfb, 0x41, 0xb3, 0x5f, 0x45, 0x23, 0x53, 0xe4, 0x9b,
0x75, 0xe1, 0x3d, 0x4c, 0x6c, 0x7e, 0xf5, 0x83, 0x68, 0x51, 0xd1, 0xf9, 0xe2, 0xab, 0x62, 0x2a,
0x08, 0x95, 0x46, 0x9d, 0x30, 0x37, 0x0a, 0x2f, 0x0e, 0x24, 0x1b, 0xdf, 0xcd, 0x4e, 0x7f, 0xea,
0x12, 0x1d, 0x58, 0x34, 0x36, 0xdc, 0xb4, 0x5b, 0xa4, 0x76, 0xb7, 0x7d, 0x52, 0xdd, 0x5e, 0x13,
0xa6, 0xb9, 0x00, 0xc1, 0x40, 0xe3, 0x79, 0xb6, 0xd4, 0x8d, 0x67, 0x72, 0x94, 0x98, 0xb0, 0x85,
0xbb, 0xc5, 0x4f, 0xed, 0x86, 0x9a, 0x66, 0x11, 0x8a, 0xe9, 0x04, 0xfe, 0xa0, 0x78, 0x25, 0x4b,
0xa2, 0x5d, 0x80, 0x05, 0x3f, 0x21, 0x70, 0xf1, 0x63, 0x77, 0xaf, 0x42, 0x20, 0xe5, 0xfd, 0xbf,
0x81, 0x18, 0x26, 0xc3, 0xbe, 0x35, 0x88, 0x2e, 0x93, 0x55, 0xfc, 0x7a, 0xc8, 0xba, 0x32, 0xe6,
0xc0, 0x19, 0x9e, 0xa3, 0x44, 0x54, 0x3b, 0x0b, 0x8c, 0xc7, 0x6b, 0x28, 0xa7, 0xbc, 0x16, 0xad,
0xdb, 0x64, 0x74, 0x14, 0x92, 0x0c, 0x48, 0xb8, 0x9f, 0xbd, 0x43, 0xc4, 0x39, 0x31, 0xd3, 0xf2,
0xd5, 0x8b, 0x6e, 0xda, 0x01, 0xb1, 0x9c, 0x49, 0xd8, 0xac, 0xf3, 0xcf, 0xca, 0xf4, 0x47, 0x10,
0x6f, 0xf0, 0x4a, 0x5c, 0x38, 0x57, 0x73, 0x97, 0xcb, 0xa1, 0xe8, 0x3e, 0x96, 0x61, 0x0d, 0x0f,
0xe0, 0x7c, 0x71, 0xcc, 0x90, 0x06, 0xf7, 0x1c, 0xc2, 0x6a, 0xae, 0x69, 0x17, 0x99, 0x3a, 0x27,
0xd9, 0xeb, 0x2b, 0x22, 0xd2, 0xa9, 0x07, 0x33, 0x2d, 0x3c, 0x15, 0xc9, 0x87, 0xaa, 0x50, 0xa5,
0x03, 0x59, 0x09, 0x1a, 0x65, 0xd7, 0x84, 0xd0, 0x82, 0x29, 0x5a, 0x1e, 0x7b, 0xa8, 0x6d, 0x2c
};
Xtime2 && Xtime9 && XtimeB && XtimeD && XtimeE
在解密时使用,用于有限域乘法,是加密多项式的乘法逆元。
uchar Xtime2[256] = {
0x00, 0x02, 0x04, 0x06, 0x08, 0x0a, 0x0c, 0x0e, 0x10, 0x12, 0x14, 0x16, 0x18, 0x1a, 0x1c, 0x1e,
0x20, 0x22, 0x24, 0x26, 0x28, 0x2a, 0x2c, 0x2e, 0x30, 0x32, 0x34, 0x36, 0x38, 0x3a, 0x3c, 0x3e,
0x40, 0x42, 0x44, 0x46, 0x48, 0x4a, 0x4c, 0x4e, 0x50, 0x52, 0x54, 0x56, 0x58, 0x5a, 0x5c, 0x5e,
0x60, 0x62, 0x64, 0x66, 0x68, 0x6a, 0x6c, 0x6e, 0x70, 0x72, 0x74, 0x76, 0x78, 0x7a, 0x7c, 0x7e,
0x80, 0x82, 0x84, 0x86, 0x88, 0x8a, 0x8c, 0x8e, 0x90, 0x92, 0x94, 0x96, 0x98, 0x9a, 0x9c, 0x9e,
0xa0, 0xa2, 0xa4, 0xa6, 0xa8, 0xaa, 0xac, 0xae, 0xb0, 0xb2, 0xb4, 0xb6, 0xb8, 0xba, 0xbc, 0xbe,
0xc0, 0xc2, 0xc4, 0xc6, 0xc8, 0xca, 0xcc, 0xce, 0xd0, 0xd2, 0xd4, 0xd6, 0xd8, 0xda, 0xdc, 0xde,
0xe0, 0xe2, 0xe4, 0xe6, 0xe8, 0xea, 0xec, 0xee, 0xf0, 0xf2, 0xf4, 0xf6, 0xf8, 0xfa, 0xfc, 0xfe,
0x1b, 0x19, 0x1f, 0x1d, 0x13, 0x11, 0x17, 0x15, 0x0b, 0x09, 0x0f, 0x0d, 0x03, 0x01, 0x07, 0x05,
0x3b, 0x39, 0x3f, 0x3d, 0x33, 0x31, 0x37, 0x35, 0x2b, 0x29, 0x2f, 0x2d, 0x23, 0x21, 0x27, 0x25,
0x5b, 0x59, 0x5f, 0x5d, 0x53, 0x51, 0x57, 0x55, 0x4b, 0x49, 0x4f, 0x4d, 0x43, 0x41, 0x47, 0x45,
0x7b, 0x79, 0x7f, 0x7d, 0x73, 0x71, 0x77, 0x75, 0x6b, 0x69, 0x6f, 0x6d, 0x63, 0x61, 0x67, 0x65,
0x9b, 0x99, 0x9f, 0x9d, 0x93, 0x91, 0x97, 0x95, 0x8b, 0x89, 0x8f, 0x8d, 0x83, 0x81, 0x87, 0x85,
0xbb, 0xb9, 0xbf, 0xbd, 0xb3, 0xb1, 0xb7, 0xb5, 0xab, 0xa9, 0xaf, 0xad, 0xa3, 0xa1, 0xa7, 0xa5,
0xdb, 0xd9, 0xdf, 0xdd, 0xd3, 0xd1, 0xd7, 0xd5, 0xcb, 0xc9, 0xcf, 0xcd, 0xc3, 0xc1, 0xc7, 0xc5,
0xfb, 0xf9, 0xff, 0xfd, 0xf3, 0xf1, 0xf7, 0xf5, 0xeb, 0xe9, 0xef, 0xed, 0xe3, 0xe1, 0xe7, 0xe5};
uchar Xtime9[256] = {
0x00, 0x09, 0x12, 0x1b, 0x24, 0x2d, 0x36, 0x3f, 0x48, 0x41, 0x5a, 0x53, 0x6c, 0x65, 0x7e, 0x77,
0x90, 0x99, 0x82, 0x8b, 0xb4, 0xbd, 0xa6, 0xaf, 0xd8, 0xd1, 0xca, 0xc3, 0xfc, 0xf5, 0xee, 0xe7,
0x3b, 0x32, 0x29, 0x20, 0x1f, 0x16, 0x0d, 0x04, 0x73, 0x7a, 0x61, 0x68, 0x57, 0x5e, 0x45, 0x4c,
0xab, 0xa2, 0xb9, 0xb0, 0x8f, 0x86, 0x9d, 0x94, 0xe3, 0xea, 0xf1, 0xf8, 0xc7, 0xce, 0xd5, 0xdc,
0x76, 0x7f, 0x64, 0x6d, 0x52, 0x5b, 0x40, 0x49, 0x3e, 0x37, 0x2c, 0x25, 0x1a, 0x13, 0x08, 0x01,
0xe6, 0xef, 0xf4, 0xfd, 0xc2, 0xcb, 0xd0, 0xd9, 0xae, 0xa7, 0xbc, 0xb5, 0x8a, 0x83, 0x98, 0x91,
0x4d, 0x44, 0x5f, 0x56, 0x69, 0x60, 0x7b, 0x72, 0x05, 0x0c, 0x17, 0x1e, 0x21, 0x28, 0x33, 0x3a,
0xdd, 0xd4, 0xcf, 0xc6, 0xf9, 0xf0, 0xeb, 0xe2, 0x95, 0x9c, 0x87, 0x8e, 0xb1, 0xb8, 0xa3, 0xaa,
0xec, 0xe5, 0xfe, 0xf7, 0xc8, 0xc1, 0xda, 0xd3, 0xa4, 0xad, 0xb6, 0xbf, 0x80, 0x89, 0x92, 0x9b,
0x7c, 0x75, 0x6e, 0x67, 0x58, 0x51, 0x4a, 0x43, 0x34, 0x3d, 0x26, 0x2f, 0x10, 0x19, 0x02, 0x0b,
0xd7, 0xde, 0xc5, 0xcc, 0xf3, 0xfa, 0xe1, 0xe8, 0x9f, 0x96, 0x8d, 0x84, 0xbb, 0xb2, 0xa9, 0xa0,
0x47, 0x4e, 0x55, 0x5c, 0x63, 0x6a, 0x71, 0x78, 0x0f, 0x06, 0x1d, 0x14, 0x2b, 0x22, 0x39, 0x30,
0x9a, 0x93, 0x88, 0x81, 0xbe, 0xb7, 0xac, 0xa5, 0xd2, 0xdb, 0xc0, 0xc9, 0xf6, 0xff, 0xe4, 0xed,
0x0a, 0x03, 0x18, 0x11, 0x2e, 0x27, 0x3c, 0x35, 0x42, 0x4b, 0x50, 0x59, 0x66, 0x6f, 0x74, 0x7d,
0xa1, 0xa8, 0xb3, 0xba, 0x85, 0x8c, 0x97, 0x9e, 0xe9, 0xe0, 0xfb, 0xf2, 0xcd, 0xc4, 0xdf, 0xd6,
0x31, 0x38, 0x23, 0x2a, 0x15, 0x1c, 0x07, 0x0e, 0x79, 0x70, 0x6b, 0x62, 0x5d, 0x54, 0x4f, 0x46};
uchar XtimeB[256] = {
0x00, 0x0b, 0x16, 0x1d, 0x2c, 0x27, 0x3a, 0x31, 0x58, 0x53, 0x4e, 0x45, 0x74, 0x7f, 0x62, 0x69,
0xb0, 0xbb, 0xa6, 0xad, 0x9c, 0x97, 0x8a, 0x81, 0xe8, 0xe3, 0xfe, 0xf5, 0xc4, 0xcf, 0xd2, 0xd9,
0x7b, 0x70, 0x6d, 0x66, 0x57, 0x5c, 0x41, 0x4a, 0x23, 0x28, 0x35, 0x3e, 0x0f, 0x04, 0x19, 0x12,
0xcb, 0xc0, 0xdd, 0xd6, 0xe7, 0xec, 0xf1, 0xfa, 0x93, 0x98, 0x85, 0x8e, 0xbf, 0xb4, 0xa9, 0xa2,
0xf6, 0xfd, 0xe0, 0xeb, 0xda, 0xd1, 0xcc, 0xc7, 0xae, 0xa5, 0xb8, 0xb3, 0x82, 0x89, 0x94, 0x9f,
0x46, 0x4d, 0x50, 0x5b, 0x6a, 0x61, 0x7c, 0x77, 0x1e, 0x15, 0x08, 0x03, 0x32, 0x39, 0x24, 0x2f,
0x8d, 0x86, 0x9b, 0x90, 0xa1, 0xaa, 0xb7, 0xbc, 0xd5, 0xde, 0xc3, 0xc8, 0xf9, 0xf2, 0xef, 0xe4,
0x3d, 0x36, 0x2b, 0x20, 0x11, 0x1a, 0x07, 0x0c, 0x65, 0x6e, 0x73, 0x78, 0x49, 0x42, 0x5f, 0x54,
0xf7, 0xfc, 0xe1, 0xea, 0xdb, 0xd0, 0xcd, 0xc6, 0xaf, 0xa4, 0xb9, 0xb2, 0x83, 0x88, 0x95, 0x9e,
0x47, 0x4c, 0x51, 0x5a, 0x6b, 0x60, 0x7d, 0x76, 0x1f, 0x14, 0x09, 0x02, 0x33, 0x38, 0x25, 0x2e,
0x8c, 0x87, 0x9a, 0x91, 0xa0, 0xab, 0xb6, 0xbd, 0xd4, 0xdf, 0xc2, 0xc9, 0xf8, 0xf3, 0xee, 0xe5,
0x3c, 0x37, 0x2a, 0x21, 0x10, 0x1b, 0x06, 0x0d, 0x64, 0x6f, 0x72, 0x79, 0x48, 0x43, 0x5e, 0x55,
0x01, 0x0a, 0x17, 0x1c, 0x2d, 0x26, 0x3b, 0x30, 0x59, 0x52, 0x4f, 0x44, 0x75, 0x7e, 0x63, 0x68,
0xb1, 0xba, 0xa7, 0xac, 0x9d, 0x96, 0x8b, 0x80, 0xe9, 0xe2, 0xff, 0xf4, 0xc5, 0xce, 0xd3, 0xd8,
0x7a, 0x71, 0x6c, 0x67, 0x56, 0x5d, 0x40, 0x4b, 0x22, 0x29, 0x34, 0x3f, 0x0e, 0x05, 0x18, 0x13,
0xca, 0xc1, 0xdc, 0xd7, 0xe6, 0xed, 0xf0, 0xfb, 0x92, 0x99, 0x84, 0x8f, 0xbe, 0xb5, 0xa8, 0xa3};
uchar XtimeD[256] = {
0x00, 0x0d, 0x1a, 0x17, 0x34, 0x39, 0x2e, 0x23, 0x68, 0x65, 0x72, 0x7f, 0x5c, 0x51, 0x46, 0x4b,
0xd0, 0xdd, 0xca, 0xc7, 0xe4, 0xe9, 0xfe, 0xf3, 0xb8, 0xb5, 0xa2, 0xaf, 0x8c, 0x81, 0x96, 0x9b,
0xbb, 0xb6, 0xa1, 0xac, 0x8f, 0x82, 0x95, 0x98, 0xd3, 0xde, 0xc9, 0xc4, 0xe7, 0xea, 0xfd, 0xf0,
0x6b, 0x66, 0x71, 0x7c, 0x5f, 0x52, 0x45, 0x48, 0x03, 0x0e, 0x19, 0x14, 0x37, 0x3a, 0x2d, 0x20,
0x6d, 0x60, 0x77, 0x7a, 0x59, 0x54, 0x43, 0x4e, 0x05, 0x08, 0x1f, 0x12, 0x31, 0x3c, 0x2b, 0x26,
0xbd, 0xb0, 0xa7, 0xaa, 0x89, 0x84, 0x93, 0x9e, 0xd5, 0xd8, 0xcf, 0xc2, 0xe1, 0xec, 0xfb, 0xf6,
0xd6, 0xdb, 0xcc, 0xc1, 0xe2, 0xef, 0xf8, 0xf5, 0xbe, 0xb3, 0xa4, 0xa9, 0x8a, 0x87, 0x90, 0x9d,
0x06, 0x0b, 0x1c, 0x11, 0x32, 0x3f, 0x28, 0x25, 0x6e, 0x63, 0x74, 0x79, 0x5a, 0x57, 0x40, 0x4d,
0xda, 0xd7, 0xc0, 0xcd, 0xee, 0xe3, 0xf4, 0xf9, 0xb2, 0xbf, 0xa8, 0xa5, 0x86, 0x8b, 0x9c, 0x91,
0x0a, 0x07, 0x10, 0x1d, 0x3e, 0x33, 0x24, 0x29, 0x62, 0x6f, 0x78, 0x75, 0x56, 0x5b, 0x4c, 0x41,
0x61, 0x6c, 0x7b, 0x76, 0x55, 0x58, 0x4f, 0x42, 0x09, 0x04, 0x13, 0x1e, 0x3d, 0x30, 0x27, 0x2a,
0xb1, 0xbc, 0xab, 0xa6, 0x85, 0x88, 0x9f, 0x92, 0xd9, 0xd4, 0xc3, 0xce, 0xed, 0xe0, 0xf7, 0xfa,
0xb7, 0xba, 0xad, 0xa0, 0x83, 0x8e, 0x99, 0x94, 0xdf, 0xd2, 0xc5, 0xc8, 0xeb, 0xe6, 0xf1, 0xfc,
0x67, 0x6a, 0x7d, 0x70, 0x53, 0x5e, 0x49, 0x44, 0x0f, 0x02, 0x15, 0x18, 0x3b, 0x36, 0x21, 0x2c,
0x0c, 0x01, 0x16, 0x1b, 0x38, 0x35, 0x22, 0x2f, 0x64, 0x69, 0x7e, 0x73, 0x50, 0x5d, 0x4a, 0x47,
0xdc, 0xd1, 0xc6, 0xcb, 0xe8, 0xe5, 0xf2, 0xff, 0xb4, 0xb9, 0xae, 0xa3, 0x80, 0x8d, 0x9a, 0x97};
uchar XtimeE[256] = {
0x00, 0x0e, 0x1c, 0x12, 0x38, 0x36, 0x24, 0x2a, 0x70, 0x7e, 0x6c, 0x62, 0x48, 0x46, 0x54, 0x5a,
0xe0, 0xee, 0xfc, 0xf2, 0xd8, 0xd6, 0xc4, 0xca, 0x90, 0x9e, 0x8c, 0x82, 0xa8, 0xa6, 0xb4, 0xba,
0xdb, 0xd5, 0xc7, 0xc9, 0xe3, 0xed, 0xff, 0xf1, 0xab, 0xa5, 0xb7, 0xb9, 0x93, 0x9d, 0x8f, 0x81,
0x3b, 0x35, 0x27, 0x29, 0x03, 0x0d, 0x1f, 0x11, 0x4b, 0x45, 0x57, 0x59, 0x73, 0x7d, 0x6f, 0x61,
0xad, 0xa3, 0xb1, 0xbf, 0x95, 0x9b, 0x89, 0x87, 0xdd, 0xd3, 0xc1, 0xcf, 0xe5, 0xeb, 0xf9, 0xf7,
0x4d, 0x43, 0x51, 0x5f, 0x75, 0x7b, 0x69, 0x67, 0x3d, 0x33, 0x21, 0x2f, 0x05, 0x0b, 0x19, 0x17,
0x76, 0x78, 0x6a, 0x64, 0x4e, 0x40, 0x52, 0x5c, 0x06, 0x08, 0x1a, 0x14, 0x3e, 0x30, 0x22, 0x2c,
0x96, 0x98, 0x8a, 0x84, 0xae, 0xa0, 0xb2, 0xbc, 0xe6, 0xe8, 0xfa, 0xf4, 0xde, 0xd0, 0xc2, 0xcc,
0x41, 0x4f, 0x5d, 0x53, 0x79, 0x77, 0x65, 0x6b, 0x31, 0x3f, 0x2d, 0x23, 0x09, 0x07, 0x15, 0x1b,
0xa1, 0xaf, 0xbd, 0xb3, 0x99, 0x97, 0x85, 0x8b, 0xd1, 0xdf, 0xcd, 0xc3, 0xe9, 0xe7, 0xf5, 0xfb,
0x9a, 0x94, 0x86, 0x88, 0xa2, 0xac, 0xbe, 0xb0, 0xea, 0xe4, 0xf6, 0xf8, 0xd2, 0xdc, 0xce, 0xc0,
0x7a, 0x74, 0x66, 0x68, 0x42, 0x4c, 0x5e, 0x50, 0x0a, 0x04, 0x16, 0x18, 0x32, 0x3c, 0x2e, 0x20,
0xec, 0xe2, 0xf0, 0xfe, 0xd4, 0xda, 0xc8, 0xc6, 0x9c, 0x92, 0x80, 0x8e, 0xa4, 0xaa, 0xb8, 0xb6,
0x0c, 0x02, 0x10, 0x1e, 0x34, 0x3a, 0x28, 0x26, 0x7c, 0x72, 0x60, 0x6e, 0x44, 0x4a, 0x58, 0x56,
0x37, 0x39, 0x2b, 0x25, 0x0f, 0x01, 0x13, 0x1d, 0x47, 0x49, 0x5b, 0x55, 0x7f, 0x71, 0x63, 0x6d,
0xd7, 0xd9, 0xcb, 0xc5, 0xef, 0xe1, 0xf3, 0xfd, 0xa7, 0xa9, 0xbb, 0xb5, 0x9f, 0x91, 0x83, 0x8d};
优化加密函数
在这个角度上,加密函数可以写为:
// encrypt one 128 bit block
void Encrypt (uchar *in, uchar *expkey, uchar *out)
{
uchar state[Nb * 4];
unsigned round;
memcpy (state, in, Nb * 4);
AddRoundKey ((unsigned *)state, (unsigned *)expkey);
for( round = 1; round < Nr + 1; round++ ) {
if( round < Nr )
MixSubColumns (state);
else
ShiftRows (state);
AddRoundKey ((unsigned *)state, (unsigned *)expkey + round * Nb);
}
memcpy (out, state, sizeof(state));
}
ShiftRows 操作的查表实现:
void ShiftRows (uchar *state)
{
uchar tmp;
// just substitute row 0
state[0] = Sbox[state[0]], state[4] = Sbox[state[4]];
state[8] = Sbox[state[8]], state[12] = Sbox[state[12]];
// rotate row 1
tmp = Sbox[state[1]], state[1] = Sbox[state[5]];
state[5] = Sbox[state[9]], state[9] = Sbox[state[13]], state[13] = tmp;
// rotate row 2
tmp = Sbox[state[2]], state[2] = Sbox[state[10]], state[10] = tmp;
tmp = Sbox[state[6]], state[6] = Sbox[state[14]], state[14] = tmp;
// rotate row 3
tmp = Sbox[state[15]], state[15] = Sbox[state[11]];
state[11] = Sbox[state[7]], state[7] = Sbox[state[3]], state[3] = tmp;
}
MixSubColumns 的查表实现:
// recombine and mix each row in a column
void MixSubColumns (uchar *state)
{
uchar tmp[4 * Nb];
// mixing column 0
tmp[0] = Xtime2Sbox[state[0]] ^ Xtime3Sbox[state[5]] ^ Sbox[state[10]] ^ Sbox[state[15]];
tmp[1] = Sbox[state[0]] ^ Xtime2Sbox[state[5]] ^ Xtime3Sbox[state[10]] ^ Sbox[state[15]];
tmp[2] = Sbox[state[0]] ^ Sbox[state[5]] ^ Xtime2Sbox[state[10]] ^ Xtime3Sbox[state[15]];
tmp[3] = Xtime3Sbox[state[0]] ^ Sbox[state[5]] ^ Sbox[state[10]] ^ Xtime2Sbox[state[15]];
// mixing column 1
tmp[4] = Xtime2Sbox[state[4]] ^ Xtime3Sbox[state[9]] ^ Sbox[state[14]] ^ Sbox[state[3]];
tmp[5] = Sbox[state[4]] ^ Xtime2Sbox[state[9]] ^ Xtime3Sbox[state[14]] ^ Sbox[state[3]];
tmp[6] = Sbox[state[4]] ^ Sbox[state[9]] ^ Xtime2Sbox[state[14]] ^ Xtime3Sbox[state[3]];
tmp[7] = Xtime3Sbox[state[4]] ^ Sbox[state[9]] ^ Sbox[state[14]] ^ Xtime2Sbox[state[3]];
// mixing column 2
tmp[8] = Xtime2Sbox[state[8]] ^ Xtime3Sbox[state[13]] ^ Sbox[state[2]] ^ Sbox[state[7]];
tmp[9] = Sbox[state[8]] ^ Xtime2Sbox[state[13]] ^ Xtime3Sbox[state[2]] ^ Sbox[state[7]];
tmp[10] = Sbox[state[8]] ^ Sbox[state[13]] ^ Xtime2Sbox[state[2]] ^ Xtime3Sbox[state[7]];
tmp[11] = Xtime3Sbox[state[8]] ^ Sbox[state[13]] ^ Sbox[state[2]] ^ Xtime2Sbox[state[7]];
// mixing column 3
tmp[12] = Xtime2Sbox[state[12]] ^ Xtime3Sbox[state[1]] ^ Sbox[state[6]] ^ Sbox[state[11]];
tmp[13] = Sbox[state[12]] ^ Xtime2Sbox[state[1]] ^ Xtime3Sbox[state[6]] ^ Sbox[state[11]];
tmp[14] = Sbox[state[12]] ^ Sbox[state[1]] ^ Xtime2Sbox[state[6]] ^ Xtime3Sbox[state[11]];
tmp[15] = Xtime3Sbox[state[12]] ^ Sbox[state[1]] ^ Sbox[state[6]] ^ Xtime2Sbox[state[11]];
memcpy (state, tmp, sizeof(tmp));
}
这个函数将SubBytes,ShiftRows,MixColumns 三个函数结合在一起,其中XtimeXSbox[]等于XtimeX[Sbox[]]。
AddRoundKey 操作与前面的算法是一致的:
void AddRoundKey (unsigned *state, unsigned *key)
{
int idx;
for( idx = 0; idx < 4; idx++ )
state[idx] ^= key[idx];
}
解密函数优化
与加密类似,解密也采用查表实现。
void Decrypt (uchar *in, uchar *expkey, uchar *out)
{
uchar state[Nb * 4];
unsigned round;
memcpy (state, in, sizeof(state));
AddRoundKey ((unsigned *)state, (unsigned *)expkey + Nr * Nb);
InvShiftRows(state);
for( round = Nr; round--; )
{
AddRoundKey ((unsigned *)state, (unsigned *)expkey + round * Nb);
if( round )
InvMixSubColumns (state);
}
memcpy (out, state, sizeof(state));
}
InvShiftRows 实现:
void InvShiftRows (uchar *state)
{
uchar tmp;
// restore row 0
state[0] = InvSbox[state[0]], state[4] = InvSbox[state[4]];
state[8] = InvSbox[state[8]], state[12] = InvSbox[state[12]];
// restore row 1
tmp = InvSbox[state[13]], state[13] = InvSbox[state[9]];
state[9] = InvSbox[state[5]], state[5] = InvSbox[state[1]], state[1] = tmp;
// restore row 2
tmp = InvSbox[state[2]], state[2] = InvSbox[state[10]], state[10] = tmp;
tmp = InvSbox[state[6]], state[6] = InvSbox[state[14]], state[14] = tmp;
// restore row 3
tmp = InvSbox[state[3]], state[3] = InvSbox[state[7]];
state[7] = InvSbox[state[11]], state[11] = InvSbox[state[15]], state[15] = tmp;
}
InvMixSubColumns 实现:
void InvMixSubColumns (uchar *state)
{
uchar tmp[4 * Nb];
int i;
// restore column 0
tmp[0] = XtimeE[state[0]] ^ XtimeB[state[1]] ^ XtimeD[state[2]] ^ Xtime9[state[3]];
tmp[5] = Xtime9[state[0]] ^ XtimeE[state[1]] ^ XtimeB[state[2]] ^ XtimeD[state[3]];
tmp[10] = XtimeD[state[0]] ^ Xtime9[state[1]] ^ XtimeE[state[2]] ^ XtimeB[state[3]];
tmp[15] = XtimeB[state[0]] ^ XtimeD[state[1]] ^ Xtime9[state[2]] ^ XtimeE[state[3]];
// restore column 1
tmp[4] = XtimeE[state[4]] ^ XtimeB[state[5]] ^ XtimeD[state[6]] ^ Xtime9[state[7]];
tmp[9] = Xtime9[state[4]] ^ XtimeE[state[5]] ^ XtimeB[state[6]] ^ XtimeD[state[7]];
tmp[14] = XtimeD[state[4]] ^ Xtime9[state[5]] ^ XtimeE[state[6]] ^ XtimeB[state[7]];
tmp[3] = XtimeB[state[4]] ^ XtimeD[state[5]] ^ Xtime9[state[6]] ^ XtimeE[state[7]];
// restore column 2
tmp[8] = XtimeE[state[8]] ^ XtimeB[state[9]] ^ XtimeD[state[10]] ^ Xtime9[state[11]];
tmp[13] = Xtime9[state[8]] ^ XtimeE[state[9]] ^ XtimeB[state[10]] ^ XtimeD[state[11]];
tmp[2] = XtimeD[state[8]] ^ Xtime9[state[9]] ^ XtimeE[state[10]] ^ XtimeB[state[11]];
tmp[7] = XtimeB[state[8]] ^ XtimeD[state[9]] ^ Xtime9[state[10]] ^ XtimeE[state[11]];
// restore column 3
tmp[12] = XtimeE[state[12]] ^ XtimeB[state[13]] ^ XtimeD[state[14]] ^ Xtime9[state[15]];
tmp[1] = Xtime9[state[12]] ^ XtimeE[state[13]] ^ XtimeB[state[14]] ^ XtimeD[state[15]];
tmp[6] = XtimeD[state[12]] ^ Xtime9[state[13]] ^ XtimeE[state[14]] ^ XtimeB[state[15]];
tmp[11] = XtimeB[state[12]] ^ XtimeD[state[13]] ^ Xtime9[state[14]] ^ XtimeE[state[15]];
for( i=0; i < 4 * Nb; i++ )
state[i] = InvSbox[tmp[i]];
}
查表存在的问题
然而,实际实现中应避免使用这样的对应表,否则可能因为产生缓存命中与否的差别而使侧信道攻击成为可能。
利用AES-NI指令进行优化
这一部分详细资料在参考资料12,即Intel AES-NI白皮书。
利用硬件指令的优化是软件实现的降维打击,可以做到 $1.3 cycles/sec$,甚至可以做到 $0.36cycles/sec$。
在Crypo++官方benchmark例程中,CTR模式AES速度轻松达到 $4400Mb/sec$ 。在参考资料14中给出了crypo++的源代码,试着阅读之后,由于时间关系还是放弃了分析。
下面是基本没有优化的使用AES-NI实现的AES算法,首先是加密函数:
#define DO_ENC_BLOCK(m,k) \
do{\
m = _mm_xor_si128 (m, k[ 0]); \
m = _mm_aesenc_si128 (m, k[ 1]); \
m = _mm_aesenc_si128 (m, k[ 2]); \
m = _mm_aesenc_si128 (m, k[ 3]); \
m = _mm_aesenc_si128 (m, k[ 4]); \
m = _mm_aesenc_si128 (m, k[ 5]); \
m = _mm_aesenc_si128 (m, k[ 6]); \
m = _mm_aesenc_si128 (m, k[ 7]); \
m = _mm_aesenc_si128 (m, k[ 8]); \
m = _mm_aesenc_si128 (m, k[ 9]); \
m = _mm_aesenclast_si128(m, k[10]);\
}while(0)
static void aes128_enc(__m128i *key_schedule, uint8_t *plainText,uint8_t *cipherText){
__m128i m = _mm_loadu_si128((__m128i *) plainText);
DO_ENC_BLOCK(m,key_schedule);
_mm_storeu_si128((__m128i *) cipherText, m);
}
解密函数:
#define DO_DEC_BLOCK(m,k) \
do{\
m = _mm_xor_si128 (m, k[10+0]); \
m = _mm_aesdec_si128 (m, k[10+1]); \
m = _mm_aesdec_si128 (m, k[10+2]); \
m = _mm_aesdec_si128 (m, k[10+3]); \
m = _mm_aesdec_si128 (m, k[10+4]); \
m = _mm_aesdec_si128 (m, k[10+5]); \
m = _mm_aesdec_si128 (m, k[10+6]); \
m = _mm_aesdec_si128 (m, k[10+7]); \
m = _mm_aesdec_si128 (m, k[10+8]); \
m = _mm_aesdec_si128 (m, k[10+9]); \
m = _mm_aesdeclast_si128(m, k[0]);\
}while(0)
static void aes128_dec(__m128i *key_schedule, uint8_t *cipherText,uint8_t *plainText){
__m128i m = _mm_loadu_si128((__m128i *) cipherText);
DO_DEC_BLOCK(m,key_schedule);
_mm_storeu_si128((__m128i *) plainText, m);
}
优化结果
仅仅使用 Sbox 查找表的优化
以CPU周期数为计量单位,仅仅使用Sbox加解密时,测试的结果如下:
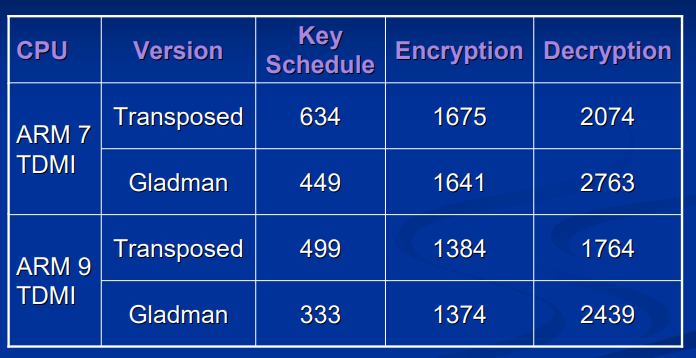
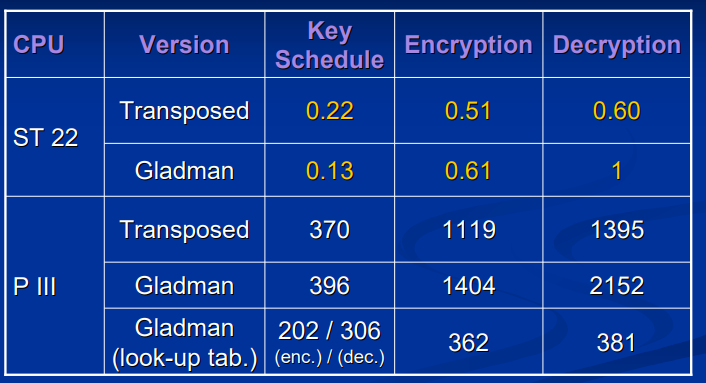
与 Gladman 给出的算法的对比:
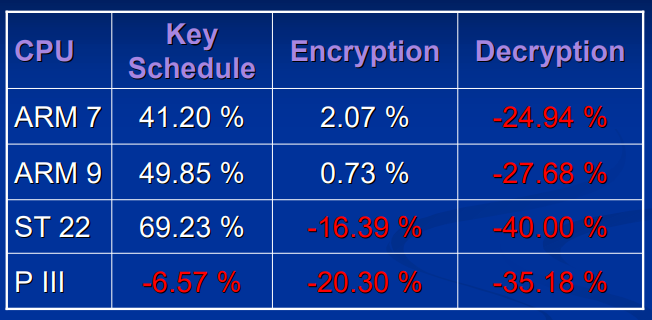
可以看到算法在解密方面提升很大。
面向字节、全查表优化结果

经过五次运行测试,取平均值最终得到的结果如下:
| 加密时间(CPU cycle) | 解密时间(CPU cycle) |
|---|---|
| 73 | 111 |
测试的CPU为 Intel(R) Core(TM) i5-9300H CPU @ 2.40GHz,主频2400MHz。
加密速率 $ES = cpu_{fre}/t_{encrypt} = 2400 * 10^6/73 =32.88 * 10^6bytes/sec$
解密速率 $DS=cpu_{fre}/t_{decrypt}=2400*106/111=21.62*106bytes/sec$
使用AES-NI指令优化结果

6.04452s内完成了789949975次AES操作。
加密速率 $ES = 789949975/6.04452*16bytes/sec=1994.15Mb/s$
通过读取随机文件得到的结果:
用 dd 命令生成随机文件。

这里读取随机文件大小为16MB,速率为 inf,但是使用 clock() 函数测量会导致结果不准确,然而使用 rdstc 汇编指令出现了一些问题。可能由于解密速率过大,导致 clock()函数两次返回值相同。
所以将设置文件大小为168MB,再次运行:

加密速率为 $3902.44Mb/s$
解密速率为 $2711.86Mb/s$
多次运行,加密速率最高达到 $4705.88Mb/s$

多次运行,解密速率最高达到 $4102.56Mb/s$

参考资料
- AES implementations - Wikipedia
- Advanced Encryption Standard - Wikipedia
- Cryptography - 256 bit ciphers (embeddedsw.net)
- The Rijndael Page (archive.org)
- kokke/tiny-AES-c: Small portable AES128/192/256 in C (github.com)
- AES五种加密模式(CBC、ECB、CTR、OCF、CFB) - 月之星狼 - 博客园 (cnblogs.com)
- A byte-oriented AES-256 implementation - Literatecode
- High-Speed Area-Efficient Implementation of AES Algorithm on Reconfigurable Platform | IntechOpen
- Efficient Software Implementation of AES on 32-Bit Platforms | SpringerLink
- Google Code Archive - Long-term storage for Google Code Project Hosting.
- Microsoft PowerPoint - Bertoni (iacr.org)
- Efficient AES Implementations on Westmere (intel.com)
- AES-NI Performance Analyzed; Limited To 32nm Core i5 CPUs | Tom's Hardware (tomshardware.com)
- Release Crypto++ 8.6 release · weidai11/cryptopp (github.com)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号