WeetCode3 暴力递归->记忆化搜索->动态规划
笔者这里总结的是一种套路,这种套路笔者最先是从左程云的b站视频学习到的
本文进行简单总结
一丶动态规划的思想
使用dp数组记录之前状态计算的最佳结果,找出当前状态和之前状态的关系(状态转移方程)然后使用状态转移方程,计算处当前状态最佳结果,然后更新dp数组,填完dp数组即得到最佳结果
本质是空间换时间
二丶动态规划的难点
状态转移方程,这个概念比较难理解,更难想出具体题目的状态转移方程
本文就是为了解决这种痛点
我们从暴力递归写起,然后优化成记忆化搜索,然后根据递归大任务和小任务的关系,得到状态转移方程,优化成动态规划。
三丶暴力递归->记忆化搜索->动态规划
1.从一道题说起
现在存在一个机器人,整数N表示存在N个位置,机器人可以位于1~N上的任意一个位置,
S位机器人初始位置(当然N>=S>=1)E表示机器人的目标位置,K表示机器人可以走多少步,机器人必须走完K步,只能向左or向右且不可以停留在一个位置不走,请问机器人从S到E右多少中走法
例如N=5 机器人可以位于【1,2,3,4,5】S=2,机器人起始位于2,E=4 机器人目标位置位4,机器人必须走完K=4
存在可行方案:
2->3->4->5->4
2->3->4->3->4
2->3->2->3->4
2->1->2->3->4
- 第一反应:纯纯动态规划,开始找状态转移方程,如何找到状态转移方程不是本文的重点我们从暴力递归讲起
2.暴力递归解题
暴力递归的关键是如何【尝试】,尝试依赖于刷题的经验
-
分析:
- 如果机器人当前还有剩余步数要走
- 机器人位于1位置,它只能向右,因为只能位于1~N位置上
- 如果机器人位于N位置,它只能向左,因为只能位于1~N位置上
- 如果机器人位于2~N-1位置,它可以向左or向右
当然每走一步剩余步数需要减1- 如果机器人当前没有剩余部署要走
- 如果机器人走到了目标位置,我们返回1,因为这是一种可行的机器人移动方案
- 如果机器人当前不在目标位置,因为没有步数走,还不在目标位置,说明这样走不可行
- 如果机器人当前还有剩余步数要走
-
根据分析写出暴力递归方法
- 我们可以知道递归出口baseCase位当前剩余步数等于0,无论是否在目标位置,我们都将返回0,1,因为无路可走
- 当机器人位于1 or N的时候只可以向右or向左
- 机器人位于中间位置,存在两个方向,可以向左和向右
/** * @param N 1~N可以停留 * @param S 机器人起始位置 * @param E 机器人目标位置 * @param K 总步数 * @return int 总共的走法 */ public static int moveWayCount(int N, int S, int E, int K) { return Recursion.recursion(N, S, E, K); } /**** * 递归怎么做 */ static class Recursion { /** * @param N 1~N可以停留 * @param curIndex 机器人当前位置 * @param E 机器人目标位置 * @param resetStep 剩余步数 * @return int 总共的走法 */ static int recursion(int N, int curIndex, int E, int resetStep) { //递归出口baseCase位当前剩余步数等于0,无论是否在目标位置,我们都将返回0,1,因为无路可走 if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //当机器人位于1orN的时候只可以向右or向左 if (curIndex == 1) { return recursion(N, 2, E, resetStep - 1); } if (curIndex == N) { return recursion(N, N - 1, E, resetStep - 1); } //机器人位于中间位置,存在两个方向,可以向左和向右 return recursion(N, curIndex + 1, E, resetStep - 1) + recursion(N, curIndex - 1, E, resetStep - 1); } }其实还可以加一个剪枝条件,如果当前的步数那怕机器人向着目标地点一直前进都无法到达那么直接返回0(Math.abs(curIndex-E)<restStep 直接返回0) 但是这个不是本文的关键,遂不表于代码中 -
时间复杂度分析,如果机器人位于中间位置,递归树是一个二叉树,树的高度是K,因为需要走K步,那么时间复杂度2的k次幂
-
空间复杂度,递归树高度位K,O(K)
-
如何优化
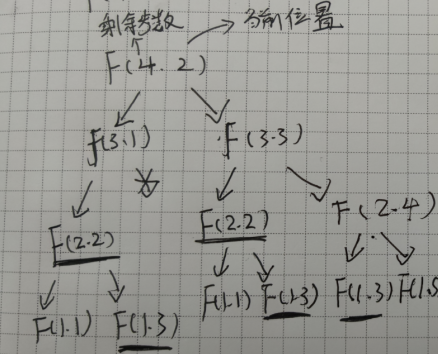
- 观察上面的递归树(没有画到叶子节点,但是足以说明问题)
- 我们进行了重复的计算 F(3,1)和F(3,3)都依赖了F(2,3)
- 我们可以使用使用缓存在减少重复计算,具体见【三丶记忆化搜索】
- 观察上面的递归树(没有画到叶子节点,但是足以说明问题)
3.记忆化搜索解题
-
记忆化搜索的思想:使用缓存减少递归的重复计算
-
观察上面的递归方法的方法签名:
int recursion(int N, int curIndex, int E, int resetStep)N和E是两个固定的参数,递归方法返回值取决于curIndex,和resetStep
- curIndex的大小范围是1~N
- resetStep的大小范围时0~K
-
所以我们只需要使用一个一个(N+1)*(K+1)的二位数组来缓存递归的答案
如果答案已经有了,那我们直接取数组的值,反之递归求答案,写答案到数组中即可(当然你也可以使用map来缓存答案,但是为了更好过渡到动态规划的解法,我们这里使用二维数组)
-
-
代码:
/** * @param N 1~N可以停留 * @param S 机器人起始位置 * @param E 机器人目标位置 * @param K 总步数 * @return int 总共的走法 */ public static int moveWayCount(int N, int S, int E, int K) { // return Recursion.recursion(N, S, E, K); int[][] memory = new int[N + 1][K + 1]; for (int row = 0; row < memory.length; row++) { Arrays.fill(memory[row], -1); } return MemorySearch.recursion(N, S, E, K, memory); } /**** * 记忆化搜索 */ static class MemorySearch { /** * @param N 1~N可以停留 * @param curIndex 机器人当前位置 * @param E 机器人目标位置 * @param resetStep 剩余步数 * @param memory 优化递归的记忆数组 * @return int 总共的走法 */ static int recursion(int N, int curIndex, int E, int resetStep, int[][] memory) { int res; if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //如果没有命中缓存 if (memory[curIndex][resetStep] == -1) { //求值 if (curIndex == 1) { res = recursion(N, 2, E, resetStep - 1, memory); } else if (curIndex == N) { res = recursion(N, N - 1, E, resetStep - 1, memory); } else { res = recursion(N, curIndex + 1, E, resetStep - 1, memory) + recursion(N, curIndex - 1, E, resetStep - 1, memory); } //写缓存 memory[curIndex][resetStep] = res; } else { //命中缓存 返回缓存内容即可 res = memory[curIndex][resetStep]; } return res; } } -
时间复杂度,我们一共求解了N*K次来填满memory数组,每一次求解的时间复杂度O(1)总时间复杂度O(NxK)
-
空间复杂度,O(NxK)
4.动态规划解题
-
写在前面,和记忆化搜索相比动态规划并没有时间复杂度,空间复杂度的提升,只是更专注于状态的转移
-
如何改成动态规划
应该敏感的知道这题可以用动态规划,定义一个 int[][] dp = new int[N + 1][K + 1];作为dp数组-
从暴力递归获取状态转移的规律
这个图方便理解,如何推出的看下方
-
如何初始化dp数组
if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //从这段代码我们可以知道dp的第一行除了E那一列全为0, //只有dp[0][E]=1 -
第一个状态转移方程
if (curIndex == 1) { return recursion(N, 2, E, resetStep - 1)s; } //可以知道当 位于第一列的时候,dp[1][剩余步数]=dp[2][剩余步数-1],也就是右上角的值 -
第二个状态转移方程
if (curIndex == N) { return recursion(N, N - 1, E, resetStep - 1); } //可以知道当 位于第N列的时候,dp[N-1][剩余步数]=dp[2][剩余步数-1] 也就左上角的值 -
第三个状态转移方程
//机器人位于中间位置,存在两个方向,可以向左和向右 return recursion(N, curIndex + 1, E, rzesetStep - 1) + recursion(N, curIndex - 1, E, resetStep - 1); //当不位于 【边界】的时候 //recursion(N, curIndex + 1, E, resetStep - 1) 右上角的值 //recursion(N, curIndex - 1, E, resetStep - 1)左上角 //如果 curIndex!=1 and curIndex!=N //dp[curIndex][剩余步数]=dp[curIndex+1][剩余步数-1]+dp[curIndex-1][剩余步数-1]
-
-
-
代码:
static class DynamicProgramming { /** * @param N 1~N可以停留 * @param S 机器人起始位置 * @param E 机器人目标位置 * @param K 总步数 * @return int 总共的走法 */ static int dynamicProgramming(int N, int S, int E, int K) { int[][] dp = new int[K + 1][N + 1]; dp[0][E] = 1; for (int restStep = 1; restStep <= K; restStep++) { for (int cur = 1; cur <= N; cur++) { if (cur == 1) { dp[restStep][cur] = dp[restStep - 1][2]; continue; } else if (cur == N) { dp[restStep][cur] = dp[restStep - 1][N - 1]; continue; } dp[restStep][cur] = dp[restStep - 1][cur + 1] + dp[restStep - 1][cur - 1]; } } return dp[K][S]; } }
至此,我们可以看出递归,记忆化搜索,动态规划,具备一定的联系
5.递归改动态规划的套路
- 难点在,如何【尝试】怎么可以相到一个合理的尝试方式并且写出递归代码
- 如何改动态规划
- 看递归方法可变参数的个数,这个可变参数的个数决定了dp数组的大小和维度
- 看调用递归的方法的入入参,可以知道我们的最终目的是dp中的哪一项
- 根据递归的baseCase初始化dp数组
- 根据递归中当前方法栈的返回值依赖于哪些递归的返回值,根据这个我们可以得到状态转移方程,
- 根据当前位置依赖于哪些位置,可以知道动态规划for循环怎么写,从上到下,还是从下到上,从左到右还是从右到左
四丶使用套路解几道题
1.换钱最少的货币数
【题目】
给定数组arr, arr中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,
再给定一个整数aim,代表要找的钱数,求组成aim的最少货币数。
【举例】
arr=[5,2,3],aim=20
4张5元可以组成20元,其他找钱方案都要使用更多的货币,所以返回4.
arr=[5,2,3],aim=0
不用任何货币就可以组成0元,返回0
arr=[3,5],aim=2
根本没法组成2元,钱不能找开的情况下默认返回-1.
-
暴力递归
/**** * 递归解法 */ static class Recursion { /*** * 最少使用多少张 amountArray 中钱才能凑出目标钱 * @param amountArray 货币数组 * @param targetMoneyToChange 目标凑成钱 * @return 最少使用几张 */ static int minAmountMoneyToChange(int[] amountArray, int targetMoneyToChange) { return recursion(amountArray, 0, targetMoneyToChange); } /*** * 对当前钱的选择做出抉择 * 可以选择不选择当前的钱,也可以选择当前的钱,取小者 * 如果选择当前钱,无法凑出目标钱数 那么返回-1 * @param amountArray 货币数组 * @param nowChooseIndex 当前选择到amountArray的那个位置的硬币 * @param restMoney 剩余的需要凑出来的钱 * @return 当前决策最少需要多少张(可以选择不选择当前的钱,也可以选择当前的钱,取小者) */ static int recursion(int[] amountArray, int nowChooseIndex, int restMoney) { //当前剩余的钱为0 if (restMoney == 0) { //返回0 表示不选择当前位置的钱,所以选择对凑出目标钱数的影响是0 return 0; } if (restMoney < 0) { //如果restMoney小于0 说明选择的钱太多了,之前做的选择是错误的 return -1; } //如果当前选择的已经到达货币数组的极限 没有办法选择更多的钱了 if (nowChooseIndex >= amountArray.length) { return -1; } //能走到这儿说明 剩余的钱不为0,也不为负数,且还有选择的机会 //如果不选择当前的钱 选择的位置+1(向后做出选择)剩余的前数不变因为我们不选择当前的钱 int noChooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney); //选择当前的钱 剩余钱减少当前选择钱的面值 int chooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]); //无论是否选择当前钱 or 不选择当前钱,都木有办法凑出目标钱 那么返回-1 //如100,200,300,凑5,选择100 or不选择100都没法凑出5返回-1 if (noChooseNow == -1 && chooseNow == -1) { return -1; } //如果不选择当前钱,我们再也无法凑出来目标面值的钱 //比如2 100 3凑5 如果放弃了2我们再也没有办法凑出5元钱了 所以我们必须持有这张2 if (noChooseNow == -1) { //那么我们必须做出选择当前钱的抉择,选择当前钱那么+1(因为选择了当前钱,张数+1) return chooseNow + 1; } //选择当前钱了我们再也无法凑出目标钱 那么我们只能做出不选择当前钱的抉择 //比如 100,2,3凑出5 选择了100我们不可能凑出5了 我们只能放弃100 if (chooseNow == -1) { return noChooseNow; } //反之我们可以选择选当前钱,可以 不选择当前钱,因为找最少的货币数 //那么取较小者 return Math.min(chooseNow + 1, noChooseNow); } } -
记忆化搜索
观察上述递归方法
static int recursion(int[] amountArray, int nowChooseIndex, int restMoney) { int[] amountArrays是一个不会变化的数组(选择的时候还改变这个钱那就是来捣乱的) nowChooseIndex 介于 0~amountArrays.length-1 restMoney介于0~目标凑出来的钱数 需要说明的是 restMoneny可以到达负数,但是负数是固定返回-1的so记忆化搜索需要的数组只需要是一个二维数组 or使用hashMap 这个题使用hashMap效果可能更好,因为 restMoney 的值取决于amountArray,比如amountArray=【5,10,20】目标钱为15,restMoney永远不可能到达1 2 3这些数目,所以使用二位数组存在浪费,当前最坏情况空间复杂度一样 如果使用数组 那么数组需要被初始化为-2,因为-1是无效解,0是有效解,所以使用-2具体代码没啥难度不写了
-
动态递归
我们需要根据递归的代码推断出状态转移方程
使用amountArray=【2,3,5,7,2】targetMoneyToChange=10为例子-
我们的目标是什么
return recursion(amountArray, 0, targetMoneyToChange); 目标是dp[0][10] -
dp数组的大小
int[][]dp=new int[amountArray.length+1][targetMoneyToChange+1] //因为存在行越界的情况,钱10的意义是restMoney=10 是具有意义的 //new int[6][11] -
如何初始化dp数组
1.第一列置为0
//当前剩余的钱为0 if (restMoney == 0) { //返回0 表示不选择当前位置的钱,所以选择对凑出目标钱数的影响是0 return 0; }2.列小于0一律返回-1
if (restMoney < 0) { //如果restMoney小于0 说明选择的钱太多了,之前做的选择是错误的 return -1; }3.行大于等于amountArray.length一律返回-1
其实我们dp数组行大小为amountArray.length+1,去到amountArray.length+1后序不为++,所以这一句其实是把最后一行置为-1,到底是代码逻辑处理这个情况,还是多弄一行,取决于dp数组如何设计
//如果当前选择的已经到达货币数组的极限 没有办法选择更多的钱了 if (nowChooseIndex >= amountArray.length) { return -1; } -
状态转移
假如当前restMoney=6 nowChooseIndx=2
int noChooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney); int chooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]);依赖于 nowChooseIndex + 1,restMoney的值也就是 dp【3】【6】的值
依赖nowChooseIndex+1,restMoney - amountArray[nowChooseIndex]的值
也就是dp【3】【6-amountArray[2]】的值,
总而言之,当前行的求解依赖于下一行,当前列的求解依赖于左边列,左边第几列需要从amountArray中取
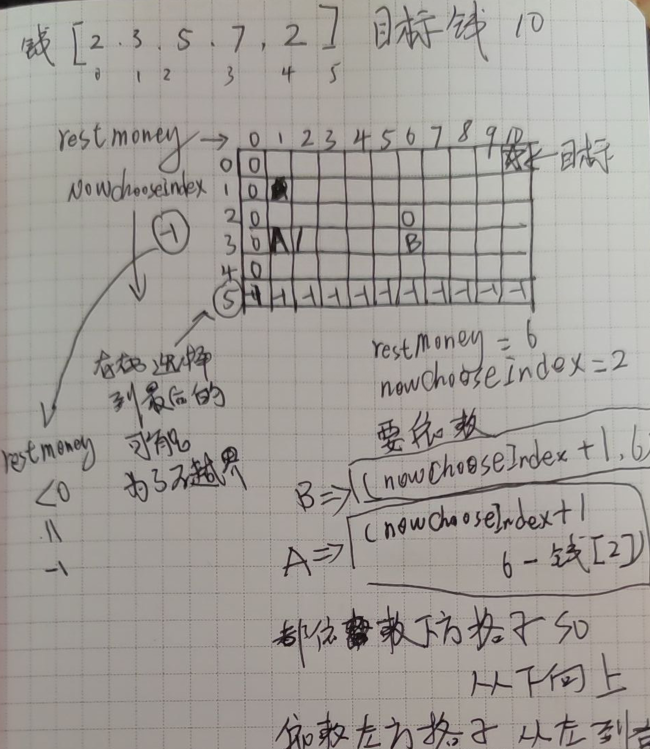
写代码发现dp【5】【0】不可以设置为-1 因为这个位置表示的是剩余钱为0,当前选到最后一个货币,这是一个可行解,他喵的害我还久debug不出来
-
代码
/*** * 最少使用多少张 amountArray 中钱才能凑出目标钱 * @param amountArray 货币数组 * @param targetMoneyToChange 目标凑成钱 * @return 最少使用几张 */ static int minAmountMoneyToChange(int[] amountArray, int targetMoneyToChange) { int len = amountArray.length; int[][] dp = new int[len + 1][targetMoneyToChange + 1]; //初始化 Arrays.fill(dp[0], 0); for (int col = 1; col < targetMoneyToChange + 1; col++) { dp[len][col] = -1; } System.out.println(ArrayUtils.toString(dp)); for (int nowChooseIndex = len - 1; nowChooseIndex >= 0; nowChooseIndex--) { for (int restMoney = 1; restMoney <= targetMoneyToChange; restMoney++) { // int noChooseNow = valueInAmountArray(dp, nowChooseIndex + 1, restMoney); // int chooseNow = valueInAmountArray(dp, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]); // dp[nowChooseIndex][restMoney] = doPolicyDecision(noChooseNow, chooseNow); int noChooseNow = dp[nowChooseIndex + 1][restMoney]; int chooseNow = -1; if (restMoney - amountArray[nowChooseIndex] >= 0) { chooseNow = dp[nowChooseIndex + 1][restMoney - amountArray[nowChooseIndex]]; } if (noChooseNow == -1 && chooseNow == -1) { dp[nowChooseIndex][restMoney] = -1; continue; } //如果不选择当前钱,我们再也无法凑出来目标面值的钱 //比如2 100 3凑5 如果放弃了2我们再也没有办法凑出5元钱了 所以我们必须持有这张2 if (noChooseNow == -1) { //那么我们必须做出选择当前钱的抉择,选择当前钱那么+1(因为选择了当前钱,张数+1) dp[nowChooseIndex][restMoney] = chooseNow + 1; continue; } //选择当前钱了我们再也无法凑出目标钱 那么我们只能做出不选择当前钱的抉择 //比如 100,2,3凑出5 选择了100我们不可能凑出5了 我们只能放弃100 if (chooseNow == -1) { dp[nowChooseIndex][restMoney] = noChooseNow; continue; } //反之我们可以选择选当前钱,可以 不选择当前钱,因为找最少的货币数 //那么取较小者 dp[nowChooseIndex][restMoney] = Math.min(chooseNow + 1, noChooseNow); } } System.out.println(ArrayUtils.toString(dp)); return dp[0][targetMoneyToChange]; }
-
2.马踏棋盘
中国象棋,可以想象成一个int[8][10]的二维数组,马棋子最开始位于(0,0)位置,去往目标位置(x,y)必须走step步,问一共存在多少种的走法
-
思路
从【0,0】使用step步到【x,y】等价于使用step-1步到【x-1,y+2】,【x+1,y+2】....(这些步骤再跳一步就可以到【x,y】了)
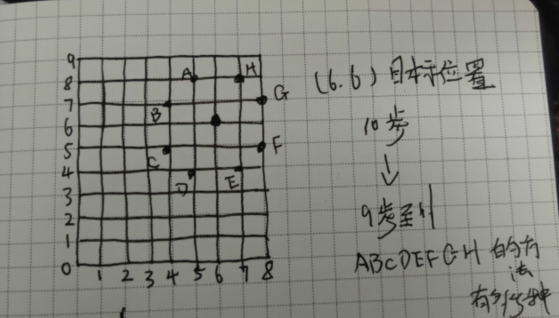
-
暴力递归
- baseCase:越界了那么当前这种跳法不行。or 步数用完了如果当前位置是目标位置那么返回1表示这是一种可行的跳法,反之返回0表示这个跳法不行
static class Recursion { static int horseJumpToTargetPosition(int x, int y, int step) { return recursion(x, y, step); } /*** * 起始位于0 0 去往目标位置 x y 必须走step步 * * 但是代码的写法是从 x,y 跳向 0 ,0用step步 * 二者等价 * @param x 目标位置的横坐标 * @param y 目标位置的纵坐标 * @param step 需要走多少步 * @return 一共多少中走法 */ static int recursion(int x, int y, int step) { //如果越界那么说明当前递归树的分支不得行 if (!checkPosition(x, y)) { return 0; } //如果步数用完了 if (step == 0) { //是在 0 0 位置 那么是一种跳法 if (x == 0 && y == 0) { return 1; } else { //反之此跳法不得行 return 0; } } return //假如当前位置(6,6)依赖于(5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7) recursion(x - 1, y + 2, step - 1) + recursion(x + 1, y + 2, step - 1) + recursion(x + 2, y + 1, step - 1) + recursion(x + 2, y - 1, step - 1) + recursion(x + 1, y - 2, step - 1) + recursion(x - 1, y - 2, step - 1) + recursion(x - 2, y - 1, step - 1) + recursion(x - 2, y + 1, step - 1) ; } /** * 检查马儿当前位置是否越界 跳出棋盘外 * * @param x 横坐标 * @param y 纵坐标 * @return 是否越界 越界返回false */ private static boolean checkPosition(int x, int y) { return x >= 0 && x <= 8 && y >= 0 && y <= 9; } -
动态规划
-
使用递归到动态规划的套路
-
看递归方法可变参数的个数,这个可变参数的个数决定了dp数组的大小和维度
可变参数三个 所以三维数组,大小是棋盘的大小,第三维大小是step+1 -
看调用递归的方法的入参,可以知道我们的最终目的是dp中的哪一项
recursion(x, y, step);所以返回dp[x][y][step] -
根据递归的baseCase初始化dp数组
//如果越界那么说明当前递归树的分支不得行 if (!checkPosition(x, y)) { return 0; } //意味着如果我们取dp数组中的值越界了返回0//如果步数用完了 if (step == 0) { //是在 0 0 位置 那么是一种跳法 if (x == 0 && y == 0) { return 1; } else { //反之此跳法不得行 return 0; } } //意味着 dp[0][0][0]初始化为1 其余的点为0【因为我们起点定为了0】 -
根据递归中当前方法栈的返回值依赖于哪些递归的返回值,根据这个我们可以得到状态转移方程,
recursion(x - 1, y + 2, step - 1) + recursion(x + 1, y + 2, step - 1) + recursion(x + 2, y + 1, step - 1) + recursion(x + 2, y - 1, step - 1) + recursion(x + 1, y - 2, step - 1) + recursion(x - 1, y - 2, step - 1) + recursion(x - 2, y - 1, step - 1) + recursion(x - 2, y + 1, step - 1) //step看作z轴,当前层的值只依赖于下面层值 //dp[x][y][step]= // dp[x - 1][ y + 2]+[step - 1] //+ dp[x + 1][ y + 2]+[step - 1] //.....需要注意越界返回0这点 -
根据当前位置依赖于哪些位置,可以知道动态规划for循环怎么写,从上到下,还是从下到上,从左到右还是从右到左
//dp[x][y][step]= // dp[x - 1][ y + 2]+[step - 1] //+ dp[x + 1][ y + 2]+[step - 1] //说明从低层到高层,x y并无讲究
/** * 检查马儿当前位置是否越界 跳出棋盘外 * * @param x 横坐标 * @param y 纵坐标 * @return 是否越界 越界返回false */ private static boolean checkPosition(int x, int y) { return x >= 0 && x <= 8 && y >= 0 && y <= 9; } static class DynamicProgramming { static int getValueOfDpArrayOutBoundReturn0(int[][][] dp, int x, int y, int step) { try { return dp[x][y][step]; } catch (Exception e) { return 0; } } static int horseJumpToTargetPosition(int x, int y, int step) { //目标位置太离谱。需要花完的步数不符合实际 返回0 if (!checkPosition(x, y) || step < 0) { return 0; } int[][][] dp = new int[8 + 1][9 + 1][step + 1]; dp[0][0][0] = 1; for (int curLayer = 1; curLayer <= step; curLayer++) { for (int curX = 0; curX <= 8; curX++) { for (int curY = 0; curY <= 9; curY++) { ///假如当前位置(6,6)依赖于(5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7) //curLayer=6 表示6步到(6,6) 右多少种方法, //方法总数等于 用五步到5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7)存在多少种方法 dp[curX][curY][curLayer] = getValueOfDpArrayOutBoundReturn0(dp, curX - 1, curY + 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 1, curY + 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 2, curY + 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 2, curY - 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 1, curY - 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 1, curY - 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 2, curY - 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 2, curY + 1, curLayer - 1); } } } return dp[x][y][step]; } } -
-
五丶leetcode上的一些动态规划题目
这里就没一步步使用套路来,熟练了就直接可以想到状态转移方程,直接写就完事了
1.[最长回文子串](5. 最长回文子串 - 力扣(Leetcode))
public String longestPalindrome(String s) {
if (s == null || s.length() <= 1) {
return s;
}
int len = s.length();
int maxLen = 1;
int begin = 0;
//dp[i][j] 表示 s[i..j] 是否是回文串
boolean[][] dp = new boolean[len][len];
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
//i=1 j = 3 中间只有一个字符的时候,如果s[i]=s[j]那么必然回文
//dp[i][j] = s[i]==s[j] 且 dp[i+1][j-1]
//也就是说 当前格子依赖于左下方格子,那么填格子使用一列一列的填
for (int j = 1; j < len; j++) {
//当前是第j列,第 i行 判断是否回文
for (int i = 0; i < j; i++) {
boolean charEqual = s.charAt(i) == s.charAt(j);
//dp[3][6] = s[3]==s[6] && dp[4][5];
if (j - i >= 3) {
dp[i][j] = charEqual && dp[i + 1][j - 1];
} else {
//j - i<3 说明中间只有一个 或者 0 个字符 那么直接看s[i],s[j]是否相等
dp[i][j] = charEqual;
}
if (dp[i][j] && maxLen < j - i + 1) {
begin = i;
maxLen = j - i + 1;
}
}
}
return s.substring(begin, begin + maxLen);
}
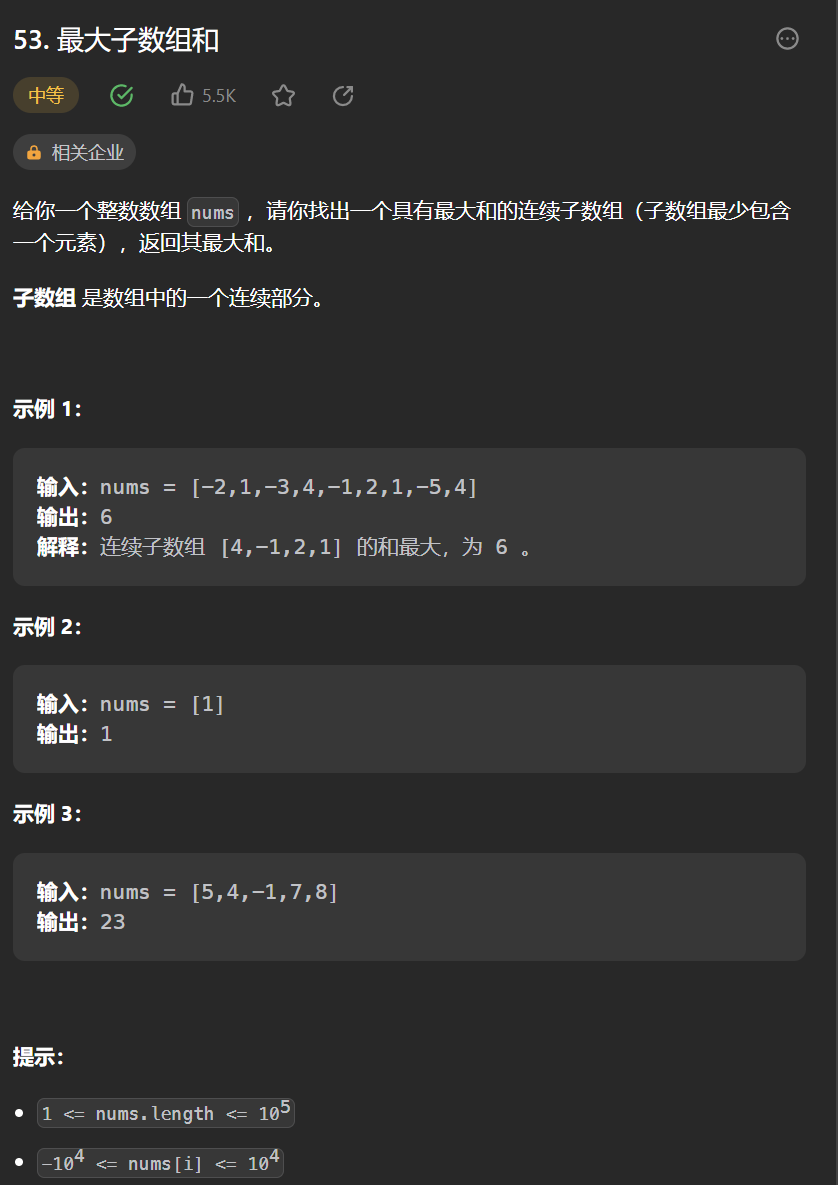
2.[最大子数组和](53. 最大子数组和 - 力扣(Leetcode))
public int maxSubArray1(int[] nums) {
int maxSum = nums[0];
int len = nums.length;
//dp[i] dp[0....i]之间的每一个子数组的,最大子数组和
//dp[i] = max(dp[i-1],dp[i]+nums[i])
int[] dp = new int[len];
dp[0] = nums[0];
for(int i=1; i<len; i++){
dp[i] = Math.max(nums[i]+dp[i-1],nums[i]);
maxSum = Math.max(maxSum,dp[i]);
}
return maxSum;
}
public int maxSubArray(int[] nums) {
int maxSum = nums[0];
int len = nums.length;
int dp = nums[0];
for(int i=1; i<len; i++){
dp = Math.max(nums[i]+dp,nums[i]);
maxSum = Math.max(maxSum,dp);
}
return maxSum;
}
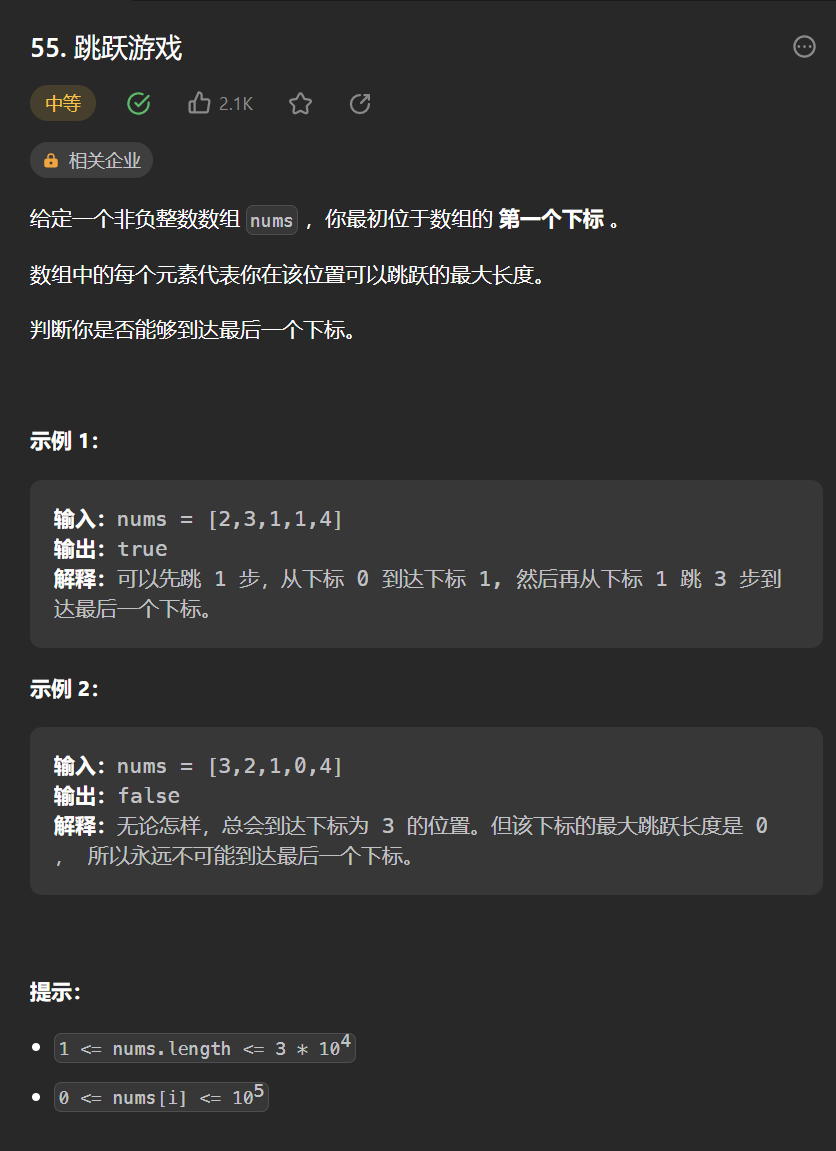
3.[跳跃游戏](55. 跳跃游戏 - 力扣(Leetcode))
public boolean canJump(int[] nums) {
if(nums.length <=1){
return true;
}
//dp[i]表示能否跳到i位置
boolean[] dp = new boolean[nums.length];
dp[0]=true;
dp[1] = dp[0]&&nums[0]>=1;
//当前判断是否可以跳到第i位置
for(int i =2 ;i < nums.length ; i++){
//i位置之前的所有位置遍历判断
//能否从pos 跳到 i位置
for(int pos=0;pos<i;pos++){
//首先如果连pos位置都没办法到达 那么gg 进行下一轮循环
boolean canBePos = dp[pos];
if(!canBePos){
continue;
}
//pos 和i 的距离
int dis = i-pos;
//pos 位置能跳的最大距离是否大于 pos和i的距离
boolean jumpLenBetterDis = nums[pos]>=dis;
//如果可以 那么说明i位置可以到达
if(jumpLenBetterDis){
dp[i]=true;
break;
}
}
}
return dp[nums.length-1];
}
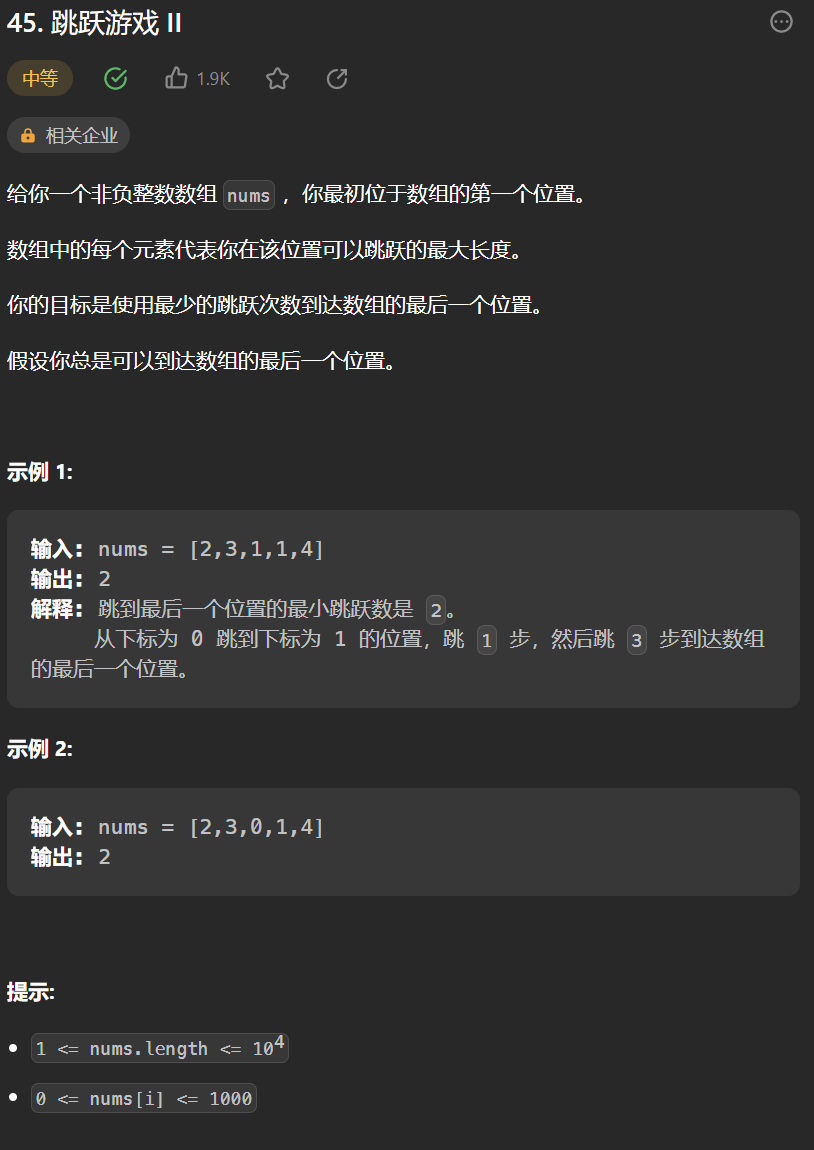
4.[跳跃游戏 II](45. 跳跃游戏 II - 力扣(Leetcode))
class Solution {
public int jump(int[] nums) {
if(nums.length<=1){
return 0;
}
int len = nums.length;
//dp[i]跳到i位置所需要的最西澳部署
int[]dp = new int[nums.length];
dp[0]=0;
dp[1]=1;
//跳到i位置最少的步数
for(int i = 2; i<len; i++){
//从pos 能否跳到i 如果可以那么dp[i] = min(dp[i],dp[pos]+1)
for(int pos = 0;pos<i;pos++){
int maxCanJump = nums[pos];
//可以跳到
if(maxCanJump+pos>=i){
//dp[i]还没有刷新过 那么 直接赋值
if(dp[i] == 0){
dp[i] = dp[pos]+1;
}else{
//取最小
dp[i] = Math.min(dp[pos]+1,dp[i]);
}
}
}
}
return dp[len-1];
}
}
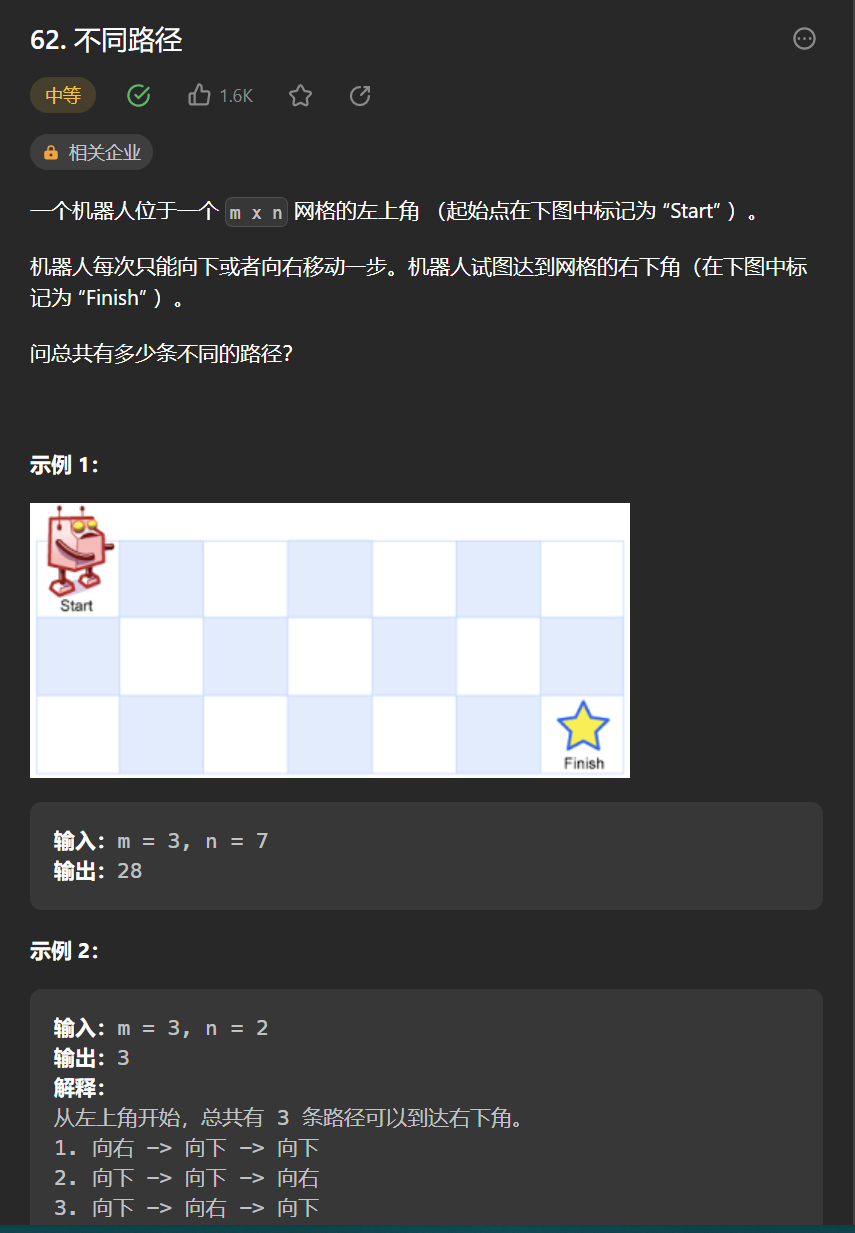
5.[不同路径](62. 不同路径 - 力扣(Leetcode))
class Solution {
public int uniquePaths(int m, int n) {
if(m==1 && n==1){
return 1;
}
//dp[i][j] 表示到i,j位置有多少种走法
//dp[i][j] = dp[i-1][j] dp[i][j-1]
int[][] dp = new int[m][n];
dp[0][0] = 1;
for(int i=0; i<m ;i++){
for(int j=0;j<n;j++){
dp[i][j] += outBoudGet(dp,i-1,j);
dp[i][j] += outBoudGet(dp,i,j-1);
}
}
return dp[m-1][n-1];
}
int outBoudGet(int[][]dp,int i,int j ){
try{
return dp[i][j];
}catch(Exception e){
return 0;
}
}
}
6.[不同路径 II](63. 不同路径 II - 力扣(Leetcode))
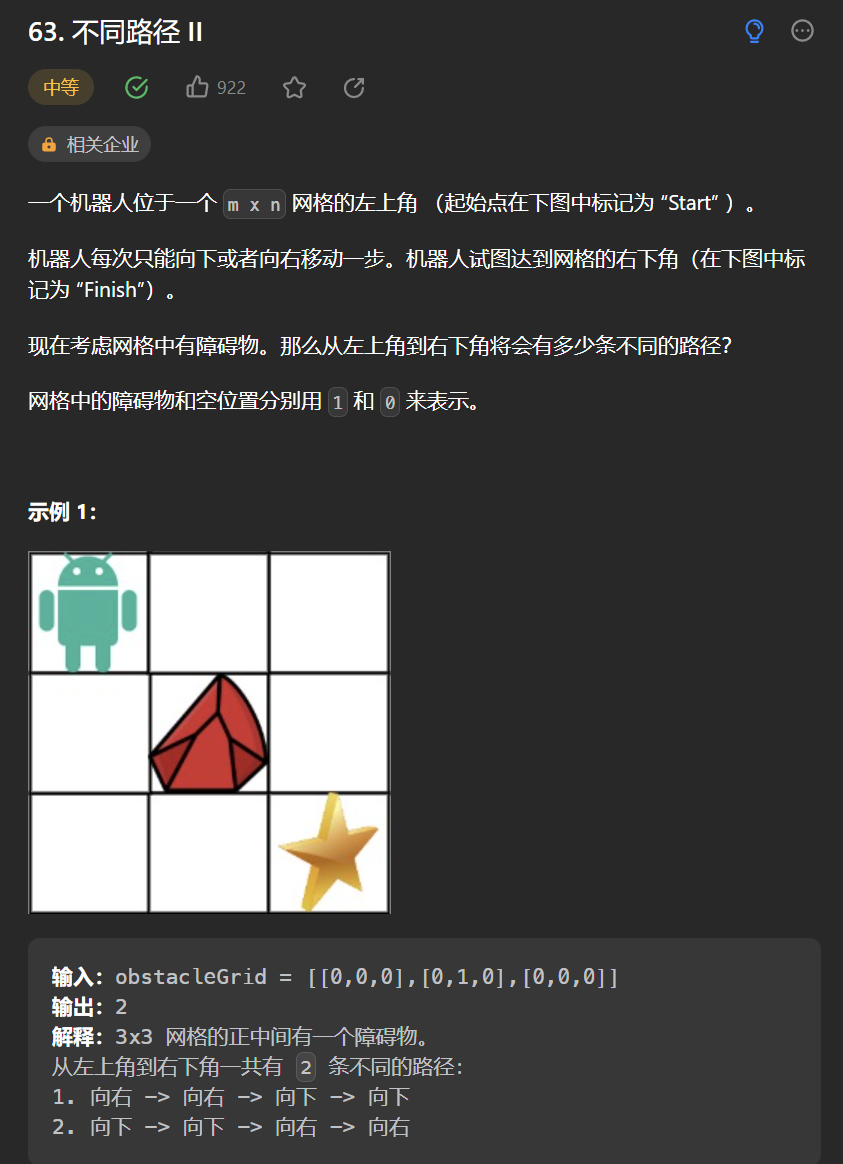
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
if (obstacleGrid[m - 1][n - 1] == 1) {
return 0;
}
//dp[i][j] 表示到i,j位置有多少种走法
//dp[i][j] = dp[i-1][j] dp[i][j-1]
int[][] dp = new int[m][n];
dp[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] += outBoudGet(dp, i - 1, j, obstacleGrid);
dp[i][j] += outBoudGet(dp, i, j - 1, obstacleGrid);
}
}
return dp[m - 1][n - 1];
}
int outBoudGet(int[][] dp, int i, int j, int[][] obstacleGrid) {
try {
if (obstacleGrid[i][j] == 1) {
return 0;
}
return dp[i][j];
} catch (Exception e) {
return 0;
}
}
}
7.[最小路径和](64. 最小路径和 - 力扣(Leetcode))

class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
//dp[i][j]表示走到i,j位置最小的路径和
int[][]dp = new int[m][n];
dp[0][0] = grid[0][0];
for(int i = 0;i<m;i++){
for(int j = 0;j<n;j++){
int rowMinus = Integer.MAX_VALUE;
int colMinus = Integer.MAX_VALUE;
if(i-1>=0){
rowMinus = dp[i-1][j];
}
if(j-1>=0){
colMinus = dp[i][j-1];
}
int min = Math.min(rowMinus,colMinus);
if(min == Integer.MAX_VALUE){
min = 0;
}
dp[i][j] = min + grid[i][j];
}
}
return dp[m-1][n-1];
}
}
8.[买卖股票的最佳时机 II](122. 买卖股票的最佳时机 II - 力扣(Leetcode))
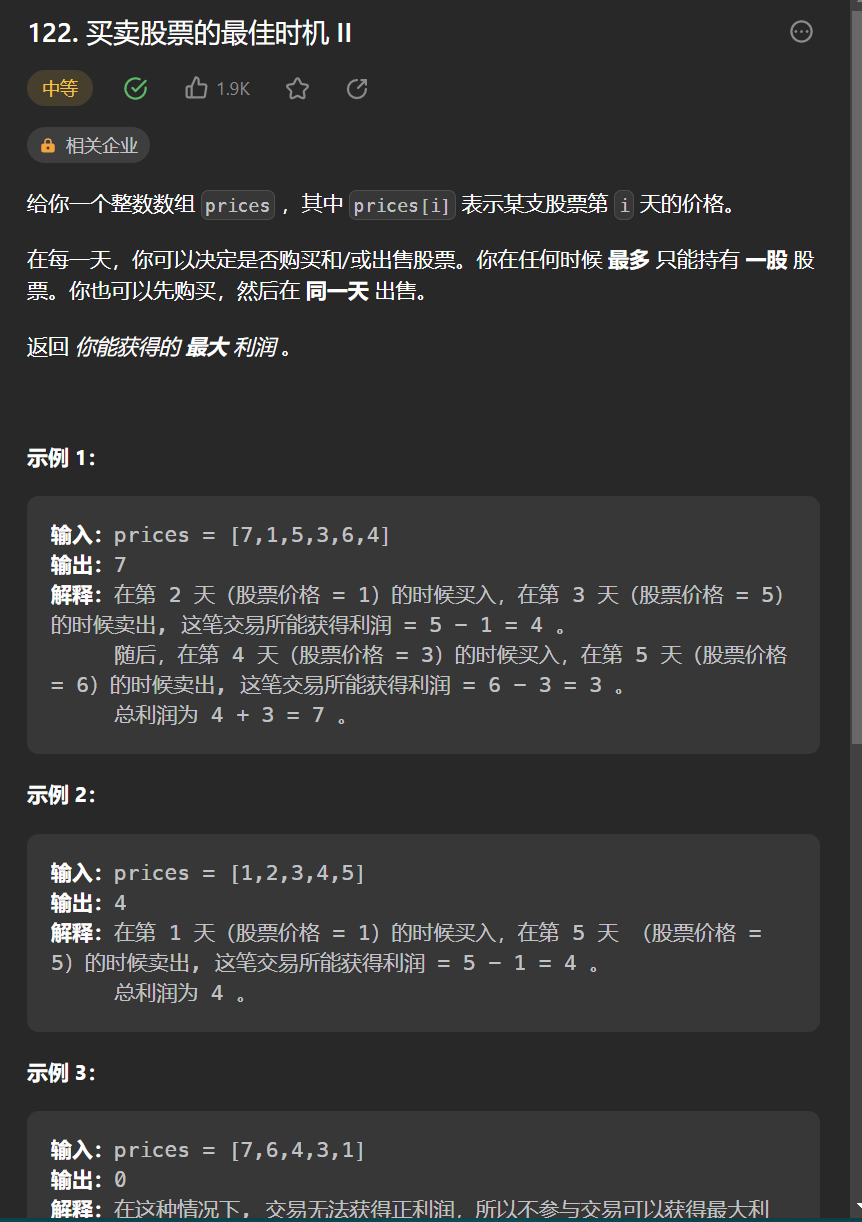
class Solution {
public int maxProfit1(int[] prices) {
int len = prices.length;
if(len<=1){
return 0;
}
//dp[i][0]表示第i+1天不持有股票的收益
//dp[i][1] 表示第i+1天持有当前股票的收益
int [][]dp = new int[len][2];
//第1天 不持有的股票收益,没有机会买,也没股票卖所有为0
dp[0][0] = 0;
//第1天 持有,都没机会卖 那么买入导致收益为负数
dp[0][1] = -prices[0];
//第二天开始
for (int i = 1; i < len; i++) {
//第二天不持有 那么是第一天买然后卖赚 还是 继续持有不买赚
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
//第二天持有,那么是第一天的继续持有赚,还是前一天不买,现在买赚
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];
}
public int maxProfit(int[] prices) {
int len = prices.length;
if(len<=1){
return 0;
}
//第1天 不持有的股票收益,没有机会买,也没股票卖所有为0
int dpNotHold = 0;
//第1天 持有,都没机会卖 那么买入导致收益为负数
int dpHold = -prices[0];
//第二天开始
for (int i = 1; i < len; ++i) {
//第二天不持有 那么是第一天买然后卖赚 还是 继续持有不买赚
int dpNotHoldNew = Math.max(dpNotHold, dpHold + prices[i]);
//第二天持有,那么是第一天的继续持有赚,还是前一天不买,现在买赚
int dpHoldNew = Math.max(dpHold, dpNotHold - prices[i]);
dpNotHold = dpNotHoldNew;
dpHold = dpHoldNew;
}
return dpNotHold;
}
}
9.[单词拆分](139. 单词拆分 - 力扣(Leetcode))
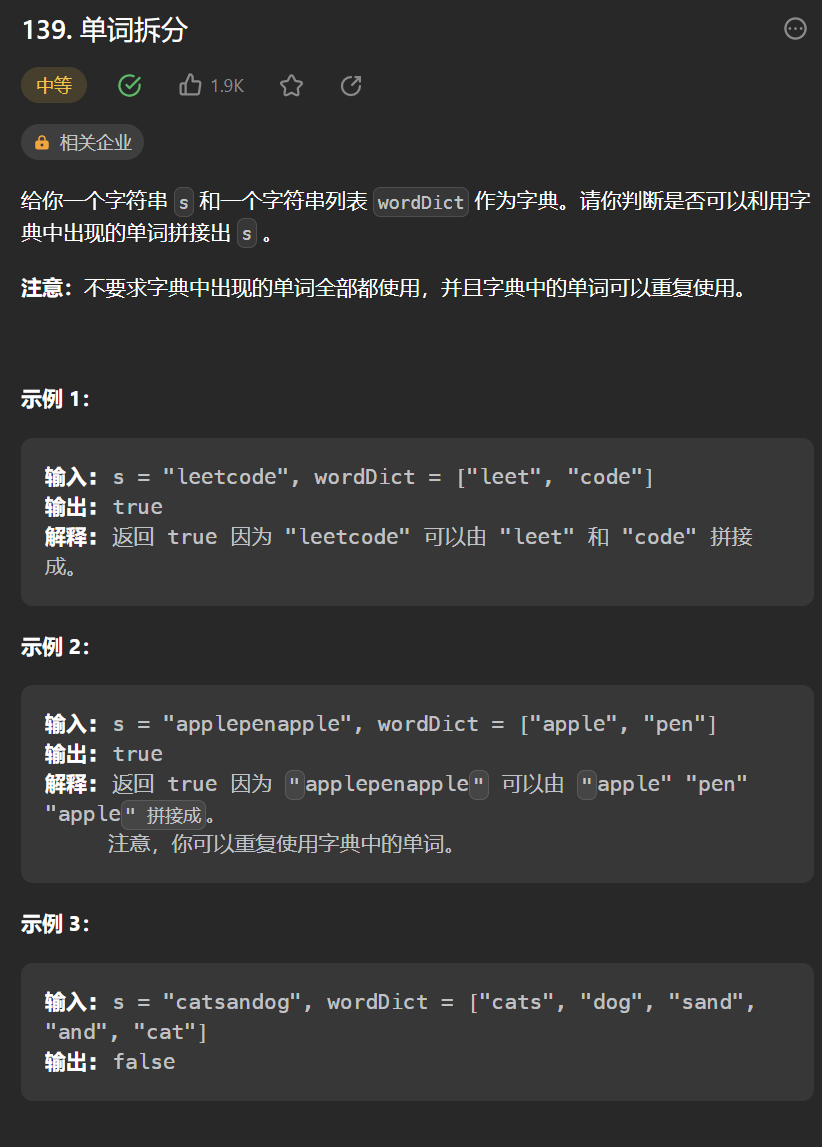
class Solution {
public int maxProduct1(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i结尾的子数组最大值
//dp[i][1]则表示最小值
int[][] dp = new int[len][2];
//初始化自己一个人作为子数组的值
for(int i = 0 ; i < len ; i++){
dp[i][0] = nums[i];
dp[i][1] = nums[i];
}
int maxRes = dp[0][0];
for(int i = 1 ; i < len ; i++){
//以i结尾
int max = Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]);
//和 单独作为子数组取最大
max = Math.max(max,dp[i][0]);
dp[i][0] = max;
maxRes = Math.max(max,maxRes);
int min = Math.min(dp[i-1][1]*nums[i],dp[i-1][0]*nums[i]);
min = Math.min(min,dp[i][1]);
dp[i][1] = min;
}
return maxRes;
}
public int maxProduct(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i结尾的子数组最大值
//dp[i][1]则表示最小值
int maxPre = nums[0];
int minPre = nums[0];
int maxRes = maxPre;
for(int i = 1 ; i < len ; i++){
//以i结尾
int max = Math.max(maxPre*nums[i],minPre*nums[i]);
//和 单独作为子数组取最大
max = Math.max(max,nums[i]);
int min = Math.min(minPre*nums[i],maxPre*nums[i]);
min = Math.min(min,nums[i]);
maxPre = max;
minPre = min;
maxRes = Math.max(max,maxRes);
}
return maxRes;
}
}
152.[乘积最大子数组](152. 乘积最大子数组 - 力扣(Leetcode))
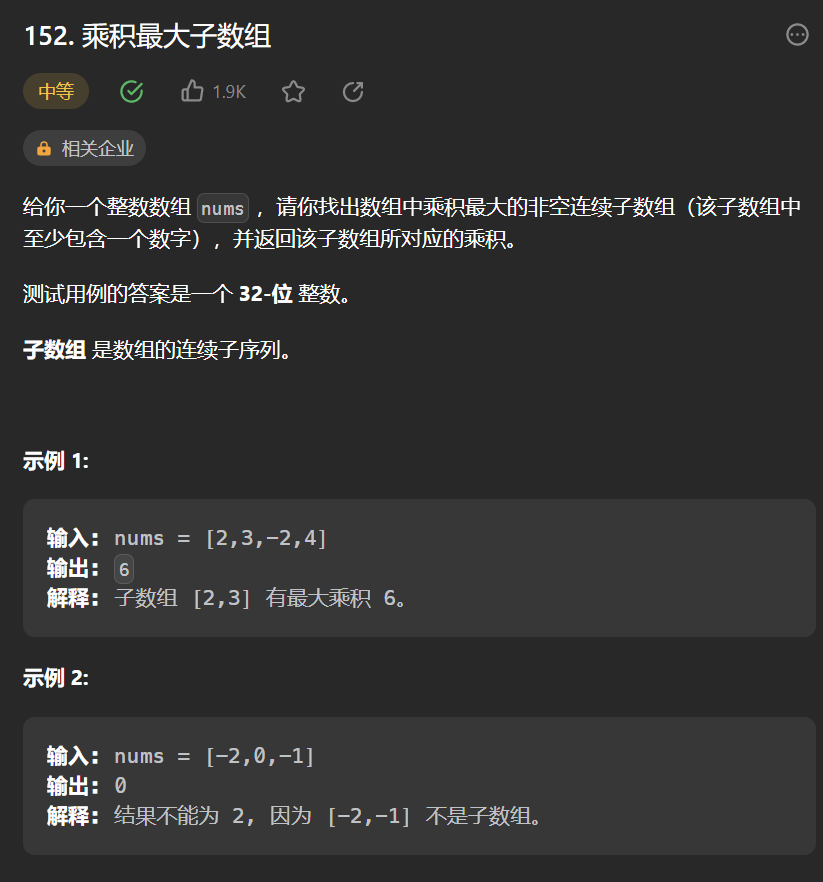
class Solution {
public int maxProduct1(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i结尾的子数组最大值
//dp[i][1]则表示最小值
int[][] dp = new int[len][2];
//初始化自己一个人作为子数组的值
for(int i = 0 ; i < len ; i++){
dp[i][0] = nums[i];
dp[i][1] = nums[i];
}
int maxRes = dp[0][0];
for(int i = 1 ; i < len ; i++){
//以i结尾
int max = Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]);
//和 单独作为子数组取最大
max = Math.max(max,dp[i][0]);
dp[i][0] = max;
maxRes = Math.max(max,maxRes);
int min = Math.min(dp[i-1][1]*nums[i],dp[i-1][0]*nums[i]);
min = Math.min(min,dp[i][1]);
dp[i][1] = min;
}
return maxRes;
}
public int maxProduct(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i结尾的子数组最大值
//dp[i][1]则表示最小值
int maxPre = nums[0];
int minPre = nums[0];
int maxRes = maxPre;
for(int i = 1 ; i < len ; i++){
//以i结尾
int max = Math.max(maxPre*nums[i],minPre*nums[i]);
//和 单独作为子数组取最大
max = Math.max(max,nums[i]);
int min = Math.min(minPre*nums[i],maxPre*nums[i]);
min = Math.min(min,nums[i]);
maxPre = max;
minPre = min;
maxRes = Math.max(max,maxRes);
}
return maxRes;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号