【数据结构】3、hashmap=》tableSizeFor 中求大于等于当前数的最小2的幂

 

最近面试被问到hashmap的实现，因为前段时间刚好看过源码，显得有点信心满满，但是一顿操作下来的结论是基础不够扎实。。。

好吧，因为我开始看hashmap是想了解这到底是一个什么样的机制，具体有啥作用，并没有过于细节去了解，所以问到细节的地方就难免漏洞百出，

回来之后，决定吧容器类的实现原理，去专研一下，目的是为了以后写代码自己可以去优化它

 

好了，不BB了，直接上代码，hashmap中有这么一段代码

//容器最大容量
    static final int MAXIMUM_CAPACITY = 1 << 30;

    /**
     *
     * @program: y2019.collection.MyHashMap
     * @description: 这个方法用于找到大于等于initialCapacity的最小的2的幂（initialCapacity如果就是2的幂，则返回的还是这个数）。
     * @auther: xiaof
     * 总结：
     * 1.说白了就是为了保证所有的位数（二进制）都是1，那么就可以保证这个数就是2的幂
     * 2.不断做无符号右移，是为了吧高位的数据拉下来做或操作，来保证对应的底位都是1
     * @date: 2019/6/25 10:25
     */
    public static final int tableSizeFor(int cap) {
        //这是为了防止，cap已经是2的幂。如果cap已经是2的幂
        int n = cap - 1;
        //第一次右移，由于n不等于0（如果为0，不管几次右移都是0，那么最后有个n+1的操作），则n的二进制表示中总会有一bit为1
        //这里无符号右移一位之后做或操作，那么会导致原来有1的地方紧接着也是1
        //比如00000011xxxxxxxx
        //还有一点无符号右移是为了避免前位补1，导致数据溢出，因为负数是以补码的形式存在的，那么就会再高位补1
        n |= n >>> 1;
        //第二次无符号右移，并做或操作
        //00000011xxxxxxxx=>0000001111xxxxxx 这个时候就是4个1
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        //由于int最大也就是2的16次幂，所以到16停止
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

 

我开始的不明白的地方是为什么要做4次右移？？？为什么要做无符号右移？？？

那么我手动时间一个low点的版本我们对比一下

public static final int tableSizeFor2(int cap) {
        //这是为了防止，cap已经是2的幂。如果cap已经是2的幂
        int n = cap - 1;
        n |= n & 0xffff;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

原谅我的无知，我的第一反应就是这个，想都没想为什么不这样做。。。

结果发现相差甚远

 

第三行就是我这第二个方法得到的值，除了吧负数排除之外，没啥屌用，就是把原来的n去掉符号之后做了一次与运算

 

 这个题的原理是获取到这个入参的位数，然后获取2的N次幂

public static final int tableSizeFor3(int cap) {
        //这是为了防止，cap已经是2的幂。如果cap已经是2的幂
        int n = (cap - 1) & 0xffff;
        String hex = Integer.toBinaryString(n);
        return (cap <= 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : (int) Math.pow(2, hex.length());
    }

 

我们再这样处理

 

我们发现好像很接近了，我们发现n为1的时候，我们得到的长度是2，如果是以大于等于这个数的2的N次幂的话，我觉得我下面这个方法视乎更符合要求

 

 

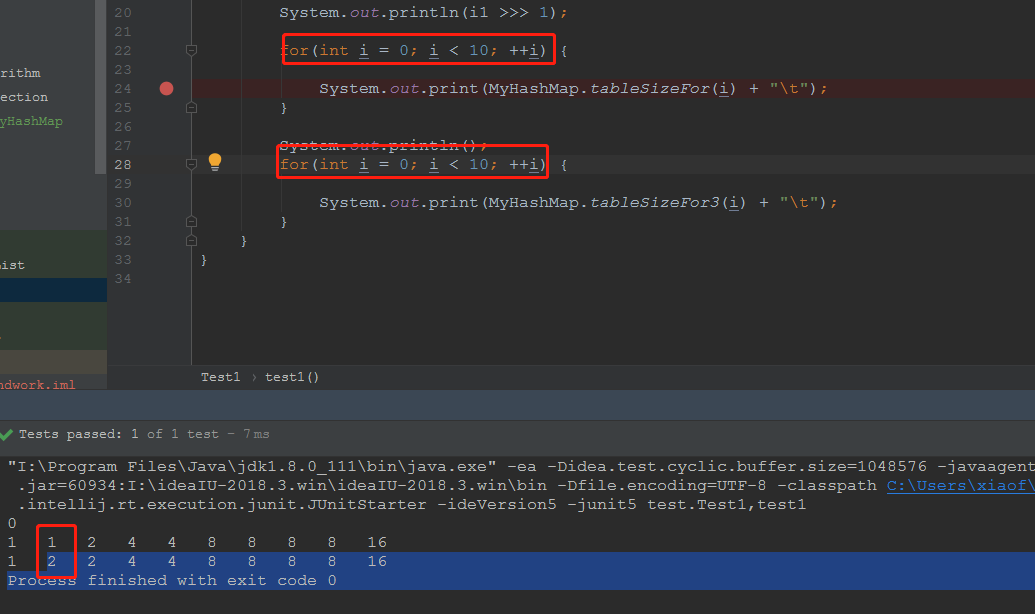
 接下来我们来试试性能？

 当我们需要计算的数量达到1000000的时候，我们发现，这两个操作的性能相差有点大。。。

 

 

 

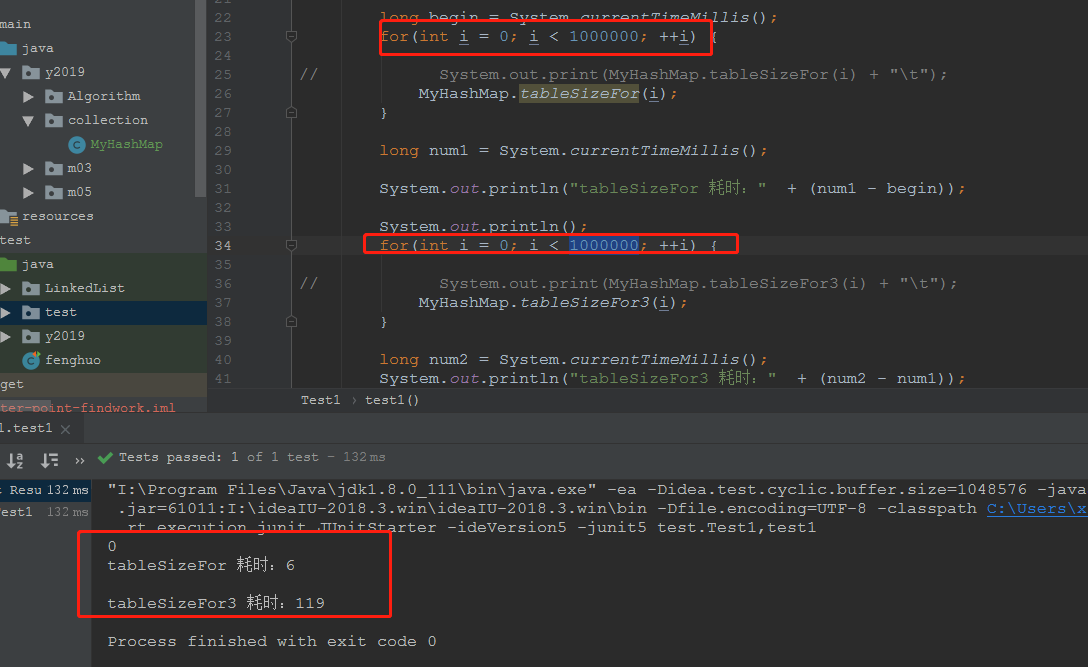
 好吧，结论发现就是，jdk的源码不亏是经过千锤百炼的，一些看不懂的操作也许就是故意而为！！！

多关注这些看不懂的操作，学会了你也是大神！！！

 

参考文章：

https://blog.csdn.net/fan2012huan/article/details/51097331