地球轨道计算方法,开普勒三大定律的证明,补充-解析几何之椭圆
http://math.sjtu.edu.cn/jidi/sxsy/
开普勒三大定律的证明
http://zh.wikipedia.org/wiki/%E5%BC%80%E6%99%AE%E5%8B%92%E5%AE%9A%E5%BE%8B#.E5.BC.80.E6.99.AE.E5.8B.92.E7.AC.AC.E4.B8.89.E5.AE.9A.E5.BE.8B
开普勒定律
维基百科,自由的百科全书
开普勒定律是开普勒发现的关于行星运动的定律。他於1609年在他出版的《新天文学》上发表了关于行星运动的两条定律,又於1618年,发现了第三条定律。
开普勒很幸运地能够得到,著名的丹麦天文学家第谷·布拉赫所观察与收集的,非常精确的天文資料。大约于 1605 年,根据布拉赫的行星位置資料,开普勒发现行星的移动遵守三条相当简单的定律。
开普勒的定律给予亚里士多德派与托勒密派在天文学与物理学上极大的挑战。他主张地球是不斷地移动的;行星轨道不是周转圆 (epicycle 的,而是椭圆形的;行星公转的速度不等恒。这些论点,大大地动摇了当时的天文学与物理学。经过了几乎一世纪披星戴月,废寝忘食的研究,物理学家终于能够用物理理论解释其中的道理。牛顿利用他的第二定律和万有引力定律,在数学上严格地証明开普勒定律,也让人们了解其中的物理意义。
目录[隐藏] |
[编辑] 开普勒定律
开普勒的三条行星运动定律改变了整个天文学,彻底摧毁了托勒密复杂的宇宙体系,完善并简化了哥白尼的日心说。
[编辑] 开普勒第一定律
开普勒第一定律,也称椭圆定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。
[编辑] 开普勒第二定律
开普勒第二定律,也称面积定律:在相等时间内,太阳和运动着的行星的连线所扫过的面积都是相等的。
这一定律实际揭示了行星绕太阳公转的角动量守恒。用公式表示为
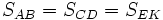 。
。
[编辑] 开普勒第三定律
开普勒第三定律,也称调和定律:各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。
由这一定律不难导出:行星与太阳之间的引力与半径的平方成反比。这是牛顿的万有引力定律的一个重要基础。
用公式表示为
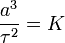 ;
;
这里, 是行星公转轨道半长轴,
是行星公转轨道半长轴, 是行星公转周期,
是行星公转周期,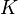 是常数。
是常数。
[编辑] 数学导引
开普勒定律是关于行星环绕太阳的运动,而牛顿定律更广义的是关于几个粒子因万有引力相互吸引而产生的运动。在只有两个粒子,其中一个粒子超轻于另外 一个粒子,这些特别状况下,轻的粒子会环绕重的粒子移动,就好似行星根据开普勒定律环绕太阳的移动。然而牛顿定律还容许其它解答,行星轨道可以呈抛物线运动或双曲线运动。这是开普勒定律无法预测到的。在一个粒子并不超轻于另外一个粒子的状况下,依照广义二体问题的解答,每一个粒子环绕它们的共同质心移动。这也是开普勒定律无法预测到的。
开普勒定律,或者是用几何语言,或者是用方程式,将行星的坐标及时间跟轨道参数相连结。牛顿第二定律是一个微分方程式。开普勒定律的导引涉及解微分方程式的艺术。我们会先导引开普勒第二定律,因为开普勒第一定律的导引必须建立于开普勒第二定律。
[编辑] 开普勒第二定律导引
牛顿万有引力定律阐明:任意两个粒子由通过连线方向的力相互吸引。该引力的的大小与它们的质量乘积成正比,与它们距离的平方成反比。由于太阳超重于行星,我们可以假设太阳是固定的。用方程式表示,
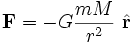 ;
;
这里,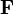 是太阳作用於行星的万有引力、
是太阳作用於行星的万有引力、 是行星的质量、
是行星的质量、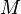 是太阳的质量、
是太阳的质量、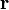 是行星相对于太阳的位移向量、
是行星相对于太阳的位移向量、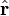 是
是 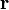 的单位向量。
的单位向量。
牛顿第二定律声明:物體受力後所产生的加速度 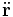 ,和其所受的淨力
,和其所受的淨力 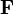 成正比,和其質量
成正比,和其質量  成反比。用方程式表示,
成反比。用方程式表示,
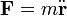 。
。
合并这两个方程式,
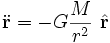 。 (1)
。 (1)
思考位置向量  ,随时间
,随时间 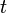 微分一次可得到速度向量,再微分一次则可得到加速度向量:
微分一次可得到速度向量,再微分一次则可得到加速度向量:
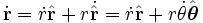 ,
,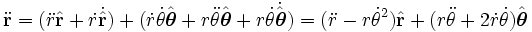 。(2)
。(2)
在这里,我们用到了单位向量微分方程式:
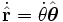 ,
,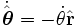 。
。
合并方程式 (1) 与 (2) ,可以得到向量运动方程式:
取各个分量,我们得到两个常微分方程式,一个是关于径向加速度,另一个是关于切向加速度:
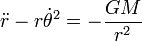 ,(3)
,(3)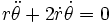 。(4)
。(4)
导引开普勒第二定律只需切向加速度方程式。试想行星的角动量  。由于行星的质量是常数,角动量随时间的导数为
。由于行星的质量是常数,角动量随时间的导数为
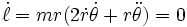 。
。
角动量  也是一个运动常数,即使距离
也是一个运动常数,即使距离  与角速度
与角速度 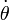 都可能会随时间变化。
都可能会随时间变化。
从时间 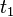 到时间
到时间  扫过的区域
扫过的区域 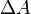 ,
,
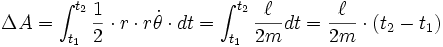 。
。
行星太阳连线扫过的区域面积相依于间隔时间  。所以,开普勒第二定律是正确的。
。所以,开普勒第二定律是正确的。
[编辑] 开普勒第一定律导引
设定 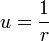 。这样,角速度是
。这样,角速度是
 。
。
随时间微分与随角度微分的关系为
 。
。
随时间微分徑向距離 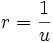 :
:
 。
。
再微分一次:
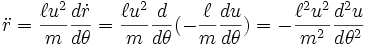 。
。
代入径向运动方程式 (3) ,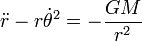 ,
,
 。
。
将此方程式除以 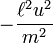 ,则可得到一个简单的常係数非齐次线性全微分方程式来描述行星轨道:
,则可得到一个简单的常係数非齐次线性全微分方程式来描述行星轨道:
 。
。
特征方程式为
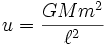 。
。
求解剩馀的常係数齐次线性全微分方程式,
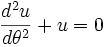 。
。
其特解方程式为
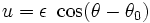 ;
;
这里, 与
与 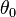 都是任意积分常数。综合特征方程式与特解方程式,
都是任意积分常数。综合特征方程式与特解方程式,
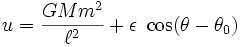 。
。
选择坐标轴,让 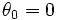 。代回
。代回 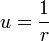 ,
,
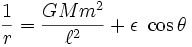 。
。
假若 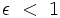 ,则
,则  所描述的是椭圆轨道。所以,开普勒第一定律是正确的。
所描述的是椭圆轨道。所以,开普勒第一定律是正确的。
[编辑] 开普勒第三定律导引
在建立牛顿万有引力定律的概念与数学架构上,开普勒第三定律是牛顿依据的重要线索之一。假若我们接受牛顿运动定律。试想一个虚拟行星环绕着太阳公转,行星的移动轨道恰巧呈圆形,轨道半径为  。那末,太阳作用于行星的万有引力为
。那末,太阳作用于行星的万有引力为 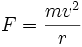 。行星移动速度为
。行星移动速度为 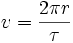 。依照开普勒第三定律,这速度
。依照开普勒第三定律,这速度 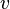 与半径的平方根
与半径的平方根  成反比。所以,万有引力
成反比。所以,万有引力 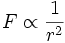 。猜想这大概是牛顿发现万有引力定律的思路,虽然我们并不能完全确定,因为我们无法在他的计算本裡,找到任何关于这方面的证据。
。猜想这大概是牛顿发现万有引力定律的思路,虽然我们并不能完全确定,因为我们无法在他的计算本裡,找到任何关于这方面的证据。
开普勒第一定律阐明,行星环绕太阳的轨道是椭圆形的。椭圆的面积是 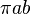 ;这里,
;这里, 与
与 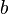 分别为椭圆的半長軸与半短軸。在开普勒第二定律导引里,行星-太阳连线扫过区域速度
分别为椭圆的半長軸与半短軸。在开普勒第二定律导引里,行星-太阳连线扫过区域速度 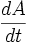 为
为
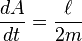 。
。
所以,行星公转周期  为
为
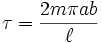 。(5)
。(5)
关于此行星环绕太阳,椭圆的半長軸  ,半短軸
,半短軸 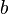 与近拱距
与近拱距 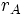 (近拱点 A 与引力中心之间的距离),远拱距
(近拱点 A 与引力中心之间的距离),远拱距  (远拱点 B 与引力中心之间的距离)的关系分别为
(远拱点 B 与引力中心之间的距离)的关系分别为
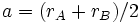 ,(6)
,(6)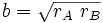 。(7)
。(7)
如果想要知道半長軸与半短軸,必须先求得近拱距与远拱距。依据能量守恒定律,
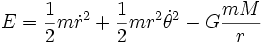 。
。
在近拱点 A 与远拱点 B,径向速度都等于零:
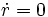 。
。
所以,
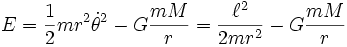 。
。
稍为加以编排,可以得到  的一元二次方程式:
的一元二次方程式:
 。
。
其兩個根分别为椭圆轨道的近拱距 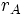 与远拱距
与远拱距  。
。
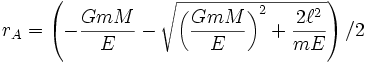 ;
; 。
。
代入方程式 (6) 与 (7) ,
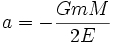 ,
,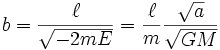 。
。
代入方程式 (5) ,周期的方程式为
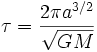 。
。
椭圆
维基百科,自由的百科全书
在数学中,椭圆是平面上到两个固定点的距离之和是常数的轨迹。这两个固定点叫做焦点。
经由这个定义,这样画出一个椭圆:先准备一条线,将这条线的两端各绑在一点上(这两个点就当作是椭圆的两个焦点);取一支笔,将线绷紧,这时候两个点和笔就形成了一个三角形;然后拉着线开始作图,持续的使线绷紧,最后就可以完成一个椭圆的图形了。
[编辑] 概述
椭圆是一种圆锥曲线: 如果一个平面切截一个圆锥面,且不与它的底面相交,也不与它的底面平行,则圆锥和平面交截线是个椭圆。
使得 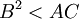 ,这里的系数都是实数,并存在定义在椭圆上的点对 (x, y) 的多于一个的解。
,这里的系数都是实数,并存在定义在椭圆上的点对 (x, y) 的多于一个的解。
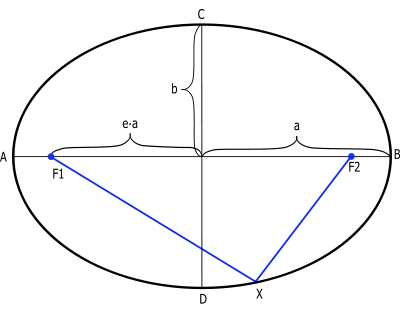
穿过两焦点并终止于椭圆上的线段 AB 叫做长轴。长轴是通过连接椭圆上的两个点所能获得的最长线段。穿过中心(两焦点的中点)垂直于长轴并且终止于椭圆的线段 CD 叫做短轴。半长轴(图中指示为 a)是长轴的一半: 从中心通过一个焦点到椭圆的边缘的线段。类似的,半短轴(图中指示为 b)是短轴的一半。
如果两个焦点重合,则这个椭圆是圆;换句话说,圆是离心率为零的椭圆的特殊情况。
中心位于原点的椭圆  可以被看作单位圆在关联于对称矩阵
可以被看作单位圆在关联于对称矩阵 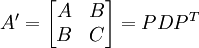 的线性映射下的图像,这里的 D 是带有
的线性映射下的图像,这里的 D 是带有 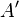 的特征值的对角矩阵,二者沿着主对角线都是正实数的,而 P 是拥有
的特征值的对角矩阵,二者沿着主对角线都是正实数的,而 P 是拥有 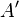 的特征向量作为纵列的实数的酉矩阵。椭圆的长短轴分别沿着
的特征向量作为纵列的实数的酉矩阵。椭圆的长短轴分别沿着 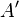 的两个特征向量的方向,而两个与之对应的特征值分别是半长轴和半短轴的长度的平方的倒数。
的两个特征向量的方向,而两个与之对应的特征值分别是半长轴和半短轴的长度的平方的倒数。
椭圆可以通过对一个圆的所有点的 x 坐标乘以一个常数而不改变 y 坐标来生成。
[编辑] 离心率
椭圆的形状可以用叫做椭圆的离心率的一个数来表达,习惯上指示为  。离心率是小于 1 大于等于 0 的正数。离心率 0 表示着两个焦点重合而这个椭圆是圆。
。离心率是小于 1 大于等于 0 的正数。离心率 0 表示着两个焦点重合而这个椭圆是圆。
对于有半长轴 a 和半短轴 b 的椭圆,离心率是
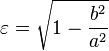 .
.
离心率越大,a 与 b 的比率就越大,因此椭圆被更加拉长。
如果 c 等于从中心到任一焦点的距离,则
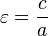 .
.
距离 c 叫做椭圆的线性离心率。在两个焦点间的距离是 2aε。
[编辑] 方程
中心位于点 (h,k) 的主轴平行于 x 轴的椭圆由如下方程指定
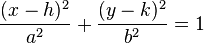 .
.
这个椭圆可以参数化表达为
这里的 t 可以限制于区间  。
。
如果 h = 0 且 k = 0 (就是说,如果中心是原点(0,0)),则
用极坐标可表达为
这里的  是椭圆的离心率。
是椭圆的离心率。
有一个焦点在原点的椭圆的极坐标方程是
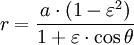 .
.
[编辑] 半正焦弦和极坐标
椭圆的半正焦弦,通常指示为 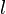 ),是从椭圆的一个焦点到椭圆自身,沿着垂直主轴的直线测量的距离。它有关于
),是从椭圆的一个焦点到椭圆自身,沿着垂直主轴的直线测量的距离。它有关于  和
和 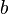 (椭圆的半轴),通过公式
(椭圆的半轴),通过公式 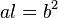 或者如果使用离心率的话
或者如果使用离心率的话  。
。
在极坐标中,一个焦点在原点而另一个焦点在负 x 轴上的椭圆给出自方程
椭圆可以被看作是圆的投影: 在与水平面有角度 φ 的平面上的圆垂直投影到水平面上给出离心率 sin φ 的椭圆,假定 φ 不是 90°。
[编辑] 面积和周长
椭圆所包围的面积是 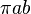 ,这里的 'a' 和 'b' 是半长轴和半短轴。在圆的情况下 a = b,表达式简化为 πa2。
,这里的 'a' 和 'b' 是半长轴和半短轴。在圆的情况下 a = b,表达式简化为 πa2。
椭圆的周长是 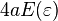 ,这里的函数 E 是第二类完全椭圆积分。
,这里的函数 E 是第二类完全椭圆积分。
精确的无穷级数为:
或:
一个好的近似是拉马努金的:
它还可以写为:
[编辑] 标准方程的推导
假设(注意所有假设只是为了导出椭圆方程时比较简便)动点为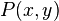 ,两个定点为
,两个定点为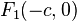 和
和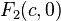 ,则根据定义,动点P的轨迹方程满足(定义式):
,则根据定义,动点P的轨迹方程满足(定义式):
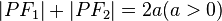 ,其中
,其中 为定长。
为定长。
用两点的距离公式可得: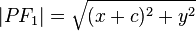 ,
,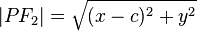 ,代入定义式中,得:
,代入定义式中,得:
整理上式,并化简,得:
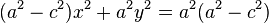 ①
①
当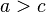 时,并设
时,并设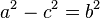 ,则①式可以进一步化简:
,则①式可以进一步化简:
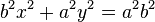 ②
②
因为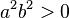 ,将②式两边同除以
,将②式两边同除以 ,可得:
,可得:
则该方程即动点P的轨迹方程,即椭圆的方程。这个形式也是椭圆的标准方程。
- 在方程中,所设的
 称为长轴长,
称为长轴长, 称为短轴长,而所设的定点称为焦点,那么
称为短轴长,而所设的定点称为焦点,那么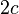 称为焦距。在假设的过程中,假设了
称为焦距。在假设的过程中,假设了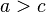 ,如果不这样假设,会发现得不到椭圆。当
,如果不这样假设,会发现得不到椭圆。当 时,这个动点的轨迹是一个线段;当
时,这个动点的轨迹是一个线段;当 时,根本得不到实际存在的轨迹,而这时,其轨迹称为虚椭圆。另外还要注意,在假设中,还有一处:
时,根本得不到实际存在的轨迹,而这时,其轨迹称为虚椭圆。另外还要注意,在假设中,还有一处: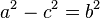 。
。 - 通常认为圆是椭圆的一种特殊情况。
[编辑] 椭圆的旋转和平移
对于平面上任意椭圆 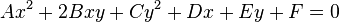 ,我们总可以将之转化为
,我们总可以将之转化为
的形式。具体步骤为,将后式的各乘积乘方项展开,根据与前式对应项系数相等的法则便可求得u,v,f的值。其中,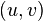 便是该椭圆的中心。
便是该椭圆的中心。
若将
带入式中便可得到平移前的椭圆。
若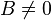 ,则表示椭圆的长短轴与坐标系的坐标轴并不平行或垂直,即发生了旋转。设旋转的角度为
,则表示椭圆的长短轴与坐标系的坐标轴并不平行或垂直,即发生了旋转。设旋转的角度为 , 则有
, 则有
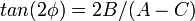 当A-C=0,则说明
当A-C=0,则说明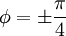
若将
带入式中便可得到旋转前的椭圆。
[编辑] 参见
[编辑] 外部链接
| 隐藏▲
|
|
|---|---|
| 点和线 | 顶点 | 线段 | 直线 | 平行 | 垂直 | 切线 | 法线 | 曲线 | 圆锥曲线 | 双曲线 | 抛物线 | 螺线 | 边 | 周界 | 弦 |
| 平面图形 | 圆 | 椭圆 | 扇形 | 弓形 | 多边形 | 三角形 | 四边形 | 五边形 | 六边形 | 梯形 | 平行四边形 | 菱形 | 矩形 | 正方形 | 鹞形 |
| 立体图形 | 多面体 | 正多面体 | 长方体 | 立方体 | 圆柱体 | 四面体 | 平行六面体 | 棱柱 | 反棱柱 | 棱锥 | 圆锥 | 球体 | 抛物面 | 椭球 | 双曲面 | 圆台 |
| 图形关系 | 相似 | 全等 | 对称 | 平行 | 垂直 | 相邻 | 相交 | 相切 | 镜像 | 旋转 |
| 三角形关系 | 相似三角形 | 全等三角形 |
| 量 | 距离 | 长度 | 周长 | 高度 | 面积 | 表面积 | 体积 | 角度 |
| 比例 | 角 | 圆周率 | 倍数 | 分数 |
| 作图 | 尺子(直尺) | 圆规 | 尺规作图 |
| 理论 | 定理 | 公理 | 定义 | 证明 |



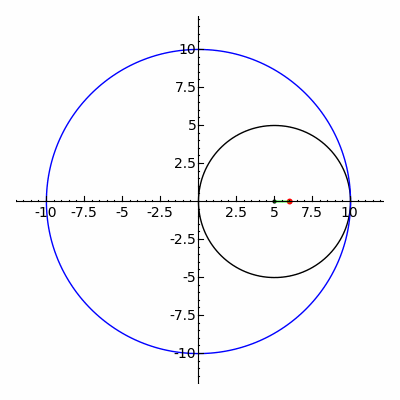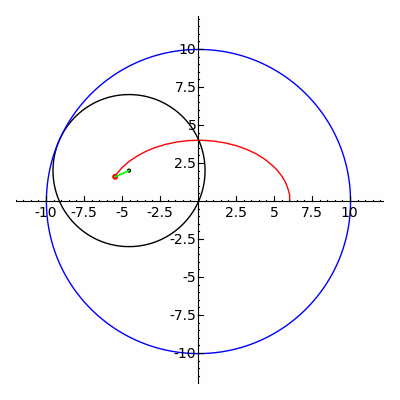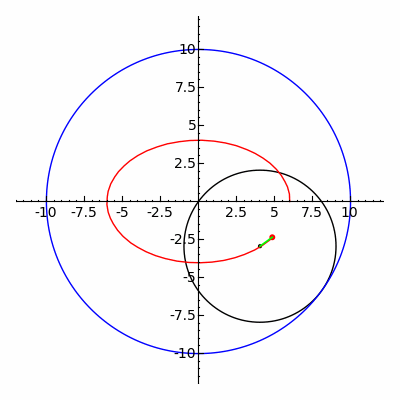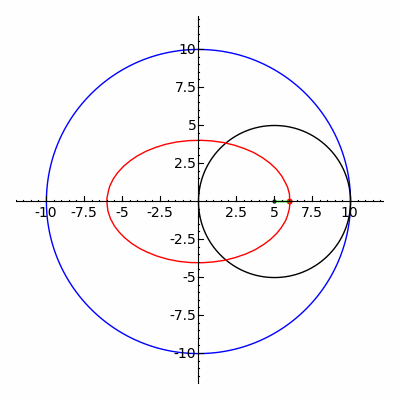
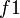 与
与 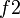 ,第二个行星的椭圆轨道焦点是
,第二个行星的椭圆轨道焦点是  。太阳的位置是在点
。太阳的位置是在点 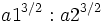 ;这里,
;这里,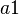 与
与 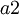 分别为第一个行星与第二个行星的半长轴长度。
分别为第一个行星与第二个行星的半长轴长度。


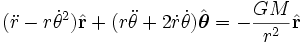

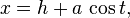
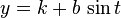
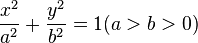
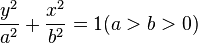


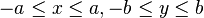



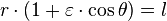
![C = 2\pi a \left[{1 - \left({1\over 2}\right)^2\varepsilon^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{\varepsilon^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{\varepsilon^6\over5} - \dots}\right]\!\,](http://upload.wikimedia.org/math/3/3/3/333f234c62272b2509a5cfb3071d4309.png)
![C = 2\pi a \sum_{n=0}^\infty {\left\lbrace - \left[\prod_{m=1}^n \left({ 2m-1 \over 2m}\right)\right]^2 {\varepsilon^{2n}\over 2n - 1}\right\rbrace}](http://upload.wikimedia.org/math/9/7/3/973e9f2eff62965881fc2d40512412ca.png)
![C \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/math/6/a/e/6ae2da9bd47bab3bde7713c60a04c1bc.png)
![C \approx \pi a \left[ 3 (1+\sqrt{1-\varepsilon^2}) - \sqrt{(3+ \sqrt{1-\varepsilon^2})(1+3 \sqrt{1-\varepsilon^2})} \right] \!\,](http://upload.wikimedia.org/math/d/0/b/d0b466ba8cce6d96a09ba6dfa3e719a3.png)
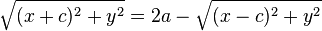
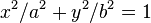
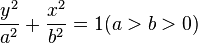
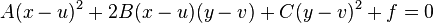
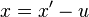
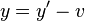
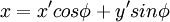
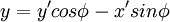



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 字符编码:从基础到乱码解决