数论分块之整除连加和
学过c++的小朋友们都知道
当有整形数字a,b,此时a/b是取整除结果的
例如a=10,b=4,此时a/b=2
现在给你一个数字N
希望你求出N/1,N/2.............N/N的总和
Format
Input
一行给出数字N
N<=1e12
Output
如题
Samples
输入数据 1
3
输出数据 1
5
Hint 3/1+3/2+3/3=3+1+1=5
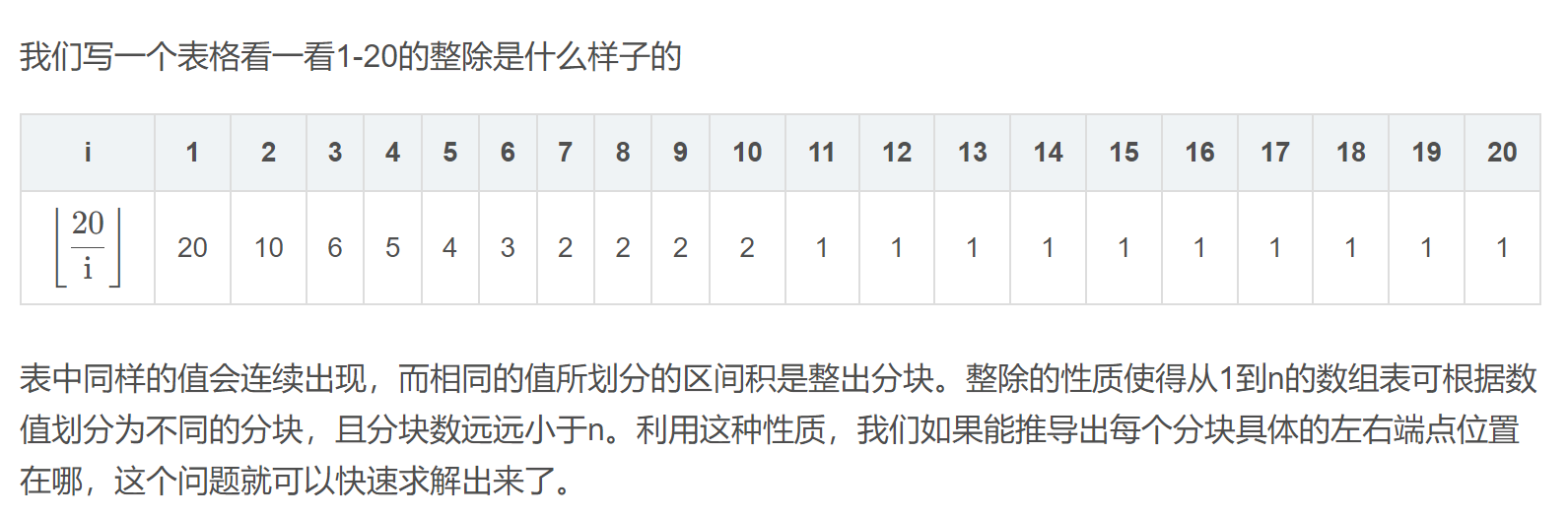
表中同样的值会连续出现,而相同的值所划分的区间积是整除分块。
整除的性质使得从1到n的数组表可根据数值划分为不同的分块,且分块数远远小于n。
利用这种性质,我们如果能推导出每个分块具体的左右端点位置在哪,这个问题就可以快速求解出来了。
假设我们已知某一个分块的左端点L,要求解出该分块的右端点R。
设该分块的数值为K ,则k = ⌊ n/ L ⌋
由于区间[L,R]中每个数字i都满足⌊ n/ i ⌋=k
于是右边界R,即为满足条件i*K<=N中最大的i
即R=⌊ n/ k ⌋=⌊ n/ (⌊ n/ L ⌋) ⌋
例如n=20时
当L=1,求出R=1
当L=2,R=2
当L=3,R=3
.................
当L=7,R=10
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n,l=1,r=0,ans=0;
cin>>n;
while(l<=n){
r=n/(n/l);
ans+=(r-l+1)*(n/l);
l=r+1;
}
cout<<ans;
}
给出正整数n和k,计算j(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值
其中k mod i表示k除以i的余数。
例如j(5, 3)=3 mod 1 + 3 mod 2 + 3 mod 3 + 3 mod 4 + 3 mod 5=0+1+0+3+3=7
Input
输入仅一行,包含两个整数n, k。
1<=n ,k<=10^9
Output
输出仅一行,即j(n, k)。
Sample Input
5 3
Sample Output
7

.
#include <cstdio>
long long n, m, ans;
long long min(long long x, long long y) {
return x < y ? x : y;
}
int main() {
scanf("%lld %lld", &n, &m), ans = n * m;
for (int i = 1, j; i <= n; i = j + 1)
{
if (m/i)
j=min(m / (m / i), n);
else
j=n;
ans -= (m / i) * (i + j) * (j - i + 1) / 2;
}
printf("%lld\n", ans);
return 0;
}
k%i=k-trunc(k/i)*i,当n>k时,直接把长度为(n-k)的区间长度乘以k加入答案,
然后就处理i≤k的时候就可以了,然后就用j=n/(n/i)直接跳到(k/i都相等)区间末尾,
然后需要对这个区间的等差数列求和加入答案,输出即可。。
注意点:输出%lld,加入答案的时候强制类型转换为long long。。
精髓点:
1:j=n/(n/i)
2:已知区间始末和trunc(k/i)时,求k%i的等差数列的和的公式:
∑=(j-i+1)k-(j-i+1)(i+j)/2*(k/i);
#include<cstdio>
#include<iostream>
using namespace std;
int n,k,i,j;
long long ans=0;
int main()
{
scanf("%d %d",&n,&k);
if (n>k)
{
ans+=(long long)(n-k)*k;
n=k;
}
j=0;
for (i=1;i<=n;i=j+1)
{
j=k/(k/i);
if (j>=n)
j=n;
cout<<"j is "<<j<<"i is "<<i;
system("pause");
ans+=(long long)(j-i+1)*k-(long long)(j-i+1)*(i+j)/2*(k/i);
//i代表这一段数的开始位置,j是结束位置.则这一段取mod的结果,
//利用公式k%i=k-trunc(k/i)*i即等于这一段数字的个数*k,
//再减去这一段用k/i的结果(i是首项,j是尾项,j-i+1是项数,利用等差数列进行求和)
}
printf("%lld",ans);
return 0;
}
12 9
j is 1 i is 1请按任意键继续. . .9/1=9..这一段只有一个数
j is 2 i is 2请按任意键继续. . .9/2=4..这一段也只有一个数
j is 3 i is 3请按任意键继续. . .9/3=3..这一段也只有一个数
j is 4 i is 4请按任意键继续. . .9/4=2..这一段也只有一个数
j is 9 i is 5请按任意键继续. . .9/5=1,包括其后的9/6=1,9/7=1,9/8=1,9/9=1.这一段有5个数
39
求约数个数之五
Description
对于输入一个数字,输出其约数个数。
例如10就有4个约数1,2,5,10 。
这种问题,小J已做得非常熟练了
现在老师将这个问题变了下
给出一个数字N,求1到N之间每个数字的约数个数,再输出其累加和
Format
Input
一个数字N,N< =1e14
Output
如题
Samples
输入数据 1
3
输出数据 1
5

#include<bits/stdc++.h>
using namespace std;
long long solve(long long x){
long long L = 1,R = 0;
long long res = 0;
while(L <= x){
R = x/(x/L);
res += (x / L) * (R - L + 1);
L = R + 1;
}
return res;
}
int main()
{
long long n;
cin >> n;
cout << solve(n);
return 0;
}
另一个使用容斥定理求解的程序
Sol:假设n=10,先枚举较小的约数i,i<=sqrt(n)
例如当i=1时,区间[1..10]之内会有10个数字是1的倍数,不妨统设为x,则可以得到下面的式子
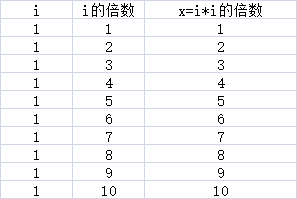
当i=2时,区间[1..10]之内会有5个数字是2的倍数,不妨统设为x,则可以得到下面的式子
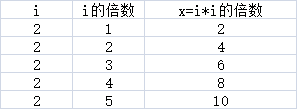
当i=3时,区间[1..10]之内会有3个数字是3的倍数,不妨统设为x,则可以得到下面的式子

于是上面这三个表,就一共有18个形如i*j=x的表达式,在表达式的左边出现了36个数字,它们都为[1..10]之间某个数字的约数
但上表中有些表达式是多余的。
例如
1*1=1
2*2=2
3*3=3
这三个式中的i与j值是一样的,只能算一个,所以另一个要去掉,一共去掉3个,其值为int(sqrt(n))
再例如
2*1=2
3*1=3
3*2=6
这三个式子在整个的18个表达式中,是出现了2次的。
所以这三个式子中的i,j都要去掉。一共去掉6个
用数学公式来表达就是
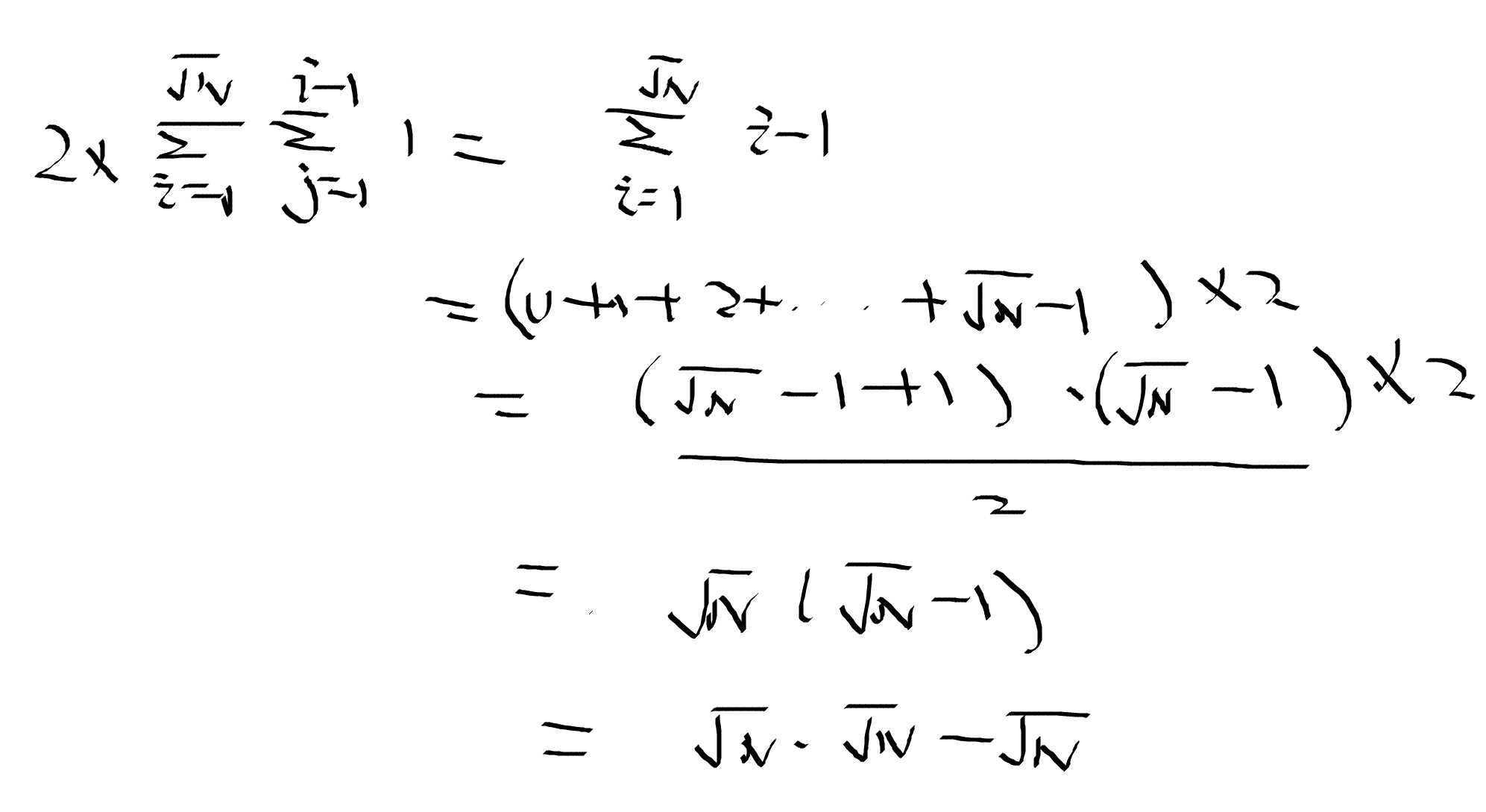
于是所有要去掉的约数个数=int(sqrt(N))+int(sqrt(N))*int(sqrt(N))-int(sqrt(N))=int(sqrt(N))*int(sqrt(N))
.
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,sum=0;
cin>>n;
for(int i=1;i<=n/i;i++)
sum=sum+n/i;
cout<<sum*2-(long long)sqrt(n)*(long long)sqrt(n)<<endl;
return 0;
}
如果使用欧拉筛法来做,时间复杂度为O(N)
#include <iostream>
using namespace std;
const int n = 1e7;
const int N = n + 1;
int m=0;
int a[N], b[N], c[N], d[N];
int f[N], g[N];
void init()
{
f[1] = g[1] = 1;
for (int i = 2; i <= n; i++)
{
if (!a[i])
//如果i不是质数的话,加入质数队列
{
b[++m] = i;
//队列中第m个质数为i
c[i] = 1, f[i] = 2;
}
for (int j = 1; j <=m && b[j] * i <= n; j++)
//枚举质数队列,从小到大
{
int k = b[j];
a[i * k] = 1;
//标记i*k不是质数
if (i % k == 0)
//如果k是i最小的质因子的话
{
c[i * k] = c[i] + 1;
//指数增加1
f[i * k] = (f[i] / (c[i]+1))* (c[i * k] + 1);
//约数个数变化,详见图1
break;
}
else
{
c[i * k] = 1;
//k做为i*k的最小质因子,现在出现了1次
f[i * k] = 2 * f[i];
//约数个数发生变化
}
}
}
}
int main()
{
init();
int x;
cin>>x;
int ans=0;
for (int i=1;i<=x;i++)
ans=ans+f[i];
cout<<ans<<endl;
return 0;
}
求约数之和4
给出一个数字N,求其约数之和是个比较简单的问题
例如N=6时,其约数之和为1+2+3+6=12.
现在给你两个数字a,b
求a,b之间所有数字的约数之和,再累加求和
Format
Input
一行给出a,b
a<=b<=2e9
Output
如题
Samples
输入数据 1
2 4
输出数据 1
14
Sol:明显对于1到N之间的数字,其约数范围也为1到N这个范围内。
于是我们可以枚举约数L,于是N/L就代表1到N之间有多少个数字是L的倍数,L也必为它们的约数。
例如当L=7时,N=20时
N/20=2,说明1到20以内有两个数字是7的倍数,易知为7,14,也就是说在算7和14的约数之和时,必然要将7统计进去。
然后这个算法高明的地方在于
当L=8,9,10时,N/L=2
于是这一段的L=7,R=10
于是这一段的约数之和为2*7+2*8+2*9+2*10=2*(7+8+9+10)=2*(7+10)*(10-7+1)/2
下图中最后一行公式有误 。

#include<bits/stdc++.h>
using namespace std;
long long solve(long long n)
{
long long L = 1,R = 0;
long long res = 0;
while(L <= n){
R = n/(n/L);
res += n / L * (L + R) * (R - L + 1) / 2;
L = R + 1;
}
return res;
}
int main()
{
long long a,b;cin >> a >> b;
cout << solve(b) - solve(a-1);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号