叹息之墙详细版

 

关于点与线段的关系，说明如下：

 

首先明确一条线段有N个点，里面只有N-1边

设第1条边，其长度为点2坐标-点1坐标

设第2条边，其长度为点3坐标-点2坐标

于是我们给某个点i打上标志，则代表由点i与点i+1构成的线段被选中

 

然后我们假设每个点都是可以突破的，但注意试题要我们求的是不可突破的点。

那如何来求呢？

基于下面这个最简单的想法：

如果一段区间[L,R], 如果我们将中间所有的点都突破了的话

则最终获得冲击力为这段区间的长度。

但如果这个冲击力小于左右边界的墙的高度话，那中间的点也白突破了

这一段的长度就要计算在结果当中。

例如下图中

 

 

 

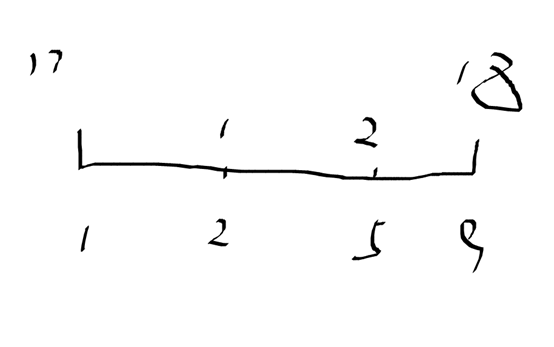
区间［２，５]这一段是可以突破的，因为长度为3，但两边的高度仅为1和2

但整个区间[1,9]长度为8，但两边的高度为17，18，明显突破不了。于是

整个区间要计算在结果当中。

 

这样做的好处在于：

如果我们按高度值进行排序，不断看高的墙所形成的区间，哪些是不能突破的。

则这些区间内部的点是无需再计算的。

于是我们将输入数据将高度进行降序排列

由于高度值是有可能相等的，并且排序后，点的顺序就打乱了。

但每个点的坐标值是互不相同的,并且坐标值巨大啊！

于是我们要建立一个映射，从坐标到点的顺序

例如，在上图中坐标值为1的点，是坐标轴上从左到右第1个点

坐标值为2的点，是坐标轴上从左到右第2个点

坐标值为5的点，是坐标轴上从左到右第3个点

坐标值为9的点，是坐标轴上从左到右第4个点

接下来，我们按权值从大到小进行枚举

 

当枚举到一个点，我们是知道它的高度与坐标值，但注意此时是不能直接得到

这些点在坐标轴的顺序的，必须通过刚才建立的map映射才知道。

将这些点的坐标放入一个set 中

先放入高度为18，加入set后，只有它一个点，即它的左右都没有点，所以什么也不做

再放下高度为17的点，加入set，此时发现在它的右边有点。

想一下，如何确保知道一个点的左边有点，或者右点有点

这个高度为17的点，它左边就没有点哟

对于一个集合的访问，一定要注意不要访问到无效的地址上。

于是取同这两个点的坐标值，差值为9-1=8

并且这个8是小于我们刚才加入的点的高度值17的。

这就说明这两者之间的所有点都是不能被突破的

此时根据坐标值到点的顺序这个映射，得到

高度为17的点，是坐标轴上第1个点

高度为18的点，是坐标轴上第4个点

于是这两个点之间的所有点即1，2，3这3个点，及它们代表的线段均是不可突破的。

 

接下来加入高度为2的点，发现这个点已打了不可突破的标志，所以不用管了

接下来加入高度为1的点，发现这个点已打了不可突破的标志，所以不用管了

 

最终统计结果

发现1这个点打了标志，于是点1到点2的距离要加入

发现2这个点打了标志，于是点2到点3的距离要加入

发现3这个点打了标志，于是点3到点4的距离要加入

 

接下来请同学们画一下这个样例的过程

 

 

 

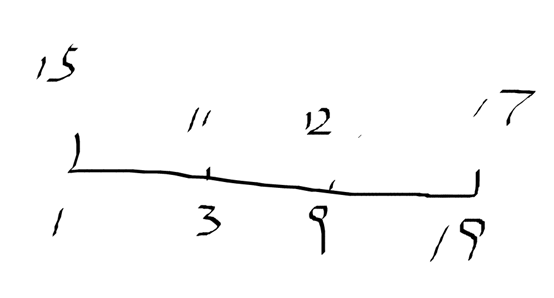
其实这个做法还是有点难想的，而下面这个做法就清爽多了

按坐标从小到大排序

然后对于第i条线段[L,R]，看能不能突破，所谓突破满足两个条件

1：这一段左边的高度<L与R的距离差

2：L点的左边那个点，被打上过突破的标志，这样才说明它逃出来了。

于是f[0]及f[N]要事先打上被突破的标志。这样在求第一段的时候，如果满足条件1，再加上f[0]已是突破状态，于是f[1]也就突破了。

当然也有可能没满足条件1，但在求第二段的时候，因为距离的累加，于是满足条件1了，于是第一段也就突破了。