拓扑排序入门

最长路

给你一个有向无环图，N个点M条边

求最长路

Format
Input
第一行给出N，M，代表点数与边数

接下M行，每行3个数字a,b,c代表从a到b有边权为1

N,M<=1e5

Output
如题 ，如果没有的话，输出0.

否则输出结果%10^9+7

Samples
输入数据 1
4 5
1 2
1 3
3 2
2 4
3 4
输出数据 1
3

 

这个权值在边上

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

#include<bits/stdc++.h> using namespace std; const int mod=1e9+7; int n,m; int x,y; int dep[100010]; int son[2000010],now[2000010],pre[2000010],val[2000010],tot; queue<int> q; int ans; void put(int x, int y) {     pre[++tot] = now[x];     now[x] = tot;     son[tot] = y; } int main() {     cin>>n>>m;     //n个点,m条边     for(int i=1; i<=m; i++)     {         cin>>x>>y;         put(x,y);         dep[y]++;         //y的入度加1     }     for(int i=1; i<=n; i++)         if(dep[i]==0)         //将入度为0的点加入队列             q.push(i);     tot=0;     while(!q.empty())     //当队列不为空     {         int noww=q.front();         //取出头结点         q.pop();         tot++;         for(int i=now[noww]; i; i=pre[i])         //遍历与noww相连的边，找出这条边上的另一个点         {             dep[son[i]]--;             //son[i]这个点的入度要减少1             if(dep[son[i]]==0)                 q.push(son[i]);             val[son[i]]=max(val[son[i]],val[noww]+1);         }     }     if(tot!=n)        cout<<0<<endl;     else     {         for(int i=1; i<=n; i++)             ans=max(ans,val[i]);         cout<<ans%mod<<endl;     }       return 0; }

　　

 

Test for Job

Mr.dog被他原来的公司炒了。现在为了养家糊口的他，要尽快找到一个工作。现在有一个工作，但是这年头失业的人很多啊，因此公司不得不使用一个测试来选择自己需要的职工。

这个测试是这样的：从一个起始的城市出发，通过单向的路径来到其他的城市，并且经过每个城市可能会赚到一定的利润，或者交纳一定的费用，这样不断的行动，直到到达一个终点的城市。你的老板会在终点处等你，他会总结出你一路上花费的费用，或者是得到的利润，来决定你是否能够被雇佣。

为了更好的得到这份工作，Mr.dog设法得到了所有城市经过的纯利润Vi（如果是负数表示到这个城市不但得不到利润，还要花费），以及城市与城市的连通关系。假设一个城市没有能够从其他城市到达的道路，那么这个城市被看作起始的城市之一；假设一个城市没有能够到达其他城市的道路，那么这个城市被看作终点的城市之一；而Mr.dog的任务是将选择一个起始的结点出发，走出一条路径，这条路径在一个终点的城市结束，且这条路径包含的城市的总利润最大。

Input
包含若干个数据。

每个数据的第一行有2个整数n,m(1 < = n < = 100000,1 < =m < = 1000000)

后面紧接着n行，其中第i行描述Vi

再后面紧接m行，第i行2个整数x,y，表示有一条从x到y的单向道路。

数据保证没有点对（x,y）重复出现，并且保证无法从一个城市出发经过若干条路径后再回到这个城市。

Output
只有一行，一个整数表示dog这次测试最多可以得到多少利润（或者说最少使用多少花费）

Samples
输入数据 1
6 5
1
2
5
2
1
1
1 2
1 3
2 4
3 4
5 6
输出数据 1
8

Hint
请用 while(scanf("%d%d",&n,&m)!=EOF)进行读入

 

 

 这个权值在点上

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

#include<bits/stdc++.h> using namespace std; int n,m; int x,y; int dep[2000010],out[2000010],val[2000010],ans[2000010]; int son[2000010],now[2000010],pre[2000010],tot; queue<int> q; int max1; void put(int x, int y) {     pre[++tot] = now[x];     now[x] = tot;     son[tot] = y; } int main() {     while(scanf("%d%d",&n,&m)!=EOF) {         memset(dep,0,sizeof dep);         memset(son,0,sizeof son);         memset(now,0,sizeof now);         memset(pre,0,sizeof pre);         memset(val,0,sizeof val);         memset(ans,0,sizeof ans);         memset(out,0,sizeof out);         tot=0;         for(int i=1; i<=n; i++) cin>>val[i],ans[i]=-INT_MAX;         for(int i=1; i<=m; i++) {             cin>>x>>y;             put(x,y);             dep[y]++;             out[x]++;         }         for(int i=1; i<=n; i++)             if(dep[i]==0)                 q.push(i),ans[i]=val[i];         while(!q.empty()) {             int noww=q.front();             q.pop();             for(int i=now[noww]; i; i=pre[i]) {                 dep[son[i]]--;                 if(dep[son[i]]==0)                     q.push(son[i]);                 ans[son[i]]=max(ans[son[i]],ans[noww]+val[son[i]]);                 //已找到一条路径了，于是更新下最值优                 //这个与是否入度为0，是没有关系的             }         }         max1=-INT_MAX;         for(int i=1; i<=n; i++)             if(out[i]==0)                //找到出度为0的点，其代表终点                 max1=max(max1,ans[i]);         cout<<max1<<endl;     }       return 0; }

　　

 

有限制的全排列

给你一个数字N，及另一个数字M

代表希望你找出N的某个全排列出来，其满足M个条件

每个条件会给出两个数字a,b

代表在目标全排列中，数字a在数字b前面

Format
Input
第一行两个整数n,m

接下来M行，每行两个数字

Output
输出目标全排列，找不到输出-1

如果存在多个解则输出字典序最小的那个

Samples
输入数据 1
4 3
2 1
3 4
2 4
输出数据 1
2 1 3 4

 

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

#include<bits/stdc++.h> using namespace std; int n,m; int x,y; int dep[2000010]; int son[2000010],now[2000010],pre[2000010],tot; priority_queue<int, vector<int> , greater<int> > q; queue<int> ans; void put(int x, int y) {     pre[++tot] = now[x];     now[x] = tot;     son[tot] = y; } int main() {     cin>>n>>m;     for(int i=1; i<=m; i++) {         cin>>x>>y;         put(x,y);         dep[y]++;     }     for(int i=1; i<=n; i++)         if(dep[i]==0)             q.push(i);     while(!q.empty()) {         int noww=q.top();         q.pop();         ans.push(noww);         for(int i=now[noww]; i; i=pre[i]) {             dep[son[i]]--;             if(dep[son[i]]==0) q.push(son[i]);         }     }     if(ans.size()!=n) cout<<-1<<endl;     else {         while(!ans.empty()) cout<<ans.front()<<" ",ans.pop();         cout<<endl;     }       return 0; }

　　

 

有限制的全排列

 

给你一个数字N，及另一个数字M

 

代表希望你找出N的某个全排列出来，其满足M个条件

 

每个条件会给出两个数字a,b

 

代表在目标全排列中，数字a在数字b前面

 

Format

Input

第一行两个整数n,m

 

接下来M行，每行两个数字

 

Output

输出目标全排列，找不到输出-1

 

如果存在多个解则输出字典序最小的那个

 

Samples

输入数据 1

4 3

2 1

3 4

2 4

输出数据 1

2 1 3 4

 

sol:

针对形如

a要放在b的前面的表述，建立一条有向表从a指向b

 

然后找出所有入度的0的点，放入一个小根堆中（注意不是一般的队列）

 

然后不断从堆中弹出堆顶元素x，其权值最小，并且是比所有数字小的。

 

然后将所有与x相连的边所指向的另一个点的入度减少1，如果入度为0，则又放到小堆根中，最终得到答案

 

针对样例来说：

2 1

3 4

2 4

 

建立的图形如下：

 

 

 

 

 

 

 

 

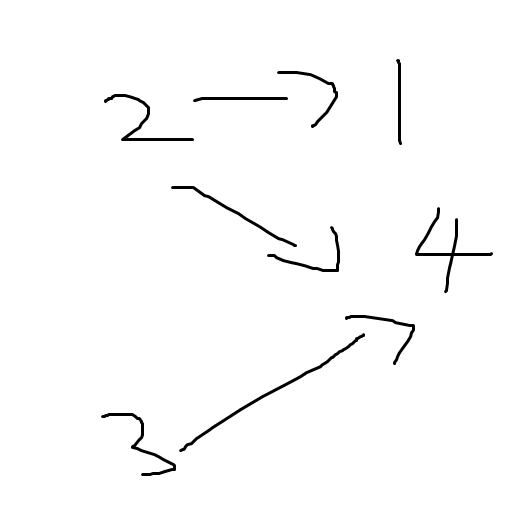
首先将入度为0的点2，3入堆中

 

然后弹出2出，并将1与4的入度分别减少1。发现1的入度为0，于是1进入堆中

 

然后弹出1，1没有相连的边，无后续操作

 

然后弹出3，将4的入度减少1，发现4的入度为0，加入堆中

 

最后弹出4

 

最终结果为2，1，3，4

 

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

#include<bits/stdc++.h> using namespace std; int n,m; int x,y; int dep[2000010]; int son[2000010],now[2000010],pre[2000010],tot; priority_queue<int, vector<int> , greater<int> > q; queue<int> ans; void put(int x, int y) {     pre[++tot] = now[x];     now[x] = tot;     son[tot] = y; } int main() {     cin>>n>>m;     for(int i=1; i<=m; i++) {         cin>>x>>y;         put(x,y);         dep[y]++;     }     for(int i=1; i<=n; i++)         if(dep[i]==0)             q.push(i);     while(!q.empty()) {         int noww=q.top();         q.pop();         ans.push(noww);         for(int i=now[noww]; i; i=pre[i]) {             dep[son[i]]--;             if(dep[son[i]]==0) q.push(son[i]);         }     }     if(ans.size()!=n) cout<<-1<<endl;     else {         while(!ans.empty()) cout<<ans.front()<<" ",ans.pop();         cout<<endl;     }       return 0; }

　　

 

 

小球的标签

 

有N个球，重量从1到N，各不相同，每个球有个编号也是从1到N，各不相同。现在给你一些约束条件， 每个约束条件给出数字A,B,表示A号球轻于B号球。请你求出满足约束条件的某个球的重量的全排列， 注意如果有多个排列满足条件，我们希望1号球的重量越小越好;当1号球的重量一样时，希望2号球的重量越小越好 当2号球的重量一样时，希望3号球的重量越小越好

 

Input
第一行给出一个数字N，代表有N组数据

 

每个数据给出数字N，M，代表有N个球，

 

M个约束条件N (1 ≤ N ≤ 200) , M (0 ≤ M ≤ 40,000).

 

下面将有M行每行两个数字A,B，(1 ≤ a, b ≤ N)表示A号球轻于B号球.

 

Output
依次输出从1号球到N号球的重量,任两个数字之间以一个空格格开

 

无解输出-1

 

Sol:
本题要求最终结果字典序最小，有两种策略
1：将较轻的重量给数字编号较小的球
2：将较重的重量给数字编号较大的球

 

发现策略2优于策略1，例如下面这组数据
4 2
3 1
2 4
我们建立有向边a-->b,代表a重于b,上图形如下

 

 

 

 

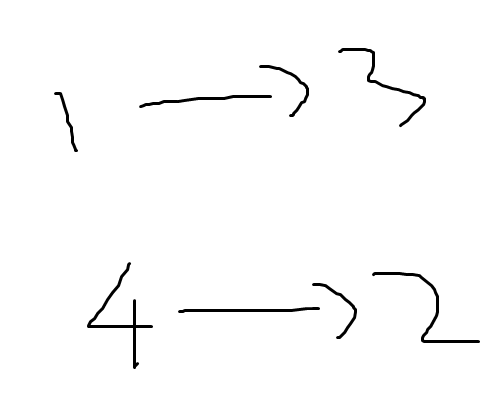
将1与4进大根堆

 

弹出4，将最大的重量4给它，然后将2加入堆

 

弹出2，将重量3给它

 

弹出1，将重量2给它，然后3加入堆

 

最后弹出3，将重量1给它。

 

最终1，2，3，4这四个球的重量分别为2 3 1 4

 

 

大家可试用着策略1来做一下，发现结果并不优于这种

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71

#include<cstdio> #include<cstring> #include<algorithm> #include<queue> using namespace std; int head[500],degree[500],result[450],m,n,t; struct node {     int to,next; }s[400000]; void add(int x,int y) {     s[t].to=y;     s[t].next=head[x];     head[x]=t++; } int topo() {     int i,j,p;     priority_queue<int >Q;     for(i=1;i<=m;i++)     if(degree[i]==0)     Q.push(i);     p=m;     while(!Q.empty())     {         int w=Q.top();         Q.pop();         result[w]=p--;                    for(int k=head[w];k!=-1;k=s[k].next)         {             int e=s[k].to;             degree[e]--;                            if(!degree[e])             Q.push(e);         }     }     if(p==0)     return 1;            return 0; } int main() {     int N,a,b,i,j;     scanf("%d",&N);     while(N--)     {         t=0;         memset(degree,0,sizeof(degree));         memset(head,-1,sizeof(head));         scanf("%d%d",&m,&n);         for(i=0;i<n;i++)         {             scanf("%d%d",&a,&b);             add(b,a);             degree[a]++;         }         int qw=topo();         if(qw)         {             for(i=1;i<m;i++)             printf("%d ",result[i]);             printf("%d\n",result[i]);         }         else         printf("-1\n");     }     return 0; }