guruguru
# Description
有一个转盘, 如下图, 转盘上等分成m个刻度, 依次顺时针编号
1∼ m 。 转盘上有两个按钮, 一个为黑色, 一个为红色, 按动黑
色按钮一次转盘上的指针会顺时针转动一格, 按动红色按钮一次
转盘上的指针会顺时针转动到我们事前确定的刻度 x.
我们有一组长度为 n 的序列 a[1],a[2],…,a[n]。 起始时指针停在刻
度 a[1], 现在我们需要按动两个按钮使指针依次到达 a[2],a[3],…,a[n]。
请编程输出事前确定的刻度 x 为多少时? 按动按钮的次数最少。
# Format
## Input
第一行给出N ,M
第二行给出N个数字
## Output
输出事前确定的刻度 x 为多少时? 按动按钮的次数最少。
# Samples
```input1
4 6
1 5 1 4
```
```output1
5
```
Sol:
先考虑最简单的情况,从a[i]到a[i+1],并且a[i+1]>a[i],例如从位置3到位置8.
易知如果没有红色的按钮的话,就只能使用黑色按钮。则按a[i+1]-a[i]次,就可以从a[i]档到a[i+1]档。
如果有红色按钮,可以一步跳到x位置,则假如x设置在其中间位置,只需按a[i+1]-x+1次即可完成任务。那么可以将每个a[i]和a[i+1]看成一条线段,只要x设置在线段上,这次操作就有相应的次数减少,减少的次数为x-a[i]-1次,x在线段外即对当前操作无影响。
注意到这个影响量x-a[i]-1,由两部分组成,其中x是个变化的量,a[i]+1是个稳定的量。将后者提取出来,设一个b数组将线段上区间为[a[i-1]+1,a[i]]这一段,都加上权值a[i]+1(这个权值是今后算最终结果时,要减去的部分),同时另开数组c在同样线段上各个值+1,表示x设这个位置就能减少次数,最后遍历一下就能知道x设置在位置i能减少的总次数了,上述操作用差分数组解决,复杂度O(n)。
再考虑复杂一点的情况,即a[i]>a[i+1],即从位置8到位置3的话.
如果x设在位置1,2的话,则按前面所算的减少次数
x-a[i]-1这个值为负数不合法了。
由于点呈环形,所以1号点,也就相当于M+1点,2号点相当于M+2点
所以减少次数应该为x+m-a[i]-1,即为x-(a[i]+1-m)
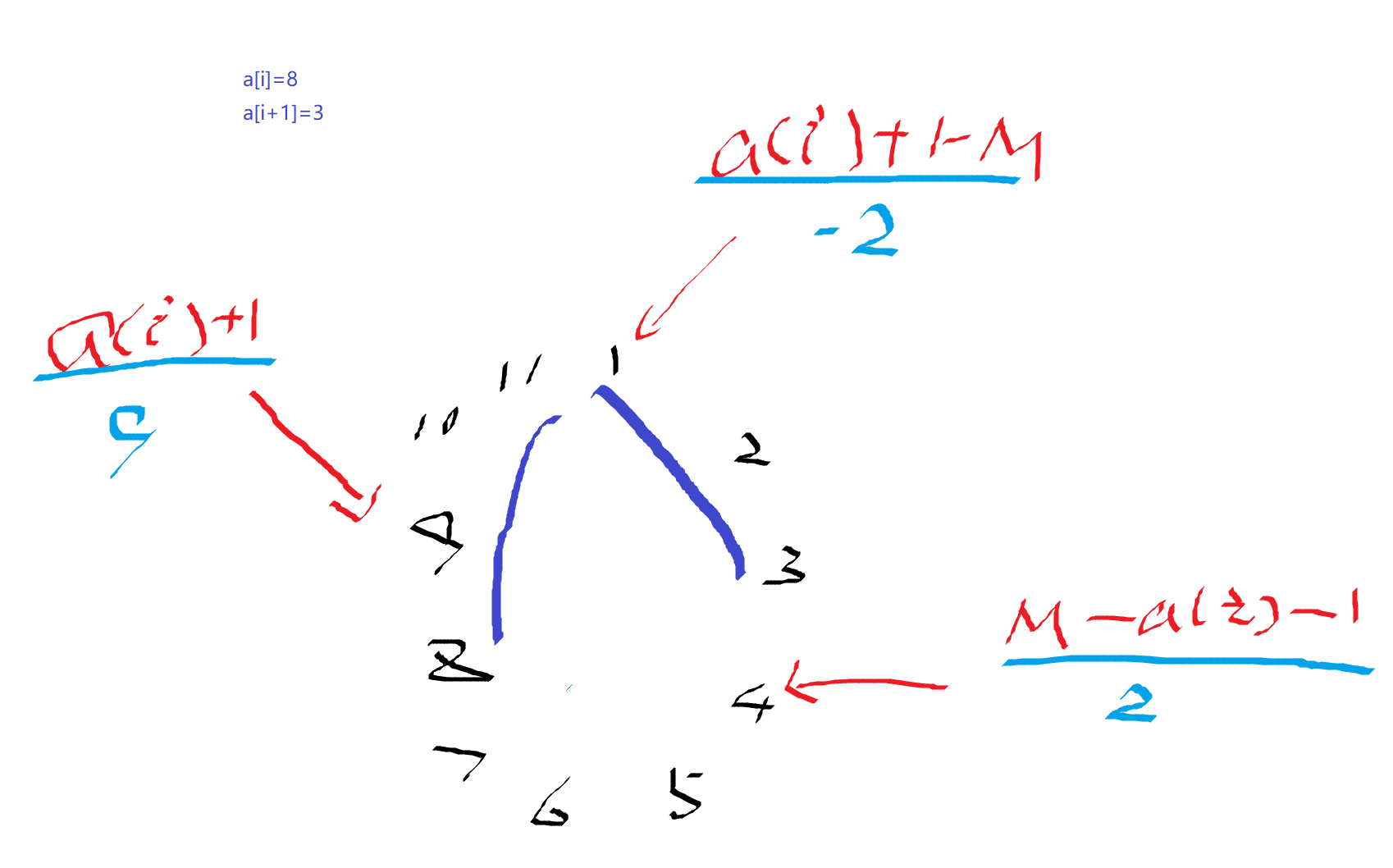
将8到3这一段,分成8到11,1到3这一段
分别给9,1,4这3个点打上标志,如下图所示。
1那个点打的标志,有点奇怪,是个-2,其实这个是对的。
因为当x=1时,1-(-2)=3,即减少3步,如果是直接走的话,要6步,现在就只要6-3=3步了。
当x=2时,2-(-2)=4,即减少4步,如果是直接走的话,要6步,现在就只要6-4=2步了。
9那个点上,打的值为9,于是当x=9时,9-9=0,也正好说明转移门设在9那个位置是没有改变的。
# include <bits/stdc++.h> using namespace std; typedef long long LL; const int maxn = 1e5; LL a[maxn+3]={0}, b[maxn+3]={0}, c[maxn+3]={0}; int main() { LL sum = 0; int n, m; scanf("%d%d%lld",&n,&m,&a[1]); for(int i=2; i<=n; ++i) { scanf("%lld",&a[i]); if(a[i] > a[i-1]) { sum += a[i]-a[i-1]; b[a[i-1]+1] += a[i-1]+1; b[a[i]+1] -= a[i-1]+1; ++c[a[i-1]+1]; --c[a[i]+1]; } else
//这个逆的标志怎么打的啊。。。。。。。。。 { sum += m-a[i-1]+a[i]; b[a[i-1]+1] += a[i-1]+1; ++c[a[i-1]+1]; b[1] -= m-a[i-1]-1; ++c[1]; b[a[i]+1] += m-a[i-1]-1; --c[a[i]+1]; } } for(int i=1; i<=m; ++i) b[i] += b[i-1], c[i] += c[i-1]; LL ans = 0; for(int i=1; i<=m; ++i) ans = max(ans,i*1LL*c[i]-b[i]); printf("%lld\n",sum-ans); return 0; }
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1000005
using namespace std;
typedef long long ll;
inline int read(){
int sum = 0, t = 1; char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') t = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9'){ sum = sum * 10 + ch - '0'; ch = getchar(); }
return sum * t;
}
int n, m;
int a[N];
ll d[N], Ans;
int main(){
n = read(); m = read();
for(int i = 1; i <= n; i++)
a[i] = read();
for(int i = 1; i < n; i++)
if(a[i] < a[i + 1]){
d[a[i] + 2]++;
d[a[i + 1] + 1] -= a[i + 1] - a[i];
d[a[i + 1] + 2] += a[i + 1] - a[i] - 1;
Ans += a[i + 1] - a[i];
}
else {
d[a[i] + 2]++;
if(a[i] < m) d[1] += m - a[i], d[2] -= m - a[i] - 1;
else d[2]++;
d[a[i + 1] + 1] -= a[i + 1] - a[i] + m;
d[a[i + 1] + 2] += a[i + 1] - a[i] + m - 1;
Ans += a[i + 1] - a[i] + m;
}
for(int i = 1; i <= m; i++)
d[i] += d[i - 1];
for(int i = 1; i <= m; i++)
d[i] += d[i - 1];
ll S = 0;
for(int i = 1; i <= m; i++) S = max(S, d[i]);
printf("%lld\n", Ans - S);
}



